基于压缩感知测量值的宽带雷达回波信号NP检测
张晓伟 杨咚咚
(陕西黄河集团有限公司设计研究所 西安 710043)
0 引言
近年来,由Candès, Romberg, Tao[1]和Donoho[2]等人提出的压缩感知(Compressed Sensing, CS)新理论,打破了传统的乃奎斯特采样定理,在雷达[3]、检测与估计[4]和SAR成像[5]等领域得到广泛应用。CS理论指出:当信号在某个基空间(词典)中稀疏时,可以低于传统乃奎斯特采样率,以较低码率采样信号,而不丢失信号信息。在宽带雷达背景下,目标回波信号是发射信号和目标脉冲响应函数的卷积,表现为一维距离像。脉冲响应函数和目标的散射点有关,而其散射点的个数是有限个,在由发射信号及其时延、调制等构成的基空间中,宽带雷达回波信号是稀疏的,可以低码率采样,而不丢失目标信息。雷达的基本功能之一就是实现目标的检测,奈曼-皮尔逊检测(Neyman-Pearson Detection, NPD)准则是雷达、声纳等目标检测最基本、最重要的准则之一。文献[6]提出了雷达回波信号与由发射信号构成的基空间中的基向量做相关运算,其本质上是匹配滤波。文献[7]提出了在CS背景下,构造与发射信号匹配的字典,以低码率采样回波信号,实现回波信号的重构检测目标的方法,但是该算法要求重构雷达回波信号,具有较大的运算量。
本文提出了基于CS测量值的宽带雷达回波信号奈曼-皮尔逊检测(Neyman-Pearson Detection Based on Compressed Sensing measure-ments,NPDBCS)准则。该准则直接选取宽带雷达回波信号的CS测量值作为检验统计量,在给定虚警概率时,依据贝叶斯判定准则得到检测概率,并将其推广到多元假设检测。在测量矩阵为高斯矩阵和伯努利矩阵时,基于实测的宽带雷达回波信号实验结果验证了该准则的可行性,NPDBCS准则可以用较少的测量值实现目标有效检测,而不需要重构雷达回波信号。
1 NPDBCS准则
1.1 CS基本原理

(1)
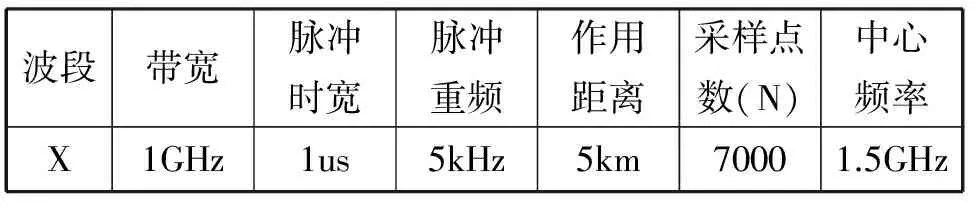
其中Θ∈RN为X在基空间Ψ中投影N×1维的系数矩阵,ψi为基空间Ψ第i个基向量,θi为信号X由基向量ψi线性表示的相关系数。X是信号的时域表示,为X的Ψ域表示。在投影系数矩阵Θ中,如果θi的非零个数K远远小于N(K< (2) 文献[8]指出,对于K稀疏的信号X,可以通过一个满足有限等距特性(Restricted Isometry Property, RIP)的测量矩阵Φ测量,通过求解一个最优化式(3),以相当高的概率重构原信号X: min||Θ||0,s.t.Y=ΨX=ΦΨΘ=ACSΘ (3) 其中||Θ||0为Θ的零范数;ACSΘ为CS测量矩阵,由于式(3)为组合优化问题,直接求解很困难。Donoho指出可以将问题(3)转化为L-1范数,通过求解一凸优化求解: min||Θ||1,s.t.Y=ΨX=ΦΨΘ=ACSΘ (4) 利用此方法可以几乎完美的重构原信号X,线性测量矩阵Φ可以选取高斯矩阵、伯努利矩阵等,对于测量次数M则必须满足M≥O(Klog(N/K))。CR=N/M>1称为压缩比,对于一个N×1维信号X,可以由M(M< 由发射信号及其时延、调制等构成的基空间,宽带雷达回波信号可以由其基空间中的基向量稀疏表示。由CS理论可知,回波信号可以以低于乃奎斯特采样率采样,而不丢失目标信息,实现回波信号的重构。我们可以直接选取宽带雷达回波信号的CS测量值作为检验统计量,建立NPDBCS准则,实现目标检测而不需要重构回波信号。在假设H0时,只包含高斯白噪声的测量值,在假设H1时,包含信号和高斯白噪声的测量值: (5) (6) (7) 设定检测门限λ,由贝叶斯判定准则得: (8) 将式子(6)和(7)代入(8),化简得: (9) (10) 则我们可以分别得到检测概率PD和虚警概率Pf: (11) (12) (13) 在上式中,如果测量矩阵Φ每一行都相互正交,则ΦΦT=IM,PD可简化为: (14) 在文献[9]中,Richard等从Johnson-Lindenstrauss引理出发,指出对于高斯矩阵和伯努利矩阵有下面定理成立:对于稀疏信号X={x1,x2,...,xN}∈RN×1,其非零元素个数为K< (15) 对于式(14)而言,当δ足够小时,检测概率PD可写成: (16) 当虚警概率Pf相等时,比较NPD准则和NPDBCS准则得到检测概率PD: (17) (18) 实验选取实测的宽带雷达回波信号,在测量矩阵为高斯矩阵和伯努利矩阵时,对NPD和NPDBCS两种准则进行检测比较。所选取回波信号的宽带雷达系统部分参数如表1所示,图1为所选取目标回波信号的波形和经过匹配滤波器的脉压结果,从图1中可以看出所选取的回波信号信噪比较高,可近似认为回波信号不包含噪声。将回波信号进行归一化,加入高斯白噪声,给定恒定虚警概率,在不同CR和SNR时,分别选取高斯矩阵和伯努利矩阵作为测量矩阵对两种检测准则进行比较,实验1和2分别为高斯矩阵和伯努利矩阵时基于NPDBCS准则的实测回波信号检测实验;实验3为两种测量矩阵基于NPDBCS准则的实测回波信号检测比较实验;实验4为基于NPD和NPDBCS准则实测回波信号检测比较实验。 表1宽带雷达系统的部分参数 波段带宽脉冲时宽脉冲重频作用距离采样点数(N)中心频率X1GHz1us5kHz5km70001.5GHz 实验1:高斯矩阵 实验1为所选取测量矩阵为高斯矩阵,给定恒定虚警概率,比较在不同CR和SNR时NPDBCS检测性能。设置Pf=0.1,当CR=10,20,50,100时,1000次蒙特-卡罗实验时NPDBCS准则检测比较。对于式(11)和(16)所对应测量矩阵行向量未正交化和正交化两种情况。图3为蒙特-卡罗实验所得到四种CR和不同SNR时,所得到NPDBCS准则检测概率,表2为实验参数。 表2高斯矩阵实验参数 NCRKPf700010205010010000.1 表3检测概率为1所要求的最小信噪比 CR102050100SNR/dB-14.11-11.03-6.799-2.427 从图2可知,在不同CR和SNR时,行向量未正交化和正交化的高斯矩阵其检测性能基本一致。在给定Pf=0.1,不同CR时,PD达到1所需要的SNR最小,如表3所示。实验结果表明:当测量矩阵为高斯矩阵,在恒定Pf时,CR越大,PD达到1所需要的SNR也越高。 实验2:伯努利矩阵 对于伯努利矩阵,选取和高斯矩阵相同的实验参数,如表格2所示。图3为当测量矩阵为伯努利矩阵时,1000次蒙特-卡罗实验在不同CR和SNR时所得到的NPDBCS准则检测概率。 从图3可知,和高斯矩阵一样,在不同CR和SNR时,行向量未正交化和正交化的伯努利测量矩阵二者检测性能基本一致。在Pf=0.1,不同CR时,PD达到1时所需要的SNR最小,如表4所示。实验结果表明:和高斯矩阵一样,当测量矩阵为伯努利矩阵,在恒定Pf时,CR越大,PD达到1所需要的SNR也越高。 从图2和3可知,不管测量矩阵是高斯矩阵还是伯努利矩阵, NPDBCS准则完全可以用较少的测量值实现目标检测;当Pf相等时,随着CR的增大,PD达到1时所需要的SNR越高;对于行向量未正交化和正交化的两种测量矩阵,当SNR相等时,二者的检测效果基本一致,并无太大差异。 表4检测概率为1所要求的最小信噪比 CR102050100SNR/dB-14.12-11.03-6.933-1.979 实验3:两种测量矩阵比较 为了比较高斯矩阵和伯努利矩阵时,NPDBCS准则的检测效果,选取和实验1、2相同的实验参数。当Pf=0.1,CR=10,20,50,100时,行向量未正交化和正交化的高斯矩阵和伯努利矩阵四种情形下,1000次蒙特-卡罗实验时NPDBCS准则检测效果基本相同,并无太大差异,如图4所示。其中NG和NB分别表示行向量未正交化的高斯矩阵和伯努利矩阵,G和B分别表示行向量正交化高斯矩阵和伯努利矩阵。 实验4:两种检测准则的比较 由实验1和2可知,对于行向量未正交化和正交化的高斯矩阵和伯努利矩阵这两种测量矩阵,基于NPDBCS准则检测性能基本一致,因此只选取行向量未正交化的高斯矩阵和伯努利矩阵进行比较NPD和NPDBCS准则。选取实验1中宽带雷达回波信号,分别设Pf=0.01,0.05,0.1,0.2,CR=2,10,20比较两种检测准则,实验参数如表5所示。行向量未正交化的高斯矩阵和伯努利矩阵的NPDBCS准则和传统的NPD准则1000次蒙特-卡洛实验检测概率分别如图5和6所示,其中G表示高斯矩阵,B表示伯努利矩阵;表6和7分别为高斯矩阵和伯努利矩阵时,当Pf和CR相同时,基于NPDBCS和NPD准则PD达到1所需要最小SNR。 表5比较两种准则的实验参数 NCRKPf70002102010000.010.050.10.2 从图5和6可知,给定Pf,当PD小于1且SNR相等时,传统的NPD准则检测性能优于NPDBC准则;随着CR和Pf的增大,传统NPD准则和NPDBCS准则PD达到1所要求的SNR都逐渐变大;从表7和8可知,当Pf相等时,传统的NPD准则PD达到1时所要求的SNR低于NPDBCS准则;对于NPDBCS准则,CR越大,PD达到1所要求的SNR就越大。 NPD准则和NPDBCS准则其本质是基于信号能量检测,对于传统的NPD准则,其信号本身没有压缩,而对于NPDBCS准则,虽然保留了信号信息,但是由于CR不小于1,其信号能量有所减少,其优势在于用较少的CS测量值实现目标的检测,而NPD准则不具有这样的优势。 表6高斯矩阵时最小信噪比比较 NPDBCSNPDCR=2CR=10CR=20Pf=0.01-19.55dB-12.48dB-9.444dB-22.57dBPf=0.05-20.57dB-13.22dB-9.501dB-23.48dBPf=0.1-21.15dB-13.85dB-9.575dB-24.45dBPf=0.2-22.57dB-23.48dB-24.45dB-25.03dB 表7伯努利矩阵时最小信噪比比较 NPDBCSNPDCR=2CR=10CR=20Pf=0.01-19.56dB-12.02dB-9.555dB-22.57dBPf=0.05-20.57dB-13.32dB-9.299dB-23.48dBPf=0.1-21.15dB-13.87dB-11.07dB-24.45dBPf=0.2-21.93dB-14.86dB-11.13dB-25.03dB 奈曼-皮尔逊检测准则是雷达、声纳等目标检测最基本、最重要的准则之一。本文提出的基于CS测量值的宽带雷达回波信号NPD准则,它直接选取回波信号的CS测量值作为新的检验统计量,在给定虚警概率时,由贝叶斯判定准则得到检测概率,并将其推广到多元假设检测。当测量矩阵为高斯矩阵和伯努利矩阵时,基于实测宽带雷达回波信号实验结果验证了新准则的可行性,它可以用较少的采样值实现目标检测,且不需要重构回波信号,而传统的NPD准则不具有这个特点,这对宽带雷达回波信号检测具有一定意义。 参考文献: [1]Donoho D., Compressed sensing[J]. IEEE Transactions Infor-mation Theroy, 2006, 52(4):1289-1306. [2]Herman M., Strohmer T., High-resolution radar via compressed sensing[J]. IEEE Transactions on Signal Processing, 2009, 57(6): 2275-2284. [3]Herman M., Strohmer T., High-resolution radar via compress-ed sensing[J]. IEEE Transactions on Signal Processing, 2009, 57(6): 2275-2284. [4]Davenport M., Wakin M., and Baraniuk R., Detection and estimation with compressive measurements, [R/OL] http://dsp.rice.edu/cs. [5]张军,王勇,邱万兵,杨磊,郭鹏程.基于极化SAR数据的图像分类识别算法[J],火控雷达技术,2015, 44(4): 55-64. [6]Gao D., Liu D., and Feng Y., etc., Radar echo signal detection with sparse representations[C]. IEEE conference on signal processing systems, 2010. [7]Shi G., Lin J. and Chen X., etc., UWB echo signal detecetion with ultra-low rate sampling based on compressed sensing[J]. IEEE Trans-actions Circuits and Systems-Ⅱ: Express Briefs, 2008, 55(4): 379-383. [8]E. J. Candès and T. Tao, Near optimal signal recovery from random projection: universal encoding strategies?[J]. IEEE Trans-actions Information Theory, 2006, 52(12): 5406-5425.1.2 基于CS测量值的NPD准则
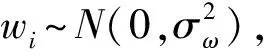



2 宽带雷达回波信号实验






3 结束语

