“倒数曲线”及其在高中数学解题中的应用
郭怡同
“倒数曲线”主要指的是将常见函数或者能画出图像的函数,先取其倒数然后画出图像,因而,可以将所得的图像称为原函数的“倒数曲线”.简单地说,如果从函数表达式上进行分析,其整体为倒数;但从形上进行分析,其函数图像可以依照“倒数曲线”完成.现笔者结合实际学习内容以及高中数学部分基本初等函数对“倒数曲线”进行如下分析.
一、倒数曲线形式
(一)对数函数
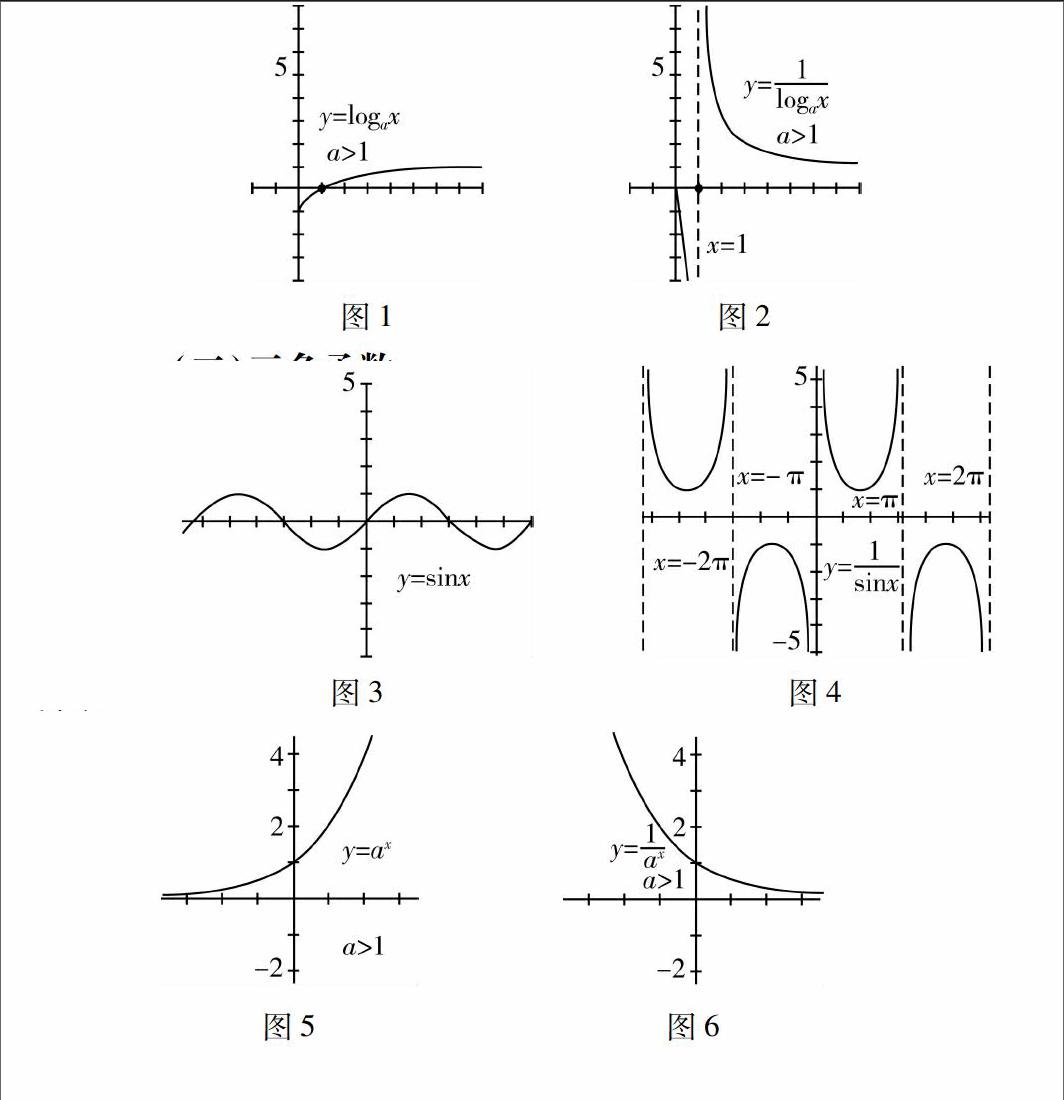
对数函数为y=logax(其中a>0且a≠1)的函数,当a>1时其函数图像如图1所示,设对数函数的倒数为y=1logax(a>1).在对此函数图像进行描绘的过程中,我们应该关注到其中的关键点包括如下三点:① y正数倒数为正数,负数倒数为负数;② 当x→0+时,有y→0-,那么当x→+∞,则有y→0+;③ 由于函数的定义域为(0,1)∪(1,+∞),因而,函数的图像不连续,那么当x→1+时,有y→+∞,那么当x→1-,则有y→-∞.也就是说x=1为渐近线.因而,我们可以将函数y=logax(其中a>1)的倒数曲线画出,如图2所示.
(二)三角函数
在高中数学学习中,三角函数图像更是我们学习的重点.如图3所示为正弦函数y=sinx的图像.在对此函数的倒数y=1sinx的图像进行描绘的过程中,我们应该关注到其中的关键点:① 正数倒数为正数,则可知负数倒数为负数;“1”的倒数为“1”,且“-1”的倒数为“-1”;② 当sinx→0+时,有y→+∞,那么当sinx→0-,则有y=→-∞,如此其图像中便出现渐近线;③ 由于函数的定义域为{x|x≠kπ,k∈Z},因而,函数的图像不连续.因而,我们可以将函数y=sinx的倒数曲线画出,如图4所示.
(三)指数函数
指数函数为形如y=ax(其中a>0且a≠1)的函数,当a>1时其函数图像如图5所示,指数函数的倒数则为y=1ax(a>1).在对此函数图像进行描绘的过程中,关键点包括:① “1”的倒数为“1”;② 当x→+∞时,有y→0+,那么当x→-∞,则有y→+∞;③ 由于函数y的图像不连续,因而,我们可以将函数y(其中a>1)的倒數曲线画出,如图6所示.
(四)复合型函数
对函数进行分析后就不难画出复合型函数倒数曲线,但在画出图像的过程中,我们还应该注意到当原函数值为0时,倒数曲线便会出现渐近线.因而,只有在对原函数最值进行计算后才能掌握倒数曲线关键点坐标.
二、倒数曲线的应用
“倒数曲线”在高中数学解题中占有重要的地位,在对“倒数曲线”进行学习的过程中,应该学会采用数学思想方法.数学思想方法是数学知识在更高层次上的抽象和概括,其知识具有较为明显的策略性.对数学思想方法的渗透,有助于我们理性数学思维能力的提高,从而提高我们对问题进行分析、解决的能力.对不同函数“倒数曲线”分析的过程,是我们进行再发现、再创造活动的探索过程.并且在对不同函数推导其“倒数曲线”图像的过程中渗透分类讨论的思想及数形结合思想,通过详细完整的分类,能够提高我们的讨论意识;而通过图形呈现的方式,有助于我们更好地理解问题的本质.
三、结束语
一部分学生在学习的过程中认为“倒数曲线”的图像分析并不重要,认为重要的是学会在解题的过程中更好地运用公式.但从对不同函数的“倒数曲线”图像分析的过程中发现,图像的分析能够显著地提高我们对不同函数图像的理解.通过图像分析,可以在学习的过程中了解数学也是一种文化,因而,在学习的过程中可以适当地了解数学史知识,从中领悟到数学的美学价值,最终提高自身的数学文化素养.除此之外,在解题的过程中能够更好地应用“倒数曲线”图像,从中能够发现问题的本质,最终提高学生学习效率.

