基于博弈论在需求和产量不确定下的三级供应链协调研究

周荣虎

摘要： 供应链协调是供应链管理中一个重要的研究领域，为了使供应链系统达到整体最优化而又不伤害到供应链中所有成员的利益，必须对供应链进行协调。本文研究在产量随机、需求受价格影响的环境下一个供应商、一个制造商和一个零售商组成的三级供应链中的协调问题。重点分析了供应商在需求和产量不确定情况下如何进行订货批量的决策的问题，还分析了供应商、制造商和零售商的价格策略问题。首先对供应链进行集中决策模型的分析，为分散决策建立一个基准，通过纳什博弈和斯坦伯格博弈对比分析，最终采用夏普里合作博弈使得各个成员的利润都比分散情况下的大，达到一个共赢的局面。

Abstract： Supply chain coordination in supply chain management is an important area of research， in order to achieve the overall supply chain optimization without harm to the interests of all members of the supply chain， the supply chain must be coordinated. In this study， yields random， subject to price. We considered a supplier， a manufacturer and a retailer in the supply chain， and analyze the coordination problems which suppliers in demand and production uncertainty. We mainly talk about how to order quantity decisions， and analyze the problem of pricing strategies. First， we carry on the analysis focused on the supply chain decision model to establish a baseline for decentralized decision-making， and through the Nash game and Steinberg game analysis， make the eventual adoption of Shapley profit cooperative game larger than the dispersion of individual members， reaching a win-win situation.

关键词： 供应链协调；纳什；斯坦伯格博弈；夏普里

Key words： supply chain coordination；Nash；Stackerberg game；Shapley

中图分类号：F274；F224.32 文献标识码：A 文章编号：1006-4311（2017）09-0079-05

1 介绍

经济全球化和生产全球化使供应链成为不可逆转的趋势，企业间的竞争逐渐转化为整个供应链之间的竞争，一条供应链通常有制造商，分销商和零售商等组成，其中有买卖关系，通常他们由不同的实体组成。所以，在做决策时，他们都会从自身利益最大化的角度出发，而忽略供应链的整体利益最大化的目标，由此产生一种双重边际效应，而供应链的信息不对称也会造成一种牛鞭效应，这两种效应都会使供应链的整体效率下降，为了解决双重边际化效应或多重边际化效应对供应链所产生的不良影响，供应链参与各方可以达成一些激励约束机制，以使供应链参与各方的个体理性行为与集理理性行为趋于一致。市场需求和产量的不确定是导致不协调的主要因素。协调最终的目的都是为应对不同情况，运用最多的办法是签订契约机制，对供应链中所有的成员进行有效的激励和约束从而保证这些成员在进行决策时能够做出使集体最优的决策。在供应链契约形式上有各自的特点，最常见和最基本的有批发价格契约、回购契约、收益共享契约、弹性数额契约、普通期权契约等，也可由两种或几种契约配合使供应链达成整体最优，即使无法达到最佳协调状态，也可达到帕累托最优。

2 文献综述

从1960年代开始，很多学术工作就一直专注于不确定环境下的供应链。在以往的很多研究中，都是以确定性需求为前提条件的，如传统的经济订购数量（EOQ）模型就是假设需求确定，基于此模型的很多研究由于太过于理想化，而不具有太多的实际意义，所以很多学者做了关于需求不确定下供应链协调方面的研究。弹性需求、随机需求与模糊需求是不确定需求的几种特殊形式。

刘永胜和李敏强从供应商的角度出发，研究弹性需求情形下基于共同补给期的协调策略问题。核心是要阐明共同补给期协调策略如何能够实现供应链的协调运作。文章提出年需求按是否提供折扣分为两种，都是关于价格的函数。SeyedEsfahani and Biazaran提出价格受广告和促销努力的影响，并总结前人的成果建立了自己的需求函数，力求更加贴近现实生活。Fei and Cheng研究了一个制造商和一个供应商在产量随机和需求随机条件下的一种柔性订货策略。Xiao等研究了一个顾客退货、需求随机的两级供应链，消费者对产品评估也具有不确定性。He and Zhao研究需求和供应随机环境下多级供应链的库存、生产、合同的制定。桑圣举为保证供应链成员获得利润，在模糊需求环境下，研究由单一供应商和零售商组成的两级供应链系统的协调机制问题。将市场需求视为模糊变量，建立不确定理论下基于可信性分布的分散决策、集中决策，以及收益共享契约和回购契约模型并以三角模糊变量为例对模型进行优化，给出各种模型下的最优策略。白世贞和徐娜针对一个由供应商-制造商-零售商构成的三层供应链，在考虑市场需求为模糊变量的情况下，通过不确定理论分别建立了基于可信度分布的集成供应链模型和收益共享契约模型，并求出最优策略，結果表明，零售商以及制造商的最优订购量在模糊需求中心点的左右浮动。Zhao and Wei将供应链的需求作为模糊变量，需求受价格和销售努力的影响。管理者根据判断、经验、才智等对不确定的参数进行大约的估计。

博弈论的使用在供应链决策中有重要作用。大多文献通过Stackelberg博弈来分析制造商和零售商处于不同的谈判地位时的动态定价决策等问题。Fei and Cheng，宋华明和杨慧，徐广业和但斌，葛静燕和黄培清等使用Stackelberg博弈模型来分析单一制造商和单一零售商组成的供应链，当制造商和零售商采用分散决策时，制造商是价格的制定者，零售商是价格的追随者。李绩才和周永务等在非一体化决策时，供应商和零售商均从各自的角度采取优化决策。考虑供应商与n个零售商之间的Stackelberg主从对策问题，零售商彼此间是纳什博弈问题。包裕玲考虑单个供应商，多个不同成本结构的订货商供应链协调系统。等建立了制造商为主方、零售商为从方的供需Stackelberg博弈模型。Stackelberg博弈和其他博弈模型比较，肖剑等在对称信息的框架下，建立了双渠道供应链中制造商电子渠道与零售商服务合作的Stackelberg and Bertrand博弈模型。SeyedEsfahani and Biazaran从纳什博弈、斯坦伯格-制造商博弈、斯坦伯格-零售商博弈和合作博弈四个角度研究了供应链纵向合作广告问题。He and Zhao研究多级供应链的库存、生产、合同的制定。建立了分散决策情况下以制造商为主，零售商跟从的博弈模型，并结合合作博弈模型，纳什讨价还价的分析。

契约机制是一种实现供应链协调有效的方法，传统契约有退货政策或回购契约、收益共享契约、批发价格契约、风险共担契约、数量折扣契约、数量柔性契约、销售折扣契约。其中退货和收益共享是最经常研究的两种契约。近来，许多研究进一步拓展了传统契约，在不同情况下来实现供应链协调。

Tsay提出了供应链契约的两个非常重要目标：第一个是在保证成员企业受益不降低的情况下，提高供应链整體收益以达到集中控制情况下的效果；第二个是风险的共担，即可以通过契约的设计使得供应链成员企业可以共同承担整条供应链的风险，这可以促使各成员企业做出有益于供应链整体和自身的决策。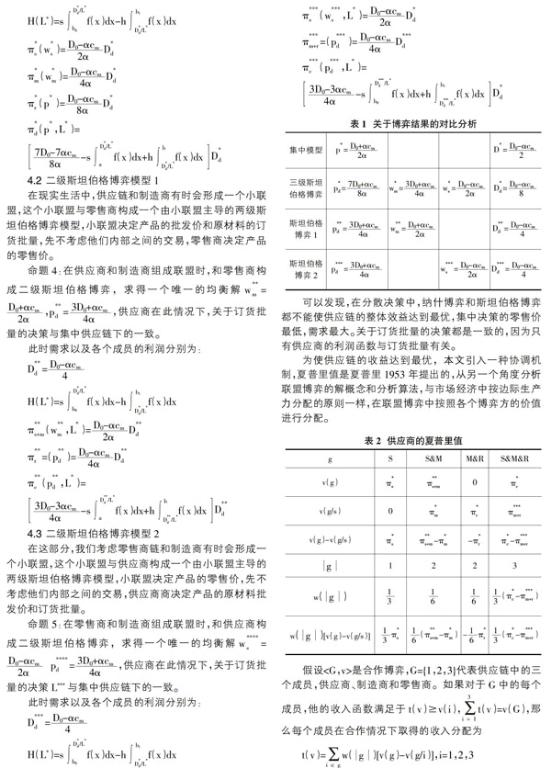

He and Zhao研究发现一般上游和下游供应链成员使用批发价格契约都不能协调供应链系统。然后提出一个制造商和零售商使用的回购契约，结合原材料供应商和制造商使用的批发价格契约可以完美地协调供应链。徐广业和但斌构建了能够实现双渠道供应链协调的收益共享契约模型，给出了实现双渠道供应链协调时，契约参数取值范围的计算公式，并进一步探讨了双渠道供应链完美共赢协调存在的条件。最后通过算例分析，验证了所设计的收益共享契约模型对双渠道供应链协调的有效性。李绩才和周永务等以一个两阶段的供应链系统为研究背景，建立了下游损失厌恶型零售商之间存在竞争的收益共享契约协调模型。葛静燕和黄培清设计了一个RAESC模型（销售收入及回收费用共享契约）改进了Stackelberg均衡的结果，协调了该闭环供应链系统成员的定价策略。简惠云和王国顺[17]设计了价格折扣与回购联合的协调契约，并得到了协调契约下折扣价和销售季末回购价应满足的条件。研究表明，在以制造商占主导地位的二级供应链中实行价格契约，只要批发价存在折扣，零售商采用两阶段订购模式总是能增加其期望利润，但单纯的价格折扣契约不能协调供应链。宋华明和杨慧针对Stackelberg博弈中出现的双重边际效应，结合回购与风险分担两种策略，提出了一种两参数契约，提出了实现供应链协调的契约形式，并论证了实现供应链协调的条件。

Fei and Cheng采用柔性订购政策并提出采用一个新的OPR契约，即收益共享和一种补偿机制相结合。Ding and Chen研究如何在提交最终契约价格决定时通过制定价格标准，用一个柔性退货政策来完全协调一个三级供应链。He and Zhang等研究当下游零售商同时面对努力和价格都基于随机需求时的供应链契约和协调。在这种情况下，由于所有传统契约没能协调零售商的行为，所以他们探索了其他各种各样的联合契约，并且发现只有一个合理的有计划的基于价格折扣和惩罚契约的退货政策才能实现渠道协调，使供应链中的成员实现双赢的局面。Wu考虑了一个基于贝叶斯更新的数量柔性契约的分散控制系统，即零售商给制造商一个初始预测，然后厂家根据零售商的预测安排生产。Granot and Yin[调查了在价格依赖的报童模型中协议顺序的影响，供应商和零售商按顺序提交价格和数量。Rhee等提出一个新的跨越收益共享契约机制，最下游实体发起一个涉及多级供应链中所有上游实体的契约，并分析了在具有随机需求的线性供应链中的新收益共享契约。Tsao研究了一个多阶层多通道供应链，这种供应链取决于供应商的信用度和零售商的促销努力。他们分析了两个贸易补贴，促销成本分担和现金折扣，这是为协调供应链中的合作伙伴的行为而设计的。

在目前的研究中，大多关于供应链协调的研究成果是基于简单的链状结构的供应链系统，而对于复杂的网状系统协调问题研究较少，因此，对复杂的网络状供应链系统协调的研究将会是以后一个重要的研究方向。

3 符号、假设和集中模型

本文考虑的是一个三级供应链，包括一个原材料供应商，一个制造商和一个零售商。首先供应商对原材料粗加工后以一定的批发价出售给制造商，制造商接收到原材料后精加工后以一定的批发价给零售商，零售商最终将产品出售给顾客。

3.1 参数

cs供应商生产原材料的成本

cm制造商对原材料进行精加工的成本

s供应商从现货市场补货的成本

h供应商的库存持有成本

Do市场的基础需求

3.4 分散模型

为了克服信息扭曲和牛鞭效应，许多企业采用了供应商管理库存。由于利益和激励机制的冲突：一方面，销售商为了提高服务水平，希望供应商在仓库中多存货；另一方面，由于库存剩余的风险，供应商不愿在仓库中多存货，供应商管理序存环境下，双边际效应同样存在。本文为了减少这种双重边际效应，本文采用供应商管理库存，库存成本和缺货成本由供应链所有成员共同承担，为了鼓励供应商建立仓库管理库存，并进行批量生产，将产品批售给制造商，供应商粗加工费用也由供应链所有成员共同承担。

5 结论

在以往关于供应链的研究中大多采用二级供应链的模型本文针对产量随机、需求受价格和广告营销影响的环境下一个供应商、一个制造商和一个零售商组成的三级供应链中的协调问题，首先建立决策模型，为供应链整体效率以及关于售价和订货批量的决策建立一个标准，然后讨論分散决策下的博弈模型，分别供应链中所有成员都是平等的情况，三个成员力量不均的情况以及三个成员有小联盟的情况分别就行决策分析，最终通过将五种情况下的决策以及所产生的需求进行对比分析，发现在合作的时候供应链的效率达到最大，由此我们引入夏普里值，供应链所有成员合作，然后按照各个博弈方在联盟博弈中的贡献和价值进行公平分配。夏普里协调机制不仅使整个供应链的效益达到最大，而且相对于分散博弈，提高了每个成员的收益，使整个供应链达到一个共赢的局面，有很重要的实际意义。

这篇论文的创新点主要在于考虑的是产量和需求不确定下一个多级的供应链，在不确定的需求上除了考虑到需求受价格的影响，还考虑到收到营销广告的影响，并且分全国广告以及地方广告，影响程度根据取得系数来表示影响程度的不同。在本篇文章中还考虑到了库存持有成本，供应商在产量不确定的时候产生的不足从第二市场中补货，多了则会形成库存。

文章以后研究的方向：①在广告费的摊销上。②引入一个订货量的决策变量。③受价格和营销影响的需求函数有待商讨。④利用Matlab加入算例分析。

参考文献：

[1]Hu F， Lim C C， Lu Z. Coordination of supply chains with a flexible ordering policy under yield and demand uncertainty[J]. International Journal of Production Economics， 2013， 146（2）： 686-693.

[2]徐广业，但斌，肖剑.基于改进收益共享契约的双渠道供应链协调研究[J].中国管理科学，2010，18（6）：59-64.

[3]李绩才，周永务，肖旦，钟远光.考虑损失厌恶一对多型供应链的收益共享契约[J].管理科学学报，2013，16（2）：71-81.

[4]葛静燕，黄培清，王子萍.基于博弈论的闭环供应链协调问题[J].系统管理学报，2008，16（5）：549-552.

[5]包裕玲.多个订货商的两层供应链 Stackelberg协调博弈分析[J].中国管理科学，2008，16（3）：68-72.

[6]简惠云，王国顺，许民利.具有两阶段生产模式和需求信息更新的供应链契约研究[J].中国管理科学，2013（1）：80-89.

[7]He Y， Zhao X. Coordination in multi-echelon supply chain under supply and demand uncertainty[J]. International Journal of Production Economics， 2012， 139（1）： 106-115.

[8]宋华明，杨慧，罗建强，等.需求预测更新情形下的供应链 Stackelberg博弈与协调研究[J].中国管理科学，2010，18（4）：86-92.

[9]肖剑，但斌，张旭梅.双渠道供应链中制造商与零售商的服务合作定价策略[J].系统工程理论与实践，2010（012）：2203-2211.

[10]SeyedEsfahani M M， Biazaran M， Gharakhani M. A game theoretic approach to coordinate pricing and vertical co-op advertising in manufacturer-retailer supply chains[J]. European Journal of Operational Research， 2011， 211（2）： 263-273.

[11]Zhao J， Wei J. The coordinating contracts for a fuzzy supply chain with effort and price dependent demand[J]. Applied Mathematical Modelling， 2013.

[12]A. Nagurney， F. Toyasaki， Supply chain super networks and environmental criteria， Transport[J]. Res. Part D： Transp. Environ， 2003， 8（3）：185-213.

[13]Q.H. Zhu， Y.J. Dou， An evolutionary model between governments and core-enterprises in green supply chains， Syst[J]. Eng. -Theory Pract， 85 （12） （2007）85-89 （in Chinese）.

[14]M. Serrato， S.M. Ryan， J. Gaytan， Characterization of reverse logistics networks for outsourcing decisions. Iowa State University， 2004.

[15]J.B. Sheu， Y.H. Chou， C.C. Hu， An integrated logistics operational model for green-supply chain management， Transport. Res. Part E-Logist. Transport.Rev. 41 （4） （2005） 287-313.

[16]R.C. Savaskan， S. Bhattacharya， V.L.N. Wassenhove， Closed-loop supply chain models with product remanufacturing， Manage. Sci. 50 （2） （2004）：239-252.

[17]S. Ray， T. Boyaci， N. Aras， Optimal prices and trade-in rebates for durable， remanufacturable products， Manufact. Serv. Oper. Manage. 7 （3） （2005） 208-228.

[18]Y.Y. Yi， Closed-loop supply chain game models with product remanufacturing in a duopoly retailer channel， J. Manage. Sci. China 12 （6） （2009） 45-54（in Chinese）.

[19]G. Easwaran， H. Uster， A closed-loop supply chain network design problem with integrated forward and reverse channel decisions， IIE Trans. 42 （11）（2010） 779-792.

[20]J.M. Shi， G.Q. Zhang， J.C. Sha， Optimal production planning for a multi-product closed loop system with uncertain demand and return， Comput. Oper.Res. 38 （3） （2011） 641-650.

[21]L.S. Shapley， A value for n-persons games， Ann. Math. Stud. 28 （1953） 307-318.

[22]J.C. Harsanyi， R. Selten， A generalized Nash bargaining solution for two-person bargaining games with incomplete information， Manage. Sci. 18 （5）（1972） 80-106.C.-T. Zhang， L.-P. Liu / Applied Mathematical Modelling 37 （2013） 3369-3379-3379