基于马尔可夫方法的违约传染平均域模型

刘久彪

摘 要 基于平均域模型，将信用组合分为几个同质的子组合，假设组合中各公司的违约强度不仅取决于宏观经济状况，而且依赖于这些子组合中违约公司的数目，以刻画不同公司间的违约相互作用;并据此建模组合违约过程为连续时间马尔可夫链，借助Kolmogorov微分方程求解信用组合损失分布;最后，通过实例计算分析传染现象对组合损失分布、风险量度的影响.

关键词 金融管理学;信用组合;马尔可夫方法;违约传染;平均域模型

中图分类号 F830文献标识码 A

Abstract The credit portfolio was divided into several homogeneous sub-portfolio by mean-field model，and the companys default intensity was assumed to depend on macroeconomic conditions and the number of defaulted companies in the sub-portfolio in order to characterize the interaction among different companies.Then，the portfolio default process was modeled as a continuous-time Markov chain，and credit portfolio loss distribution was solved by Kolmogorov differential equation.Finally，we analyzed the influence of default contagion on the portfolio loss distribution and risk measure by the examples.

Key words financial management;credit portfolio;markovian approach;default contagion;mean-field model

1 引 言

自2008年美国次债危机发生以来，全球一直经受着大型金融机构和公司的不良操作所带来的负面影响，也突显出了了解和研究违约相关性及其影响的重要性.违约相关性是指多个金融机构或公司之间违约形势相互影响的关系，目前主要的银行业标准模型（如KMV、CreditMetrics等）都将其归结为不同公司的信用状况均受共同的宏观经济因素（如GDP增长率、股票指数）影响[1];但J.Driessen（2005）、J.Hatchett（2006）和A.Herbertsson（2011）研究显示，和历史数据相比，此类模型产生的违约相关性水平偏低，且无法解释“一些公司易于集中在某段时间内发生违约”的经验事实[2-4].

K.Giesecke（2004）、H.Helen（2007）研究显示，违约相关还存在另一种表现形式，当多个公司间存在关联关系（如商业上直接联系的借贷关系、贸易伙伴;信息效应的间接影响等）时，少数公司的信用危机会以传染的形式蔓延到它的关联公司，造成其违约概率增加，甚至发生违约，称之为违约传染[5-6].K.Giesecke（2006）指出，一個理想的信用组合风险模型应既能体现不同公司受共同的宏观经济因素影响造成的周期性违约相关，又能捕捉关联公司间的违约传染，从而产生符合实际大小的违约相关性[7].

基于平均域模型，将信用组合分为几个同质的子组合，假设各公司的违约强度不仅取决于宏观经济状况，且依赖于这些子组合中违约公司的数目，以刻画不同公司间的违约相互作用，据此建模组合违约过程为连续时间马尔可夫链，借助Kolmogorov微分方程求解信用组合损失分布，并通过实例计算分析传染现象对组合损失分布、风险量度的影响.

2 平均域违约传染模型建立

平均域模型原用于描述大量微观粒子系统中每个粒子与其它粒子以相同方式的相互作用，HFlmer（1994）创造性的将其应用于刻画多个“同质”公司的相互影响，尽管这种“同质”假设十分严格，但仍对大型违约传染组合损失建模具有十分重要的借鉴意义，如果所研究信用组合中各公司具有相同的信用等级、或者属于同一行业（如：能源行业等），那么可认为其产生现金流、增加资产的能力是“同质”的[8].

3 违约传染模型求解的马尔可夫方法

上面将信用组合划分为几个“同质”子组合，并假设组合内各公司违约强度为宏观经济状态和组合中违约公司所占比例的函数，即平均域违约传染模型.下面将证明违约强度满足上面假设的信用组合，在宏观经济过程确定条件下，各子组合违约公司数目分布的向量过程为非时齐次马尔可夫链，并推导组合损失的概率分布函数.

4 实例研究

上面针对资产数目较多、关联关系较复杂的信用组合，建立了平均域违约传染模型，使违约状态转移概率Kolmogorov微分方程对此类组合依然能够保持计算的易于处理性.下面将应用平均域违约传染模型对实例进行具体求解，并分析违约传染现象对信用组合损失分布、尤其是一致性风险量度的影响.

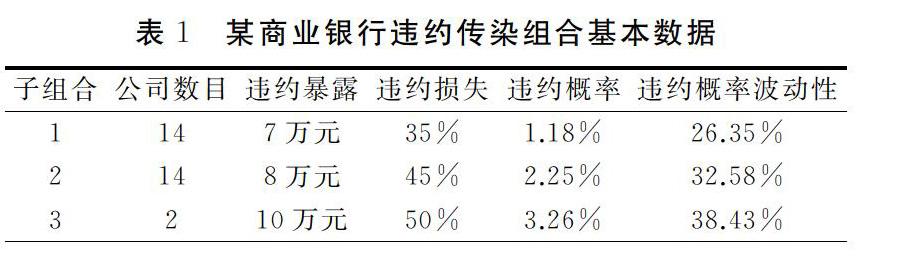
实例：某商业银行一个由30笔中小企业贷款组成的信用组合，其债务人分属3个信用等级，据此将该组合划分为子组合1、2、3，假设各子组合均为“同质”组合.考察各债务公司的资产负债表，发现其在财务、经营方面存在联系，因而存在潜在的相互违约传染，整理组合基本信用数据列表如表1.

在计算过程中发现，对于由30笔贷款组成的信用组合，若直接考虑每两个公司间的相互作用，则组合违约状态空间维度为230，其对应的状态转移概率Kolmogorov微分方程几乎是不可能求解的;而借助相同等级资产的“同质”假设，将组合划分为几个子组合，基于平均域模型建模各子组合公司违约强度为整个组合违约公司比例的函数，则组合违约状态空间的维度减小为15×15×3=675，保证了Kolmogorov微分方程的易于处理性，可利用其方便的求出其各违约状态的发生概率，并进而求出组合风险的VaR和一致性量度ES.

从表2可发现，考虑违约传染现象得出了更大的组合风险量度VaR和ES，而不考虑违约传染现象则会显著地低估风险.这是因为，传染现象会对生存公司的违约强度产生一个正的反馈影响，并由此增大宏观经济因素随机波动引起的组合违约公司数目的波动性，使信用组合损失的尾部分布变“厚”，进而增加其联合违约概率、组合风险量度VaR和ES，这可从图1、2中清楚看出.

从图1可见，相比于不考虑违约传染，考虑传染得出的信用组合损失分布两端变厚，即组合极端大损失和小损失的概率都明显增加.这是因为：当信用组合中出现新的违约、即组合违约比例增加时，违约传染现象对未违约公司的违约强度产生一个正的反馈影响，使其违约强度发生一个正向跳跃，并由此增大了宏观经济因素随机波动引起的组合违约公司数目的波动性，使传染组合损失的尾部分布变“厚”，即联合违约概率增加.这说明违约传染本质上是一种违约相关，其会“压扁”组合的损失分布，使其组合损失尾部变厚，这一点在组合损失尾部概率密度分布中显示得尤为明显.

图2清楚地显示出，考虑违约传染情况下得出的组合损失频率大于不考虑违约传染情况下得出的结果，说明违约传染使得组合损失分布的“厚尾”现象加剧;也说明当组合资产间存在彼此关联时，不考慮违约传染可能会低估风险，特别是应用一致性风险量度ES度量组合风险时.

需要说明，由于平均域违约传染模型按公司信用等级或所属行业将整个组合划分为几个子组合，并假设同属一个子组合各公司具有相同的信用特征，若子组合中存在少数资产违约暴露较大、支配其余多数资产的情况，则需要将这些资产剔出并单独组成子组合;否则，子组合的异质性将造成对信用组合尾部风险的低估，得出的组合VaR、ES会小于实际值.

5 结 论

从以上分析和实例计算，可以得出如下结论

（1）在简化模型下，综合考虑周期性违约和传染违约两种相关结构，建立信用组合中各公司违约强度相互作用的违约传染模型，可以通过求解Kolmogorov微分方程得到精度较高的信用组合损失分布;

（2）借助平均域模型，将信用组合划分为几个“同质”子组合，考虑各子组合之间的相互作用大大减小了组合违约状态空间的维度，保证了Kolmogorov微分方程对于资产数目较大的组合也能求解;

（3）当组合中资产存在违约传染现象时，新的违约会通过传染形式对未违约公司的违约强度产生一个正的反馈影响，使其违约强度发生一个正向跳跃，由此增大了宏观经济因素随机波动引起的组合违约公司数目的波动性，使传染组合损失的尾部分布变“厚”，并进而增加其联合违约概率、组合风险VaR和ES.

参考文献

[1] G.Szeg.Risk Measures for the 21st Century[M].New York：John Wiley & Sons，2004.

[2] J.Driessen.Is Default Event Risk Pricing in Corporate Bonds？[J].Review of Financial Studies，2005（1）： 165-195.

[3] J.Hatchett and R.Kühn.Effects of Economic Interactions on Credit Risk[J].Journal of Physics A： Mathematical and General，2006（9）： 2231-2251.

[4] A.Herbertsson and H.Rootzén.Modelling Default Contagion Using Multivariate Phase-Type Distribution[J].Review of Derivatives Research，2011，14（1）： 1-36.

[5] Giesecke K.Correlated default with incomplete information[J].Journal of Banking & Finance，2004，28（7）：1521-1545.

[6] H.Helen.Modelling Basket Credit Default Swaps with Default Contagion[J].Journal of Credit Risk，2007（1）： 1-25.

[7] K.Giesecke and S.Weber.Credit Contagion and Aggregate Losses[J].Journal of Economic Dynamics & Contral，2006（30）： 741-767.

[8] R.Frey and J.Backhaus.Portfolio Credit Risk Models with Interacting Default Intensities： A Markovian Approach[J].University of Leipzig，Working Paper，2004.

[9] Fan Yu.Correlated Defaults in Intensity-Based Models[J].Mathematical Finance，2007，17（2）：155-173.

[10] Lux T.A model of the topology of the bank – firm credit network and its role as channel of contagion[J].Journal of Economic Dynamics & Control，2016（66）：36-53.

[11] Batiz-Zuk E，Christodoulakis G，Poon S H.Credit contagion in the presence of non-normal shocks[J].International Review of Financial Analysis，2015（37）：129-139.

[12] Fink K，Krüger U，Meller B，et al.The credit quality channel： Modeling contagion in the interbank market [J].Journal of Financial Stability，2016（25）：83-97.