Grid-Search和PSO优化的SVM在Shibor回归预测中的应用研究

张剑 王波

摘 要 作为一种动态和非稳定时间序列，Shibor发展变化是随机波动的，难以准确预测Shibor的波动性.支持向量机（SVM）在回归预测非线性时间序列方面有很好地预测效果，SVM的预测精度和泛化能力的核心是参数的优化选择，分别用网格搜索法（Grid-Search）和粒子群（PSO）算法来优化SVM的参数c和g.从而将参数优化后的SVM非线性回归预测法与基于传统ARIMA时间序列预测结果进行对比分析.实验表明，优化后的SVM回归预测方法比ARIMA时间序列方法更精确，在实际中具有很大的应用价值.

关键词 机器学習;非线性回归预测;支持向量机;网格搜索法;粒子群算法;Shibor

中图分类号 F830文献标识码 A

Abstract As a dynamic and unsteady time series，the development of Shibor is a random fluctuation，and it is difficult to accurately predict the volatility of Shibor.Support vector machine （SVM） has a good predictive effect in the regression prediction of nonlinear time series.SVMs prediction accuracy and generalization ability are due to the optimization of parameters.Grid-search and Particle Group （PSO） algorithm were used to optimize SVM parameters cand g.The SVM nonlinear regression prediction method with parametric optimization was compared with the traditional ARIMA time series prediction results.The experiments show that SVM regression prediction method is more accurate than ARIMA time series method，and it has great application value in practice.

Key words machine learning;nonlinear regression prediction;support vector machines;grid-search algorithm;particle swarm optimization;Shibor

1 引 言

随着近年来我国利率市场化进程的不断加快，作为我国宏观调控政策工具的利率，其使用的频率也越来越高.上海银行间同业拆放利率（Shibor）能够及时、准确地反映出货币市场资金的供求关系，在货币市场中有着举足轻重的地位.其变动会迅速影响和传导我国金融市场，从而影响银行和投资者的投资决策，准确预测预测Shibor的变化趋势以防范利率风险显得尤为重要.因此，Shibor的预测研究对金融风险控制和金融资产定价都具有非常重要的理论和实践意义[1].

国内的许多学者也对Shibor的走势进行了研究.任兆璋和彭化非（2005）构造了我国Shibor利率期限结构，建立了条件异方差自回归GARCH以及自回归移动平均ARIMA模型，实证分析得出ARIMA模型在隔夜Shibor利率走势预测中效果较好[2].田敏等（2009）基于ARMA模型对Shibor进行实证分析，预测结果表明短期的Shibor预测误差较小，预测效果较好，但随着时间跨度的增大，模型预测的精度越来越小，预测的误差也越来越大[3].林宇等（2016）引入了隐马尔科夫模型，基于HMM-CARCH来预测隔夜的Shibor数据，实证结果发现HMM（2）-EGARCH模型的预测能力较好[4].以上这些学者都是基于传统的ARIMA模型和ARCH/GARCH类模型以及这些模型的扩展模型等金融时间序列的分析方法.这些模型虽然短期预测效果较好，但还存在着一定的不足和局限性.随着近些年来支持向量机（SVM）和人工神经网络（ANN）等机器学习方法的快速发展与应用，其也被逐渐运用于金融时间序列数据的分析处理与预测中.谢小璐等（2012）是将小波神经网络应用于Shibor变化趋势的预测中，预测结果表明基于小波神经网络构建的Shibor预测模型比传统时间序列模型的预测效果要好[5].林庆添（2016）从人工智能的角度来预测Shibor的走势，分别使用了BP神经网络、小波神经网络和布谷鸟搜索优化的小波神经网络对隔夜Shibor进行预测分析，结果表明优化后的小波神经网络拟合的效果更好[6].在前人研究成果的基础上，提出一种基于SVM的回归预测方法，并利用Grid-Search和PSO算法来优化SVM的参数c和g找到全局最优解，以提高预测精度.

2 支持向量机统计学习理论

统计学习理论所研究的是有限样本或者小样本条件下的统计估计和预测学习理论.SVM是基于统计学习的结构风险最小和VC维理论之上的机器学习方法，因其具有完善的理论基础，良好的分类和预测性能而得到了学者们的广泛研究与应用.[7-8]

2.1 线性支持向量机

最优的回归超平面则是全部根据落在两条边界线上的样本点来确定，此时的样本点就是支持向量.所要寻找的最优回归超平面就是使得几何间隔最大的分离超平面，线性可分SVM最优的学习策略可表示为：

其中‖w‖是向量w的第二范数.此时目标函数是二次函数且约束函数是仿射函数，上式凸最优化学习策略问题就变为了求解凸二次规划问题.为了求解得到线性可分支持向量机的最优解，应用拉格朗日对偶性，通过求解对偶问题得到原始问题的最优解.对偶算法如式（2）所示，这样做的目的是可以更加简单快捷求解原问题，与此同时还可以加入核函数的概念，从而可以运用到非线性支持向量机.

2.2 线性不可分支持向量机

2.3 非线性支持向量机与核函数

3 改进的SVM参数选择方法

参数选择在很大程度上会影响支持向量机回归的准确性，关于SVM参数的优化选择问题，到目前为止，学术界还没有公认统一的最好方法.现在，比较常用的参数寻优的方法包括：粒子群算法、实验法、遗传算法、网格搜索法等.

3.1 网格搜索法和粒子群算法

网格搜索法的基本原理就是让参数c和g在一定的取值范围内划分网格并遍历网格内所有点.对于取定的c和g利用K-CV方法得到在此组c和g下训练集的准确率，最终取使得训练集准确率最高的那组c和g作为最佳的参数.

粒子群算法也叫鸟群觅食算法，源于复杂适应系统，它是一种启发式算法.其基本的思想就是通过群体中个体之间的相互协作和信息共享，最终达到群体最优目的的行为.在搜索最优参数时，把寻优的c与δ看作粒子群算法中的粒子，从随机解出发，不断地进行迭代来求解最优解.它简单且易实现，被广泛应用于神经网络的优化、参数寻优、控制系统及其他领域.

3.2 Grid-Search和PSO优化SVM的方法

网格搜索方法在参数寻优的过程中，只要是在所取的区间足够大并且步距足够小的情况下，就可以搜索到全局最优解.但这种方法由于惩罚系数c值过大，容易导致过拟合，模型的泛化能力不好，而且遍历网格将会浪费大量的时间.通过对SVM非线性回归预测原理的分析，我们可以看出参数c与g的选择好坏将很大程度上决定Shibor预测的准确度.

基于以上分析，如果可以先确定一个比较好的参数寻优区间，接着进行精确地搜索，就能够大大精简计算，提高运算效率和精度.一种改进的SVM参数寻优的方法是利用Grid-Search和PSO算法来优化SVM参数.先利用网格搜索法大范围大步距地粗略搜索，初步确定一个最优参数范围，接着利用PSO进行小步距小范围地精确搜索，进行二次参数寻优，避免了粒子群算法容易陷入局部最优的问题.

4 Shibor回归预测模型的建立

4.1 样本数据的获取及预处理

Shibor数据利用python获取，语法为shibor=ts.shibor_data（2016）.选取的是2016年8月10号到2017年2月17号，取前100个数据作为训练集，后30个数据作为预测集.为了提高算法的预测准确率和收敛速度，对原始的Shibor数据进行归一化处理，采用归一化映射将数据归一化到[0，1]之间，归一化公式如下所示.

4.2模型的建立

4.3训练结果与分析

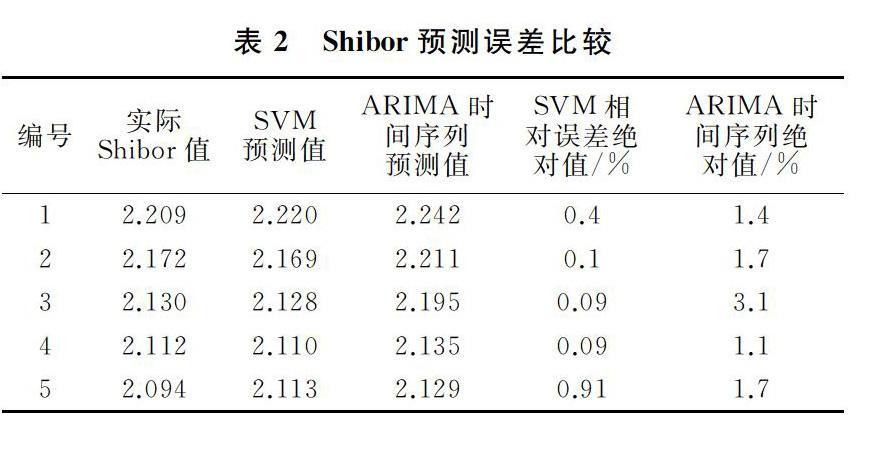
4.4 与ARIMA时间序列预测的对比分析

5 结 论

首先阐述了准确预测作为我国货币市场核心利率的Shibor的重要性，分析了用于回归预测的支持向量回归机的理论基础，运用LIBSVM建立了基于Grid-Search和PSO算法优化的SVM模型，提高了预测的效率和准确率.接着选取了2016年8月10日到2017年2月16日的Shibor数据作为训练数据和测试数据.最终将参数优化后的模型得到的预测结果与传统的金融时间序列预测结果进行对比分析.实验结果表明，优化后的SVM非线性回归预测比传统时间序列预测效果要好，在金融研究中具有很好的应用价值.

参考文献

[1] Naimzada A，Pireddu M.Real and financial interacting markets： A behavioral macro-model[J].Chaos Solitons & Fractals，2015，77（1）：111-131.

[2] 彭化非，任兆璋.中国银行间同业拆借利率预测模型研究[J].南方金融，2005（1）：23-25.

[3] 田敏，李純青，马雷.基于时间序列的上海银行间同业拆放利率（Shibor）[J].宁夏大学学报（人文社会科学版），2009，31（2）：129-132.

[4] 林宇，陈粘，陈宴祥.基于HMM-EGARCH的银行间同业拆放利率市场波动预测研究[J].系统工程理论与实践，2016，36（3）：593-603.

[5] 谢小璐.基于小波神经网络的Shibor预测研究[J].金融理论与实践，2012（8）：57-60.

[6] 林庆添.基于人工智能算法的上海银行间同业拆放利率预测[D].兰州大学，应用统计，2016.

[7] 张学工.关于统计学习理论与支持向量机[J].自动化学报，2000（01）：36-46.

[8] 李航.统计学习方法[M].清华大学出版社，2012.

[9] 曾鸣，林磊，程文明.基于LIBSVM和时间序列的区域货运量预测研究[J].计算机工程与应用，2013（21）：6-10.

[10] 颜晓娟，龚仁喜，张千锋.优化遗传算法寻优的SVM在短期风速预测中的应用[J].电力系统保护与控制，2016（09）：38-42.