巷道顶板三维板梁结构的传力机制研究*

周　波，袁　亮，薛俊华，薛　生

(1. 安徽理工大学 能源与安全学院， 安徽 淮南 232001；2. 淮南职业技术学院 能源工程系， 安徽 淮南 232001；3．深部煤炭开采与环境保护国家重点实验室， 安徽 淮南 232001)

0　引言

巷道围岩结构承载着顶板活动引起的矿山压力，其稳定性影响井工安全、高效、绿色开采的精准进行[1-5]。深部高地应力、采动支承应力、采动动载应力及渗流水化协同作用下，岩石材料、支护体组成的巷道围岩结构将面临承载能力的新挑战，极易出现支护体破断失效、岩体大变形破坏、煤与瓦斯突出、冲击矿压等煤岩动力灾害。掌握围岩结构的承载机理对于维护服务期内巷道的整体稳定性至关重要。

受地心引力、构造运动的影响，未受人为扰动的煤系地层处于由自重应力和构造应力组成的原岩应力场中，呈压实平衡的运动状态，积累了不同量级的弹性变形能，工程开挖后的岩体强度和刚度不足以抵抗原岩应力引起的扰动应力时，工程岩体将发生破坏、失稳，影响安全施工[6]。目前国内外学者均采用原位地质力学测试的方法反演原岩应力的分布状态，取得了广阔的工程应用[7-9]，但以某几个测点反演整个地层的应力场存在系统误差，且无法反映层间结构面及岩体变形对应力场的影响。基于此，建立层状岩层静载应力传递的力学模型，考虑层间结构面和岩层变形对应力场的影响规律，揭示巷道开挖前后，顶板结构内应力场的演化规律，为巷道围岩结构承载机理提供理论基础。

1　层间结构面的弹性承载机理研究

1.1　力学模型

承载后的层间结构面将发生法向位移和切向位移，是一个储能结构。微观力学法和经验公式法被广泛应用于求解结构面的本质力学关系，著名的有线弹性模型、双曲线模型、Goodman双曲线模型、指数函数模型、幂函数模型、动态压缩变形模型、动态双曲线模型、三参数模型等[10]。考虑模型的复杂度和确定模型参数的难易程度，选择线弹性模型来描述煤系地层层间结构面的力学响应，其本质力学关系如图1所示。

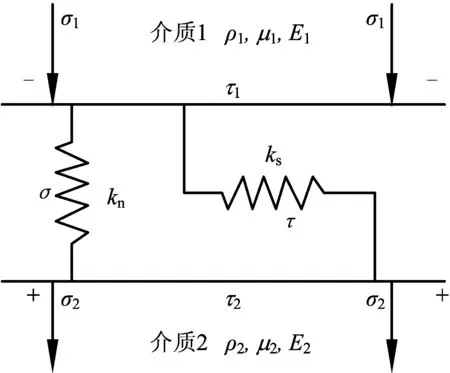
图1　层间结构面内的地应力吸收模型Fig.1　Geostatic stress absorbing model of interlayer structure plane

假定岩层介质1的密度为ρ1，泊松比为μ1，弹性模量为E1；岩层介质2的密度为ρ2，泊松比为μ2，弹性模量为E2。静载应力作用于岩层介质1，经层间结构面传递到岩层介质2，结构面两侧的应力连续，位移不连续，处于静力平衡状态，可建立如式(1)所示的应力平衡方程，求解可获得应力加载条件下层间结构面的位移解，如式(2)，依据功能原理[11]，可求得层间结构面在地层中储存的弹性应变能密度，如式(3)，依据该应变能密度，结合微积分原理，可求得层间结构面任意邻域内储存的应变能大小。

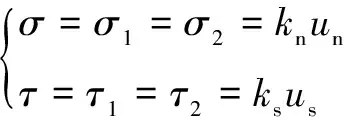
(1)

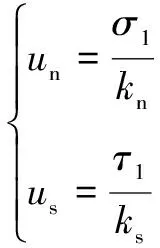
(2)

(3)

式中：σ和τ为岩层的法向应力和切向应力，MPa；σ1和σ2为岩层1和岩层2的法向应力，MPa；τ1和τ2为岩层1和岩层2与层间面之间的切向应力，MPa；kn和ks为综合法向刚度和切向刚度，MPa/m；un和us为层间结构面的位移，m；UP为层间结构面储存的弹性应变能，MJ，其单位面积上的应变能密度为MJ/m2。

1.2　试验分析

完整煤系地层的层间结构面内储存了大量的弹性应变能，掌握此类应变能的储存特征对于研究地下空间工程(如巷道或者工作面等)开挖过程中的能量释放、应力演化、变形破坏、稳定性控制具有深远的指导意义。采用控制变量结合正交试验的方法研究层间结构面的法向刚度、切向刚度、法向应力、切向应力对层间结构面储存弹性应变能密度的交互影响规律。其研究方案见表1，可获得法向应力与其他参数对层间结构面储存弹性应变能密度的作用规律，如图2所示。

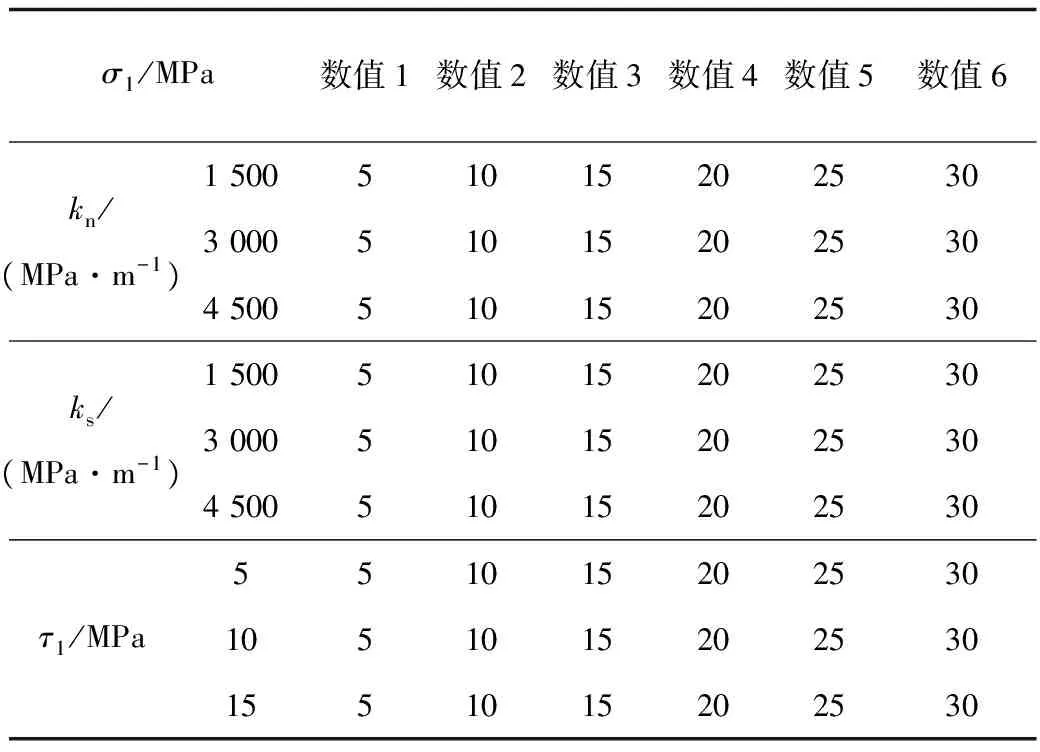
表1　法向应力对层间结构面储存弹性应变能密度的研究方案

由图2可知，层间结构面储存的弹性应变能密度与结构面结构的法向刚度、切向刚度、法向应力、切向应力相关。随着法向应力的增加，应变能密度呈抛物线规律增加的趋势，且随着法向刚度的增加增幅呈显著减小的变化规律，法向应力越大，增幅衰减越明显；随着切向刚度的增加，层间结构面储存的弹性应变能密度随法向应力的增加呈抛物线增加趋势，增幅相差不大，呈整体平移的现象；随着切向应力的增加，呈抛物线增加的结构面结构内弹性应变能密度呈增加的变化规律，增幅变化较小。因此，固有属性法向刚度和切向刚度决定了层间结构面储存弹性应变能的能力，决定了应变能密度随外载荷增加的变化速度，外载荷法向应力和切向应力决定了结构面结构的实际存储弹性应变能大小。

2　岩层变形对应力的扰动作用分析

2.1　计算模型

煤系地层呈现显著的非均质和各向异性的分布形态，各岩层承载后的力学行为存在差异。基于组合梁理论，建立采场覆岩载荷计算模型，可获得岩层载荷计算方法，如式(4)[12]。式(4)反映了第1层岩层所控制的a层岩层对第1层岩层的作用应力，基于应力通过岩层逐层传递这一属性，将第b+1层至第a层岩层的作用应力简化为作用到b层的均布力，该模型被简化为第1层岩层控制上方b层岩层的运动(图3)，据此可求解出a层岩层当中任意岩层上的作用应力，如式(5)。

(4)

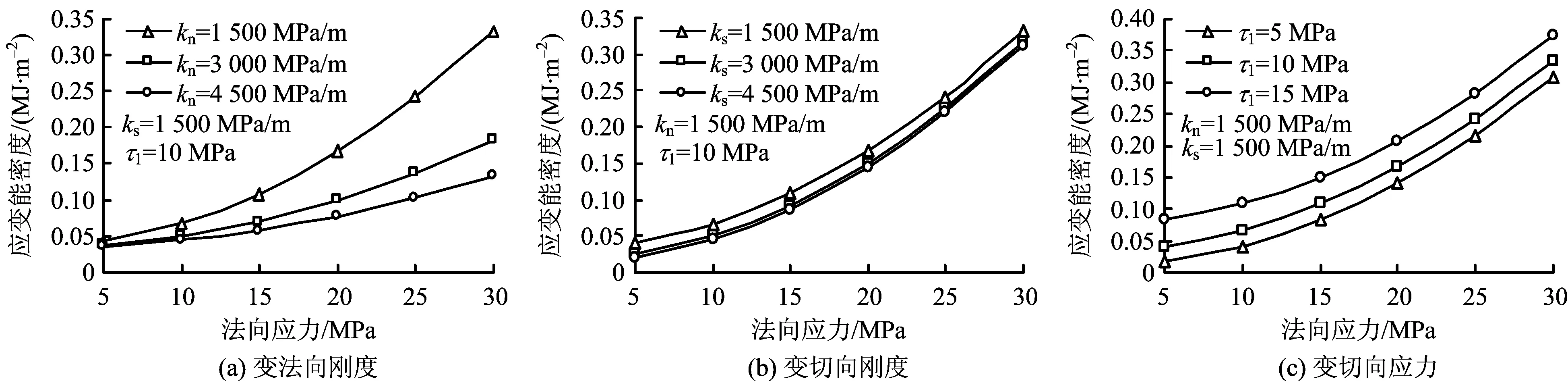
图2　层间结构面的储能规律Fig.2　The law of energy storage of interlayer structure plane

图3　沉积地层静载应力传递模型Fig.3　Transfer model of dead load stress of sedimentary formation

(5)

式中：(σa)1是上方a-1层岩层对第1层岩层的作用应力，包含第1层岩层的自重，MPa；E1，E2，…，Ea是各岩层的弹性模量，MPa；h1，h2，…，ha是各岩层的厚度，m；γ1，γ2，…，γa是各岩层的体积力，N/m3。

为了分析层状岩层的几何属性、力学属性对静载应力的扰动作用，提出用式(5)计算出的应力值与用覆重计算出的应力比值作为岩层属性对静载应力的扰动分析因子，如式(6)：

(6)

2.2　扰动作用分析

以两层岩层为例，开展岩层2对岩层1的作用应力对比分析，首先假定第1层岩层的容重、厚度、弹性模量为0.02 MN/m3，1.0 m，20 000 MPa，然后变化第2层岩层的容重、厚度、弹性模量，见表2，采用控制变量的方法，研究各参数变化引起的扰动因子的变化规律，详细结果如图4。

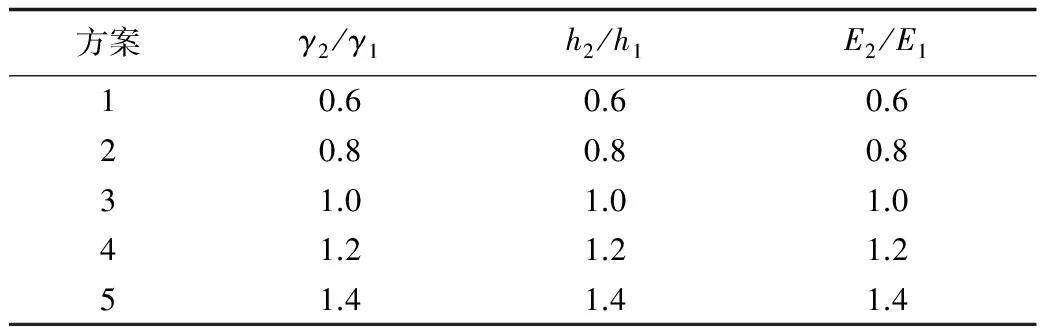
表2　煤层顶板围岩应力计算参数

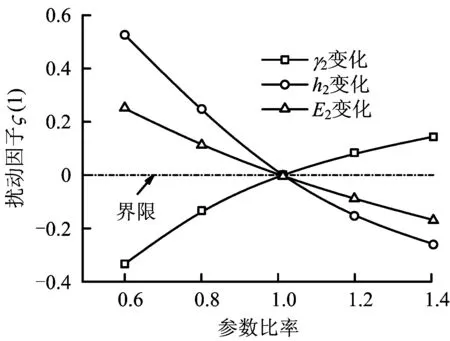
图4　岩性对静载应力的扰动作用Fig.4　Disturbance of lithology acting on dead load stress

由图4可知，当岩层1与岩层2的厚度(1.0 m)、弹性模量(20 000 MPa)相同时，随着岩层2容重的增加，扰动因子呈增幅逐渐减小的增加趋势，且当岩层2的容重小于岩层1的容重时，扰动因子小于0，表明岩层2对岩层1的作用应力为0，岩层2的重量完全由本身承载，当岩层2的容重大于岩层1的容重时，扰动因子大于0，表明岩层2对岩层1的作用应力大于0，且岩层2的容重越大，对岩层1的作用应力越大，但均小于岩层2的自重应力，说明岩层2的重量一部分由岩层1承载，一部分由岩层2本身承载。

当岩层1与岩层2的容重(0.02 MN/m3)、弹性模量(20 000 MPa)相同时，随着岩层2厚度的增加，扰动因子呈减幅逐渐减小的减小趋势，且当岩层2的厚度小于岩层1的厚度时，扰动因子大于0，且厚度越小，扰动因子越大，表明岩层2对岩层1的作用应力大于0，但均小于岩层2的自重应力，说明岩层2的重量一部分由岩层1承担一部分由岩层2自身承担；当岩层2的厚度大于岩层1的厚度时，扰动因子均小于0，表明岩层2对岩层1的作用应力为0，岩层2的重量完全由岩层2自身承担。

当岩层1与岩层2的容重(0.02 MN/m3)、厚度(1.0 m)相同时，随着岩层2弹性模量的增加，扰动因子呈减幅逐渐减小的减小趋势，且当岩层2的弹性模量小于岩层1的弹性模量时，扰动因子大于0，且弹性模量越小，扰动因子越大，表明岩层2对岩层1的作用应力大于0，但均小于岩层2的自重应力，说明岩层2的重量一部分由岩层1承担一部分由岩层2自身承担；当岩层2的弹性模量大于岩层1的弹性模量时，扰动因子均小于0，表明岩层2对岩层1的作用应力为0，岩层2的重量完全由岩层2自身承担。

上部岩层(岩层2)相对于下位岩层(岩层1)的厚度越小、容重越大、弹性模量越小，扰动因子越大、越远离0，上部岩层对下位岩层的作用应力越大，但均小于上部岩层的重量，表明岩层的重量一部分由下位岩层承担，一部分由岩层本身承担处于静载平衡状态。当上部岩层的厚度大于下位岩层厚度、容重小于下位岩层的容重、弹性模量大于下位岩层弹性模量时，扰动因子小于等于零，上部岩层对下位岩层的作用应力为零，即岩层厚度、岩层容重、弹性模量决定了岩层间结构面的相互作用应力大小。该规律可以推广应用到多层岩层的承载传力状态求解。

3　顶板层状岩层弹性承载机理研究

3.1　能量分析模型

岩体变形能产生于外载作用后的岩石材料微观、细观和宏观上的体积、形状的变化过程，将以各类能量的相互转化和物质交换发生能量耗散[13-15]，是一个极其复杂的能量交换系统，可作为由岩石材料组成的岩体结构承载性能的评价分析指标。在弹性变形阶段，储存变形能的大小决定了岩层结构的承载能力，弹性变形能较高预示着岩层结构变形-破坏-失稳需要更强的外载作用，反衬出较强的岩层承载能力。借助能量法来讨论弹性范围内的巷道顶板结构承载特征，对于达到强度极限后的塑性承载不予讨论。

结合式(3)和(5)可求解出第b层层间结构面内储存的弹性应变能密度，如式(7)。依据克拉贝依隆原理[16]，结合第b层岩层的挠度公式(式8)[17]，可求解出第b层岩层内储存的弹性应变能密度，如式(9)。为了形象的描述层间结构面对静载应力的扰动作用，揭示层状岩层结构承载的物相本质，建立层状岩层结构承载特征的能量分析模型，简称能量分析模型，如式(10)。

(7)

(8)

(9)

(10)

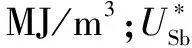
3.2　弹性承载特征分析

能量分析模型认为各岩层的负载为上部岩层的作用应力、岩层的自重应力、

下位岩层的作用应力叠加结

果，由岩层和其下方的层间结构面承担，最大的特点是考虑了弹性层间结构面的承载作用。弹性变形阶段的层间结构面起到了承上启下的传力作用，并具有一定的承载能力，如图5。以极限应变作为岩层的破坏分析指标，结构面对岩层的极限应变没有影响，只要岩层达到极限应变，岩层将进入屈服破坏的塑性承载状态，结构面显著提高了弹性阶段岩层的承载能力，使岩层达到相同的应变所承载的弹性应变能密度显著提高，将图5中的阴影部分定义为结构面对岩层整体承载能力的提高部分。

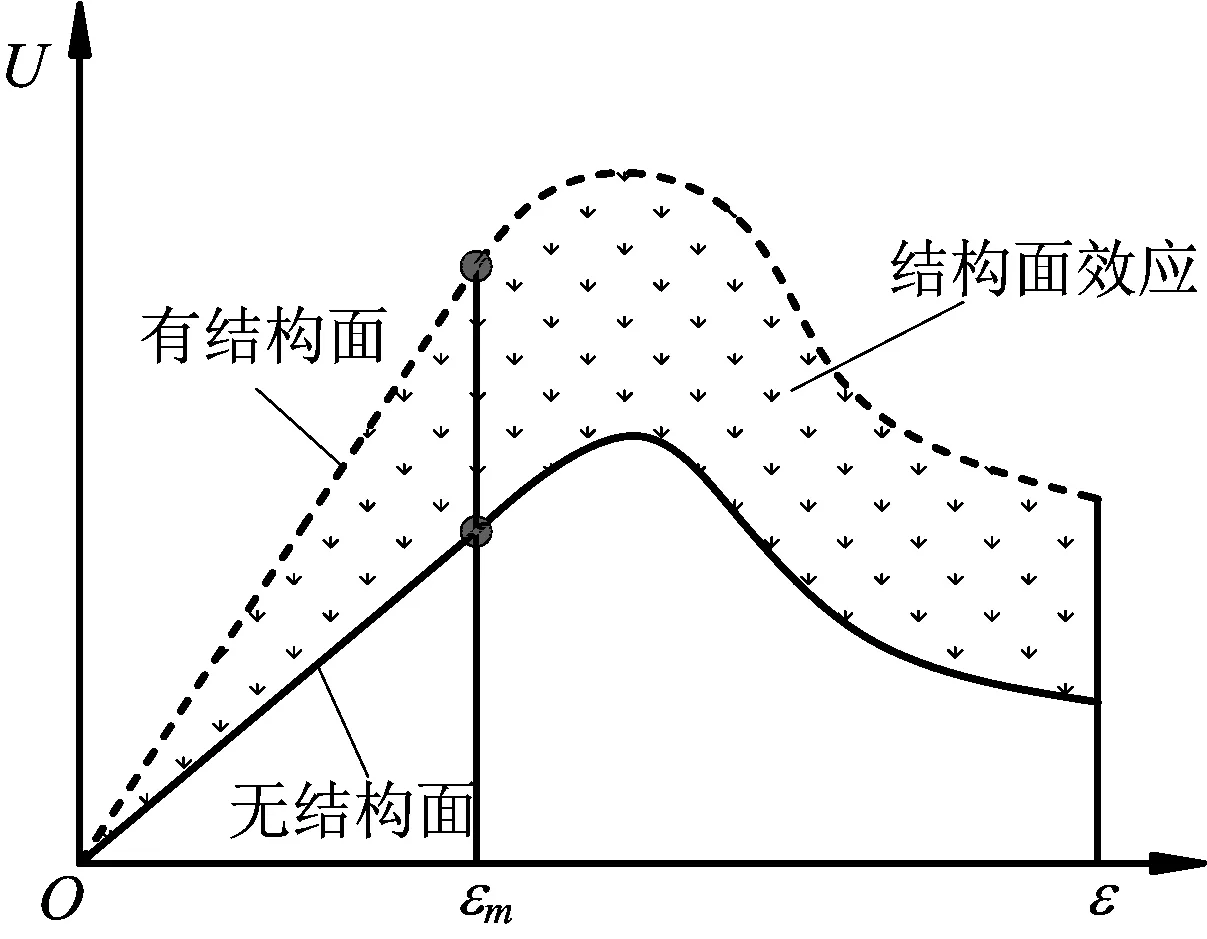
图5　岩层承载能量分析模型Fig.5　Disturbance of lithology acting on dead load stress

4　工程应用

以淮南张集矿1412A工作面为例，开展工程应用。1412A工作面位于西二采区，南侧为西二采区1#煤系统巷道，东侧1413A工作面已回采完毕，西侧为尚未施工的1411A工作面，北至-470 m初设回采上限。工作面平均埋深560 m，走向长1 172 m，倾斜长180 m，属于1#煤层，煤层厚度3.54～8.6 m、平均7.1 m，倾角3～9°、平均5°，顶板45.6 m范围内岩性及岩石力学性质见表3。

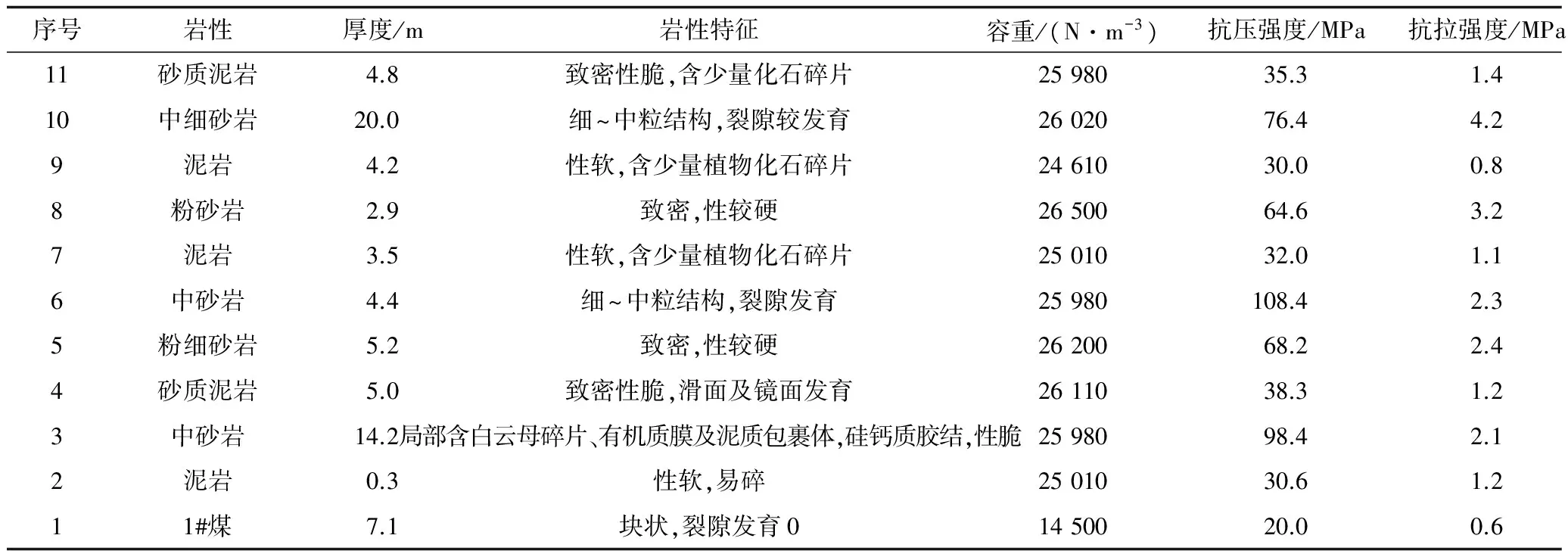
表3　张集矿1412A工作面顶板岩石力学参数

分析表3的数据可知，1#煤开采后，直接顶板为0.3 m厚的软弱泥岩，将随工作面的推进而垮落，无法承载上方岩层的重量，而其上方的基本顶为厚14.2 m厚的中砂岩，较坚硬，可以承载上方岩层及自身重量，将第3层至第11层岩层带入到式(4)可得，第3层岩层至第11层岩层对第3层岩层的作用应力分别为0.37、0.48、0.59、0.68、0.75、0.81、0.90、0.41、0.43 MPa。发现计算到第10层中细砂岩时，第3层岩层承载由0.90 MPa降低到0.41 MPa，所以该类条件下，第3层顶板断裂前，其上方载荷应为0.90 MPa。将第3层岩层的作用应力0.90 MPa，层厚14.2 m，抗拉强度2.1 MPa，代入到固支梁的极限拉断跨距解析式可得该类条件下基本顶初次断裂步距为30.7 m[12]。

(11)

式中:L为固支梁极限拉断跨距，m；h为基本顶层厚，m；RT为基本顶抗拉强度，MPa；q为基本顶所受应力，MPa。

选取初采期工作面下部5#、15#、25#，工作面中部35#、45#、55#、65#、75#和工作面上部85#、95#、105#液压支架的初次来压步距为依据，分析理论计算基本顶初次断裂跨距的真实性，现场观测结果见表4。工作面初次来压步距为23.3～27.6 m(不含切眼的跨度)，判定初次来压平均步距为30.6 m(含切眼跨度5 m)，与理论计算结果30.7 m基本一致，由此可判定，通过理论公式计算的载荷可用于判定基本顶断裂的位置和断裂步距，具有很好的工程应用前景。

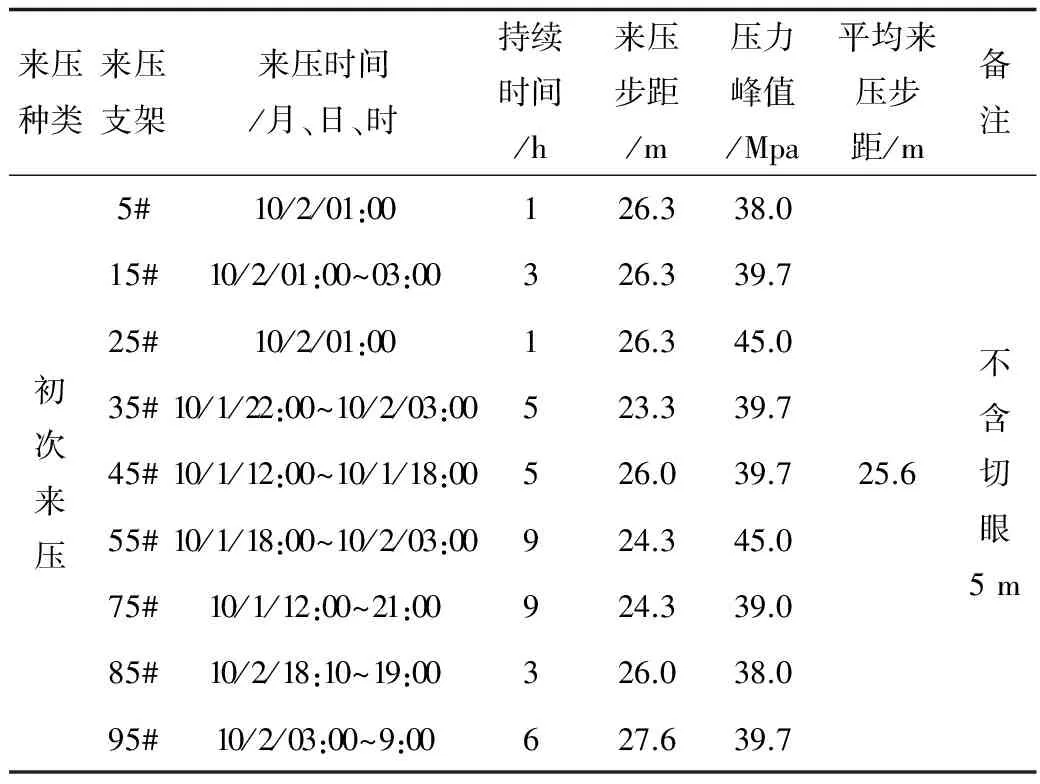
表4　工作面初次来压步距

5　结论

1)层间结构面弹性应变能密度与其法向和切向刚度、法向和切向应力相关，固有属性法向和切向刚度决定了层间结构面储存弹性应变能的能力，决定了应变能密度随外载荷增加的变化速度，外载荷法向和切向应力决定了结构面结构的实际存储弹性应变能大小。相同的方法可以用于分析不同本构模型的结构面内弹性应变能密度变化规律。

2)推导出层状岩体的应力传递解析解(σa)b和扰动分析因子ζb，得到岩层的承载应力是上部岩层的作用应力、自重应力、下位岩层的作用应力叠加的结果。上部岩层的部分自重应力向下经层间结构面传递至下位岩层，传递效率与相邻上下层岩层的容重比呈正相关关系，与层厚比呈负相关关系，与弹性模量比呈负相关关系。

4)计算得到淮南张集矿1412A工作面1#煤开采后，直接顶板软弱泥岩无法承载上方岩层的重量，将随工作面的推进而垮落，1#煤上方第2层岩层的作用应力为0.90 MPa，可得该类条件下基本顶初次断裂步距为30.7 m，与实测初次来压平均步距30.6 m结果基本一致。

[1]韦四江，李奎，吴怡凡，等.冲击地压下巷道围岩失稳机制与控制技术研究综述[J].中国安全科学学报，2016，26(9)：90-95.

WEI Sijiang, LI Kui, WU Yifan, et al. A review of instability mechanism and control technology of roadway surrounding rock under rock burst condition[J].China Safety Science Journal,2016,26(9):90-95.

[2]F Huang ,LH Zhao ,TH Ling , et al. Rock mass collapse mechanism of concealed karst cave beneath deep tunnel [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 91:133-138.

[3]陈梁，茅献彪，李明，等. 基于Drucker-Prager准则的深部巷道破裂围岩弹塑性分析[J].煤炭学报,2017, 42(2): 484-491.

CHEN Liang,MAO Xianbiao,LI Ming,et al. Elastoplastic analysis of cracked surrounding rock in deep roadway based on Drucker-Prager criterion[J]. Journal of China Coal Society,2017,42(2):484-491.

[4]左建平, 孙运江, 李楷，等.陷落柱影响区软岩巷道加固段长度及其底鼓控制研究[J].中国矿业大学学报,2017,46(1): 18-26.

ZUO Jianping, SUN Yunjiang, LI Kai,et al. Study of the reinforced supporting length and floor heave control technology of soft rock roadway influenced by collapse column[J]. Journal of China University of Mining & Technology,2017,46(1): 18-26.

[5]冯友良， 刘栋梁， 罗亚飞.煤巷顶板沉积岩体钻进动力响应特性试验研究[J].中国安全生产科学技术，2016，12(5):31-37.

FENG Youliang,LIU Dongliang, LUO Yafei .Experimental study on dynamic response characteristics in drilling sedimentary rocks of coal roadway roof[J]. Journal of Safety Science and Technology,2016,12(5):31-37.

[6]杨旭旭，靖洪文，陈坤福，等.深部原岩应力对巷道围岩破裂范围的影响规律研究[J].采矿与安全工程学报， 2013，30(4): 495-500.

YANG Xuxu, JING Hongwen, CHEN Kunfu, et al. Study on influence law of in-situ stress in deep underground rocks on the size of failure zone in roadway[J]．Journal of Mining & Safety Engineering,2013,30(4): 495-500.

[7]蒋景东.深部软弱围岩流变应力恢复法地应力测试与分析方法研究[D].武汉:武汉大学，2016.

[8]康红普，司林坡，张晓.浅部煤矿井下地应力分布特征研究及应用[J].煤炭学报，2016，41(6):1332-1340.

KANG Hongpu, SI Linpo, ZHANG Xiao. Characteristics of underground in-situ stress distribution in shallow coal mines and its applications[J].Journal of China Coal Society,2016,41(6):1332-1340.

[9]李远，王卓，乔兰，等.基于双温度补偿的瞬接续采型空心包体地应力测试技术研究[J].岩石力学与工程学报，2017，36(6):1479-1487.

LI Yuan, WANG Zhuo, QIAO Lan, et al.Development of CSIRO cell with the compromised application of instantaneous data-logging，no-power data-connection and twin temperature compensation techniques [J].Chinese Journal of Rock Mechanics and Engineering,2017,36(6):1479-1487.

[10]宋林.节理岩体中应力波传播的动力特性研究[D].西安：西安建筑科技大学，2012.

[11]刘鸿文. 高等材料力学[M].北京：高等教育出版社，1985.

[12]钱鸣高，石平五，许家林.矿山压力与岩层控制.第2版[M].徐州：中国矿业大学出版社，2010.

[13]衡帅，杨春和，李芷，等.基于能量耗散的页岩脆性特征[J].中南大学学报(自然科学版)，2016，47(2):577-585.

HENG Shuai, YANG Chunhe, LI Zhi, et al. Shale brittleness estimation based on energy dissipation[J].Journal of Central South University(Science and Technology),2016,47(2):577-585.

[14]谢和平，彭瑞东，鞠杨.岩石变形破坏过程中的能量耗散分析[J].岩石力学与工程学报，2004，23(21):3565-3570.

XIE Heping, PENG Ruidong, JU Yang.Energy dissipation of rock deformation and fracture[J].Chinese Journal of Rock Mechanics and Engineering,2004，23(21):3565-3570.

[15]赵忠虎，鲁睿，张国庆.岩石破坏全过程中的能量变化分析[J].矿业研究与开发，2006，26(5):8-11.

ZHAO Zhonghu, LU Rui, ZHANG Guoqing.Analysis on energy transformation for rock in the whole process of deformation and fracture[J].Mining R & D,2006,26(5):8-11.

[16]常红，赵子龙.材料力学.II[M].北京：科学出版社，2012.

[17]李振雷.厚煤层综放开采的降载减冲原理及其工程实践[D].徐州：中国矿业大学，2016.