基于D-P准则的煤层钻孔封孔深度分析*

许克南，王佰顺，朱京京,2，郑明亮

(1. 安徽理工大学 能源与安全学院，安徽 淮南 232001；2. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，湖北 武汉 430071 )

0　引言

我国《煤矿瓦斯抽放规范》要求顺层钻孔的封孔深度为5～8 m，《防治煤与瓦斯突出规定》要求顺层钻孔的封孔段深度不得小于8 m[1-2]，因此大部分煤与瓦斯突出矿井把封孔深度确定为8 m。由于各煤岩巷道的参数(中间主应力、残余黏聚力、内摩擦角和剪胀角)以及支护应力不同导致部分矿井在相同封孔长度下瓦斯抽放效果不好，因此，确定适合本煤层的钻孔封孔深度是决定瓦斯抽放效果的关键[3-6]。

当煤岩巷道开挖之后,其周边会存在一个煤岩性质较差的破裂区，如果封孔长度不够且处在卸压区内, 则在抽采负压的作用下, 瓦斯会通过破裂区的煤层裂隙带和外部的煤巷空间连通导致瓦斯泄漏，从而降低瓦斯抽放浓度和纯度[7]。如果封孔长度过长，处于塑性区的应力集中带，则在其应力集中区域会形成封堵屏障，阻碍破裂区与塑性应力集中区两侧瓦斯的流动，为此钻孔的封孔长度应大于破碎区半径小于塑性区应力峰值点[8]。目前，确定煤层钻孔封孔深度的方法主要有现场实践法和理论计算法。现场测试法主要有钻屑量法和钻屑解析指标法，其中钻屑量法是通过向巷帮打钻，利用单位长度钻孔钻屑量的变化规律来确定钻孔合理封孔深度；钻屑解析指标法是指把含瓦斯煤样瞬间暴露于空气中，利用解析原理测定单位质量的煤样在不同时刻的瓦斯解析速度，通过钻屑瓦斯解析指标值K1来判定钻孔封孔深度。在理论计算方面，前人主要通过Airey，Fenner和Kastner公式确定钻孔封孔深度，Airey公式认为煤体破裂后，瞬间降低为残余强度，忽略煤岩体的流变性和残余黏聚力导致封孔深度偏大；Fenner和Kastner公式适用于完整性较好的围岩，把煤体视为理想的弹塑性介质，忽略了煤体的剪胀性和中间主应力，导致计算结果偏小。因此，要想确定合理的封孔深度，需要建立考虑中间主应力和煤岩剪胀角钻孔封孔模型[9-14]。

1　理论分析

1.1　圆形巷道开挖力学模型

由图1煤岩全应力-应变曲线可知，煤岩开挖的变形分布为破裂区(s区)，塑性区(p区)及弹性区(e区)(见图2)。当煤岩抗压强度不满足屈服条件，为弹性状态；当煤岩抗压强度满足屈服条件时为塑性状态；当围岩塑性应变达到破裂变形，为破裂状态。由此建立开挖力学模型如下：圆形开挖巷道半径为a,破裂区半径为Rs，塑性区半径为Rp，围岩位移为μ；围岩的支护力为Pi,原岩应力为σo，围岩的径向和环向应力分别为σθ和σr，应变为εr和εθ。为了便于计算，破裂区，塑性区和弹性区分别对应下标s，p和e。

图1　煤岩全应力—应变曲线Fig.1　Complete stress-strain curve of coal

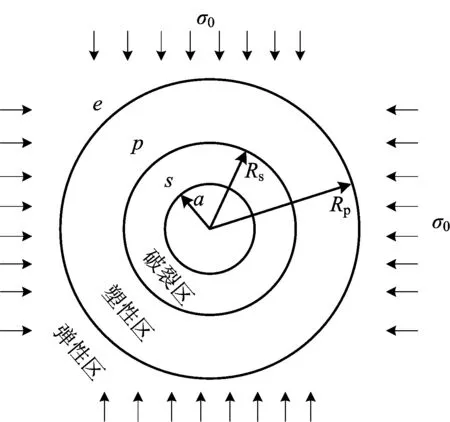
图2　圆形巷道力学模型Fig.2　Mechanical model of circular tunnel

1.2　D-P准则

D-P准则是由Mises准则线性演绎出来[15]，考虑了静水平压力及中间主应力对于煤岩体的影响，其表达式为:

(1)

式中:I1为第1应力不变量，J2为第2应力偏量不变量。如果定义σ1为最大主应力，σ2为中间主应力，σ3为最小主应力，得到I1和J2的屈服函数表达式为:

I1=σ1+σ2+σ3

(2)

(3)

关于平面应变问题，D-P准则实验参数kG和β与黏聚力c和内摩擦角φ之间的关系如下:

(4)

为了便于工程计算，通常利用主应力系数n表示σ1，σ2和σ3三者之间的关系：

n=(σ2-σ3)/(σ1-σ3)

(5)

其中0≤n≤1,n越小，表明中间主应力的作用越小；n越大，表明中间主应力发挥的作用越大。

将式(5)分别带入(2)和(3)式得：

I1=(1+n)σ1+(2-n)σ3

(6)

(7)

把式(6)和式(7)带入式(1)可得到D-P准则的函数表达式:

G=(λn-nβ-β)σ1-(λn+2β-nβ)σ3-

kf=0

(8)

当pi<σ0时，巷道周边围岩应力满足以下关系：

σ1=σθ，σ2=σz，σ3=σr

式中：σθ，σr，σz分别为环向应力、径向应力、轴向应力，同时满足σθ≥σz≥σr；把(8)式带入式得到关于极坐标的D-P准则表达式：

G=σθ-Mi,φσr-Ni,φ=0

(9)

式中：Mi,φ，Ni,φ是关于内摩擦角φ和黏聚力c相关的参数：

(10)

(11)

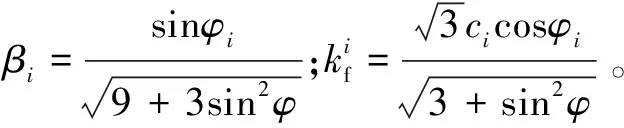
1.3　破裂区扩容系数

煤岩的塑性变形服从非线性流动规律，利用塑性函数Γ进行描述，由于其函数表达式与屈服函数G相同，因此仅用剪胀角Ψ把内摩擦角c替换之后得到塑性破裂区函数表达式：

Γ(σθ,σr)=σθ-Mi,ψσr

(12)

式中：Mi,ψ为剪膨胀角Ψ替换内摩擦角c之后的材料参数。根据破裂区位势理论得：

(13)

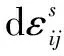
根据上式可得破裂区最大与最小应变增量：

(14)

(15)

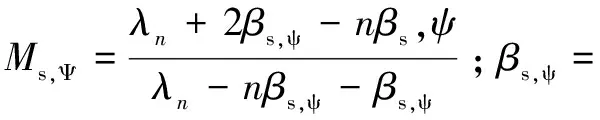
利用最小塑性主应变与最大塑性主应变之比，再结合式 (14)和(15)得到破裂区扩容系数为：

ξs=As,ψ

(16)

其中Ψs为破裂区剪胀角，在非关联法则下ψs≈φs/2[15]。

2　巷道煤岩的弹塑性分析

2.1　基本方程

各区满足的平衡微分方程为：

(17)

几何方程为：

(18)

根据非关联定律，得出破裂区和塑性区的本构方程为：

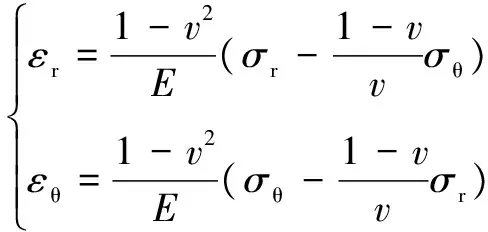
(19)

边界及接触条件：

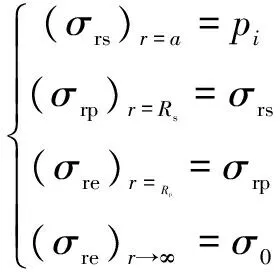
(20)

式中：u为径向位移；r为极径；E为弹性模量；v为泊松比。

2.2　弹性区应力应变分析

1)弹性区应力

(21)

式中：σRp为弹塑性交接处径向接触力。

当r=Rp把式(10)，(11)，(21)代入(9)式得：

σRp=(2σ0-Np,φ)/(Mp,φ+1)

(22)

2)弹性区应变及其位移

把(21)，(22)代入(19)中，得到弹性区应变表达式：

εre=D(Rp/r)2；εθe=-D(Rp/r)2

(23)

其中，D=(σRp-σo)/2G

2.3　塑性区应力应变

把式(9)，(10)，(11)代入(17)，结合边界条件，得到塑性区应力表达式

(24)

其中，Q=Np,φ/(Mp,φ-1)

塑性区的总应变由弹性应变和塑性应变2部分组成：

(25)

塑性区塑性应变关系为

(26)

通过式(18)，(23)和(25)，结合边界条件，可以得出塑性区应变及位移表达式：

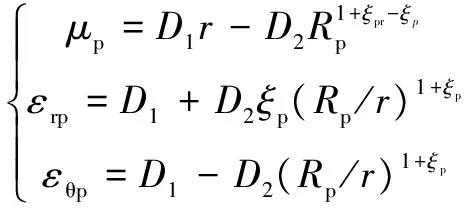
(27)

式中：D1=(1-ξp)D/(1+ξp)；D2=2D/(1+ξp)

2.4　破裂区应力应变

把式(9)，(10)，(11)代入方程(17)，结合边界条件，得到破裂区应力：

(28)

其中，T=Ns,φ/(Mp,φ-1)

由于破裂区总应变仅有塑性应变组成，可得破裂区环向和径向应变关系为：

εrs+ξsεθs=0

(29)

同样方法可得破裂区应变和位移为：

(30)

2.5　钻孔封孔深度解析式

当r=a时，巷道围岩表面位移

(31)

由式(20)，(24)，(28)得：

(32)

由于径向应变(εrs)r=Rs=(εrp)r=Rs位于的塑性区和破裂区交界处，因此结合式(27)和(30)，化简得：

(33)

联立(32)，(33)可得，破裂区半径为：

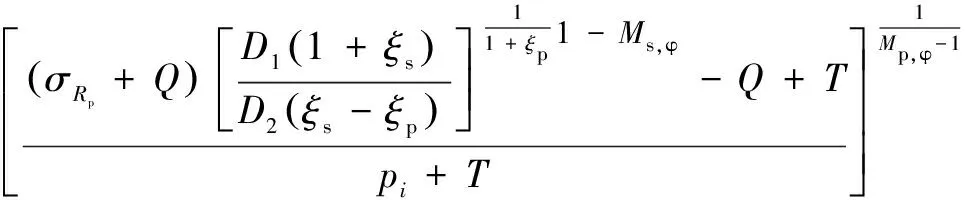
(34)

破裂区半径的表达式，即是煤层钻孔封孔深度的解析式。

3　煤层钻孔封孔深度的影响因素

3.1　煤层参数的测定

本次试验煤样取自张集矿某回采工作面的11煤，根据国际岩石力学学会规定，把煤样进行钻、切、磨，加工成φ50 mm×100 mm的标准试件[16]，进行编号(如图3)，然后在MTS815.03电液伺服机上进行原煤的三轴压缩试验，测定煤样基本参数见表1。

图3　 试验煤样Fig.3　Test coal sample

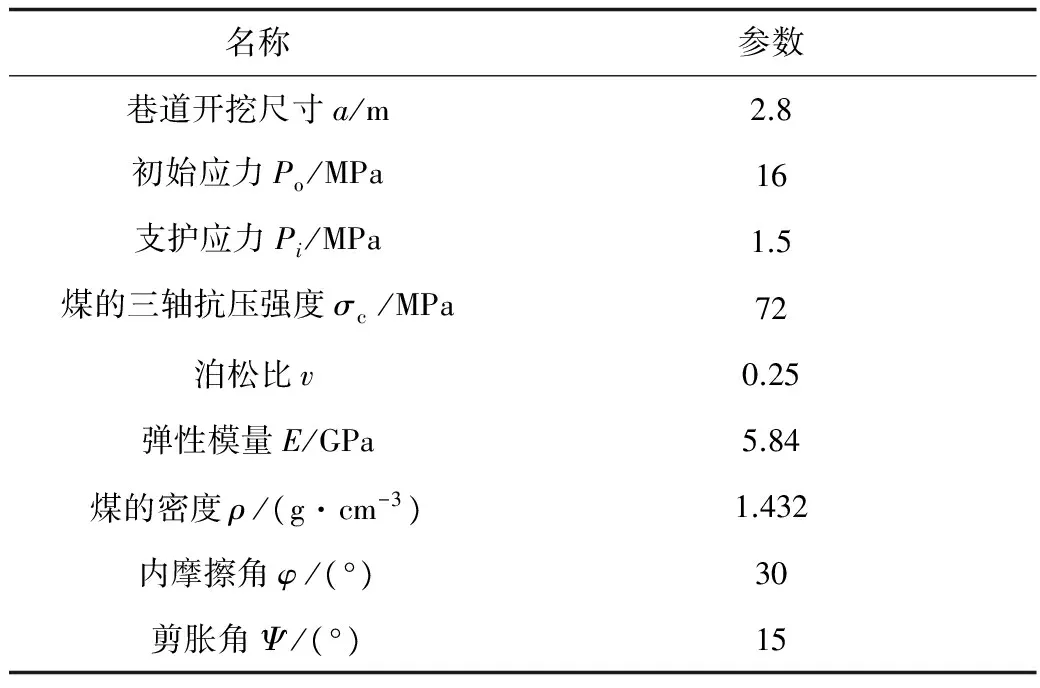
名称参数巷道开挖尺寸a/m2．8初始应力Po/MPa16支护应力Pi/MPa1．5煤的三轴抗压强度σc/MPa72泊松比v0．25弹性模量E/GPa5．84煤的密度ρ/(g·cm-3)1．432内摩擦角φ/(°)30剪胀角Ψ/(°)15

3.2　中间主应力和残余黏聚力对于煤层钻孔封孔深度的影响

由图4可以看出，当中间主应力系数一定时，随着残余黏聚力Cs从0.3 MPa增大到0.7 MPa，Rs/a也逐渐减小，并且当n=0.6时，Rs/a从3.2降低到2.8，降低了12.5%，并且此时是最小值，说明残余黏聚力越大破裂区半径越小，残余黏聚力越小破裂区半径越大，封孔深度越深，因此在进行瓦斯封孔深度时要考虑煤岩残余黏聚力的大小，残余黏聚力越大封孔越小，黏聚力越小封孔越深；当1≥n≥0.6时，随着中间主应力系数n的减小，Rs不断减小，当0.6≥n≥0时，随着中间主应力系数n的不断降低Rs不断扩大，因此可以得到中间主应力系数是影响破裂区半径的关键因素，所以在瓦斯封孔深度时，要考察中间主应力系数的大小。

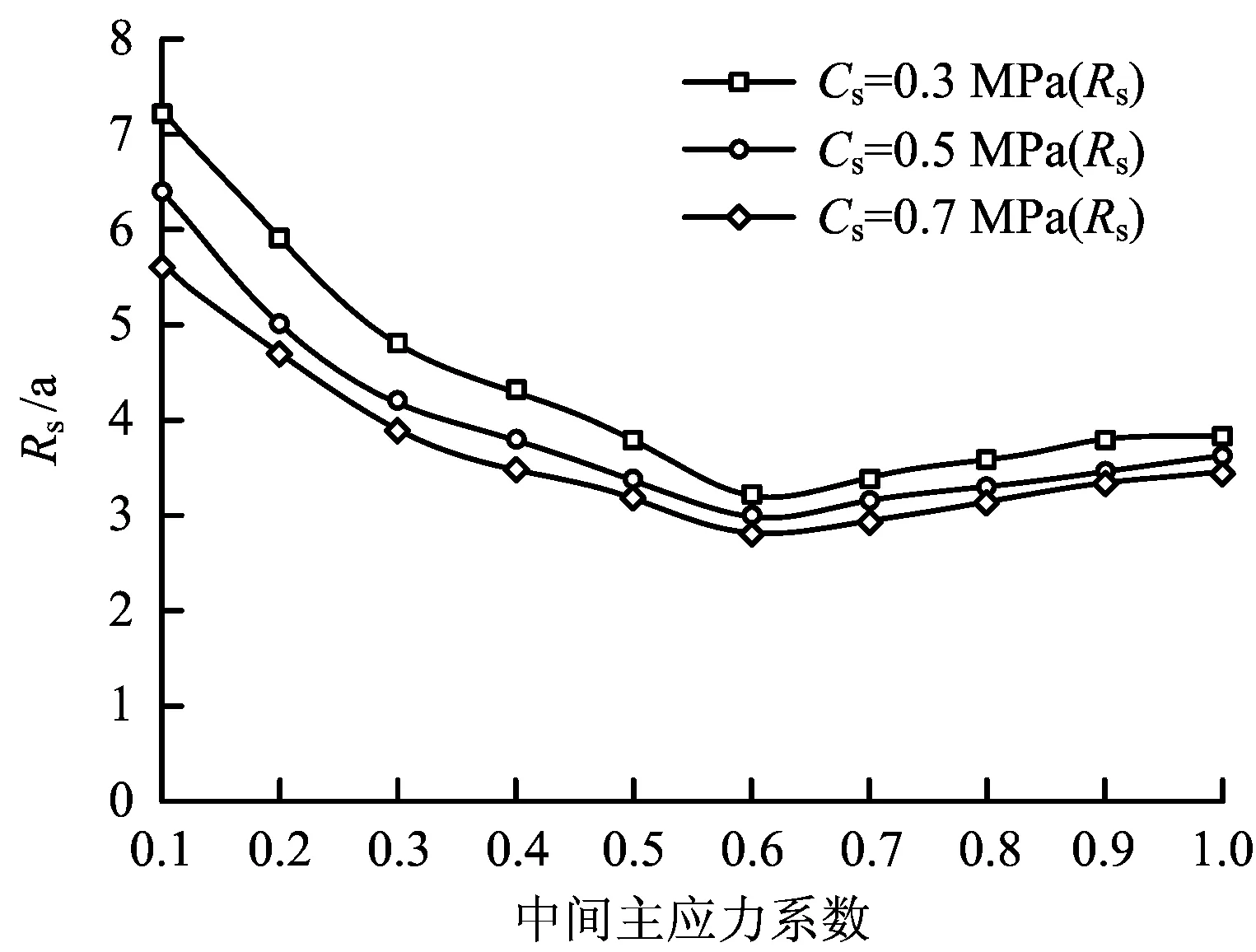
图4　中间主应力和残余黏聚力对钻孔封孔深度的影响Fig.4　Effect of intermediate principal stress and residual cohesion on borehole sealing depth

3.3　残余内摩擦角与剪胀角对于煤层钻孔封孔深度的影响

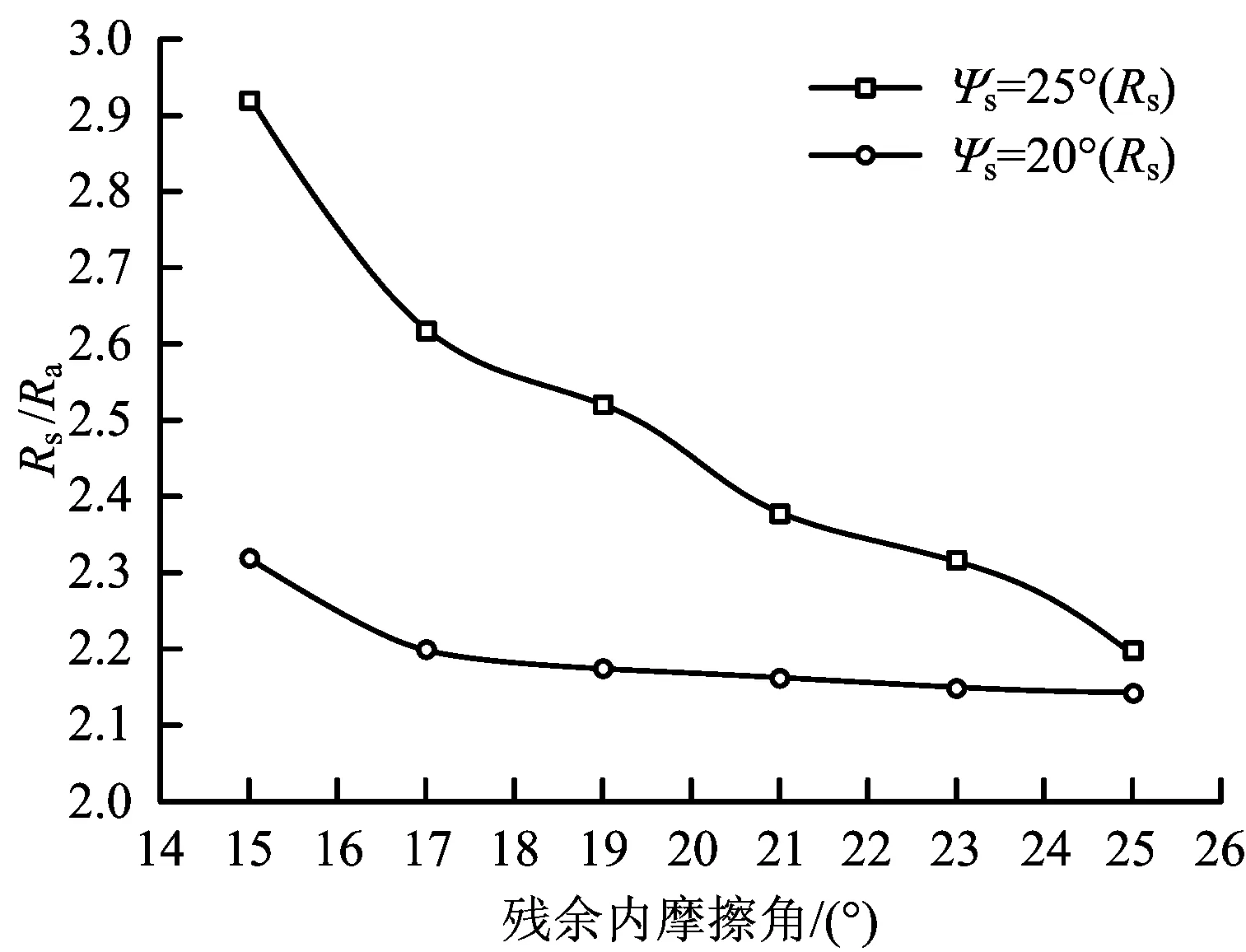
图5　剪胀角和残余内摩擦角对钻孔封孔深度的影响Fig.5　Effect of dilatancy angle and residual internal friction angle on borehole sealing depth

由图5可以看出，当Pi=1.5 MPa 时，Rs与破裂区剪胀角Ψs成正相关。当Ψs=25°时，残余内摩擦角φs从15°上升到25°，Rs/a减小0.72，表明随着煤岩残余内摩擦角的增大，破裂区半径Rs不断减小，钻孔封孔深度也不断减小；当煤岩残余内摩擦角一定时，随着剪胀角Ψs由20°增大到25°，Rs/a也随之增大，破裂半径也随着增大，钻孔封孔深度也不断增大，因此提高煤岩残余强度可以降低煤岩体体积膨胀，减小封孔深度，从而减少封孔材料。

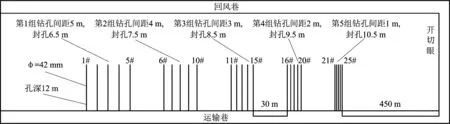
图6　钻孔布置示意Fig.6　Drilling arrangement diagram

4　工程实践

在淮南矿业集团某矿回采工作面进行现场试验，该煤巷工作面位于-550 m水平，初始应力为16 MPa，支护应力为1.5 MPa，巷道半径为2.8 m，把表1中的相关数据代入(32)式计算得出破裂区半径为7.36 m，考虑到安全因素，对瓦斯抽放钻孔的封孔深度确定为7.5 m，现采用平均瓦斯抽采法和钻屑量法进行验证。

在该工作面距离开切眼450 m选择5个地点进行试验，每个测点用直径为42 mm 的麻花钻杆钻机施工顺煤层钻孔，钻孔深度为12 m，钻完之后立即采用聚氨酯进行封孔(如图6所示)，钻进过程中测定钻屑量和平均瓦斯抽采浓度，根据测定结果绘制不同钻孔深度下钻屑量特征曲线图和平均抽采瓦斯浓度表，如图7和表2所示。

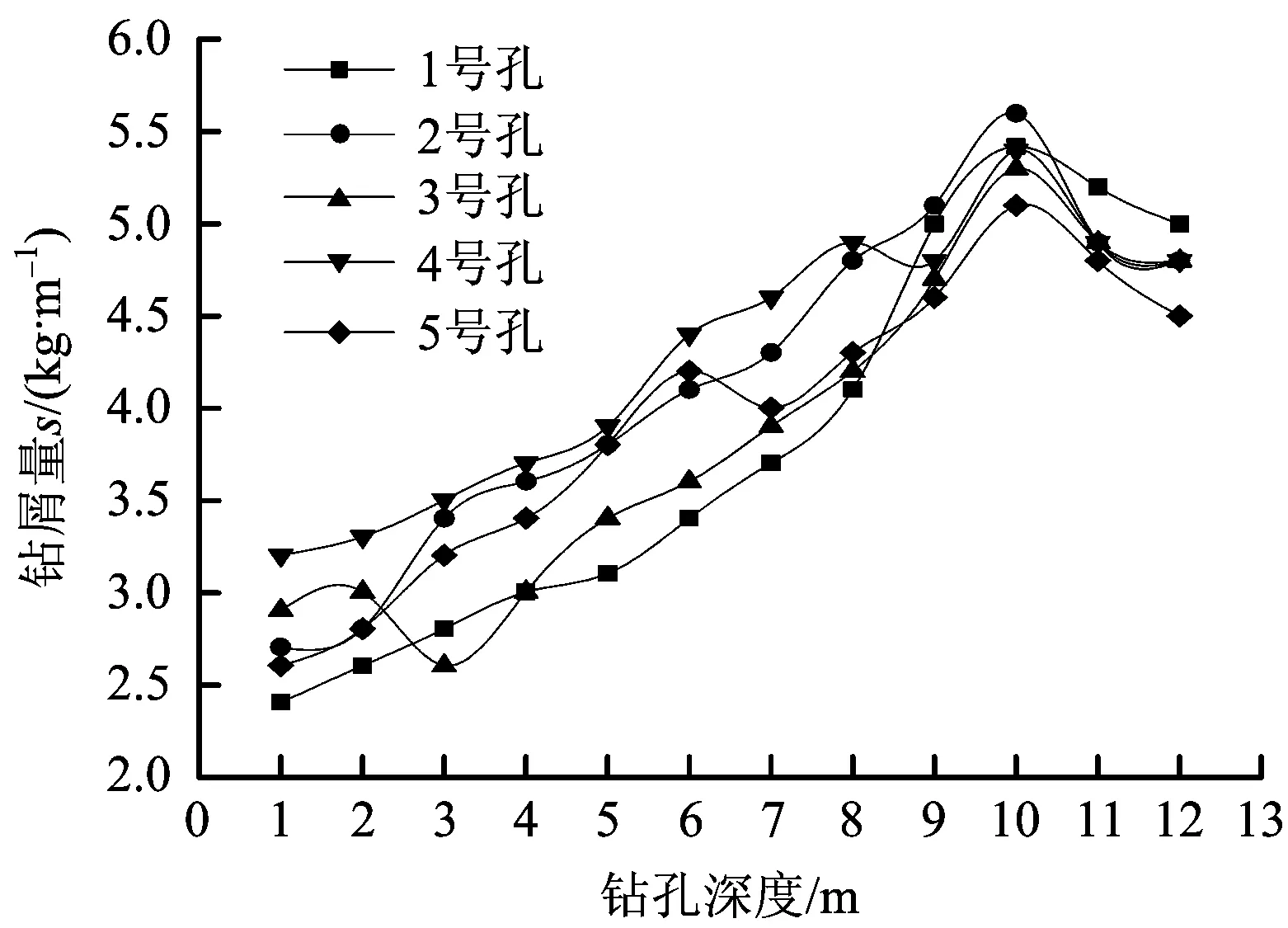
图7　钻屑量s与钻孔深度变化曲线Fig.7　The change curve of drilling cutting s and drilling depth

钻孔封孔深度/m6．57．58．59．510．5平均瓦斯抽采浓度/%18．631．434．838．139．3

由图7可以看出，钻屑量S在1～7 m之间增加的比较缓慢，这是由于卸压区内的煤体应力低于煤体的原始应力使得该区域钻屑量较少；钻屑量S在过了7～7.5 m之后增加幅度快速变大，并且在9.5 m时达到了峰值；钻屑量S在10～12.5 m之间个别数据点出现浮动，但总体呈现平稳下降的趋势，同时9.5 ～12.5 m的钻屑量的最小值仍然比1～7.5 m钻屑量要大。因此可以判定1～7.5 m为卸压区，也即是破裂区；7.5～9.5 m为应力升高区，9.5～12.5 m为应力集中区的应力下降区，出现应力峰值的位置约为9.5 m。由此可以确定钻孔封孔为7.5 m，与上述公式计算得出的结果7.36 m相差不大，因此通过钻屑量测定结果可以看出确定的煤层瓦斯钻孔封孔深度较为合理。

由表2可以得出，在抽采时间同样的条件下，钻孔封孔深度越深，平均抽采瓦斯浓度越大，封孔效果越好。在抽采40 d之后，封孔深度由6.5 m增大到7.5 m，平均抽采瓦斯浓度从18.6%猛增到 31.4%，增加了12.8%；封孔8.5，9.5，10.5 m的体积分数从31.4%增大到了39.3%，仅仅增大了7.9%，说明1～7.5 m是破裂区；封孔从9.5 m增大到10.5 m时，平均抽采瓦斯浓度仅增大了1.2%，这是由于10.5 m 的封孔长度已超出了应力最高点的深度，导致卸压区终端与应力最高点之间由于应力过于集中使得该段煤岩裂隙的透气性下降，形成屏障，阻隔了该区域煤体瓦斯的流动，因此平均瓦斯体积分数下降较慢，考虑到钻孔工艺与成本，合理的瓦斯抽采钻孔封孔深度为7.5 m，这与上式计算的结果一致。

5　结论

1)基于D-P屈服准则，对煤岩开挖巷道周围进行了弹塑性分析，并且考虑中间主应力系数和剪胀角推出了煤层钻孔周围应力应变和封孔深度解析式，得到煤岩体中间主应力、残余黏聚力、内摩擦角和剪胀角对于封孔深度有重要影响。

2)封孔深度与中间主应力表现出明显的区间关系，在一定范围内，封孔深度随中间主应力的增大而减小，当数值超过某一值时，随着中间主应力的减小而增大，因此，在煤层埋藏深度较深的矿井，封孔深度应适当增加。

3)对于质地较软的煤层，其煤体的剪胀角和扩容系数都会增大，造成煤巷破裂区半径的扩大，因此要适当增加封孔深度。

4)在淮南矿业集团某矿回采工作面进行了现场实践，通过计算得到该煤巷的封孔深度为7.36 m，通过钻屑量法和平均瓦斯抽采法进行验证，确定封孔深度的准确性。

[1]国家安全生产监督总局.煤矿瓦斯抽放规范：AQ10272006[S]. 北京:煤炭工业出版社, 2006.

[2]国家安全生产监督管理总局. 防治煤与瓦斯突出规定[M].北京: 煤炭工业出版社, 2009:20-30.

[3]周福宝, 王鑫鑫, 夏同强. 瓦斯安全抽采及其建模[J]. 煤炭学报, 2014,39(8):1659-1666.

ZHAO Fubao, WANG Xinxin, XIA Tongqiang. A model of safe drainage of coal seamgas[J]. Journal of China Coal Society, 2014,39(8): 1659-1666.

[4]徐龙仓. 提高煤层气抽采钻孔封孔效果研究与应用[J]. 中国煤层气,2008(1):23-25.

XU Longcang. Study onimproving the sealing effect of CMM drainage boreholes and itsapplication[J]. China Coalbed Methane, 2008(1): 23-25.

[5]韩颖, 张飞燕, 程虹铭. 基于灰关联分析的顺层钻孔瓦斯抽采有效半径主控因素研究[J]. 中国安全生产科学技术,2015,11(6):44-49.

HAN Ying, ZHANG Feiyan, CHENG Hongming. Research on main controlling factors of effective radius for gas extraction using hole drilled along seam based on grey relational analysis[J].Journal of Safety Science and Technology, 2015,11(6): 44-49.

[6]董贺, 王佰顺, 李春亭. 穿层预抽钻孔倾角与煤层气抽采效果关系的研究[J]. 中国安全生产科学技术, 2015,11(2):99-104.

DONG He, WANG Baishun, LI Chunting. Tudy on relationship between angle of penetration boreholes for predrainage in coal seam and gas drainage effect[J]. Journal of Safety Science and Technology, 2015,11(2): 99-104.

[7]蒋斌松, 张强, 贺永年,等. 深部圆形巷道破裂围岩的弹塑性分析[J]. 岩石力学与工程报,2007(5):982-986.

JIANG Binsong, ZHANG Qiang, HE Yongnian, et al. Elastoplastic analgsis of carcked surrounding rocks in deep circular openings[J]. Chinese Journal of Rock Mechanics and Engineering, 2007(5):982-986.

[8]武炜, 王兆丰. 钻孔封孔注浆压力及封孔深度数值模拟研究[J]. 煤炭科学技术,2015,43(11):68-72.

WU Wei, WANG Zhaofeng. Numerical simulation study on grouting pressure and borehole sealing depthof boreholesealing[J]. Coal Science and Technology,2015,43(11):68-72.

[9]JF Zou, SS Li, Y Xu, HC Dan, LH Zhao.Theoretical solutions for a circular opening in an elasttle-plastic rock mass incorporating the out-of-plane stress and seepage force[J].Ksce Journal of Civil Engineering,2016,20(2):687-701.

[10]KH Park, YJ Kim. Analytical solution for a circular opening in an elastic-brittle-plastic rock International[J].Journal of Rock Mechanics and Mining Sciences,2006,43(4):616-622.

[11]SK Sharan. Exact and approximate solutions for displacements around circular openings in elastic-brittle-plastic Hoek-Brown rock[J].International Journal of Rock Mechanics and Mining Sciences,2005,42(4):542-549.

[12]张小波, 赵光明, 孟祥瑞. 考虑峰后应变软化与扩容的圆形巷道围岩弹塑性D-P准则解[J].采矿与安全工程学报,2013,30(6):903-910.

ZHANG Xiaobo, ZHAO Guangming, MENG Xiangrui. Elastoplastic solution for surrounding rock of circular roadway based on D-P criterion by considering post-peak strain softening and dilatancy[J]. Journal of Miningand Safety Engineering, 2013,30(6): 903-910.

[13]张强, 王红英, 王水林, 等. 基于统一强度理论的破裂围岩劣化弹塑性分析[J].煤炭学报,2010,35(3):381-386.

ZHANG Qiang, WANG Hongying, WANG Shuilin, et al. Deterioration elasto-plastic analysis of cracked surrounding rocks based on unified strength theory[J].Journal of China Coal Society, 2010,35(3): 381-386.

[14]刘恺德. 高应力下含瓦斯原煤三轴压缩力学特性研究[J]. 岩石力学与工程学报,2017,36(2):380-393.

LIU Kaide. Mechanical properties of ram coal containing gas under high triaxal stress compression[J].Chinese Journal of Rock Mechanics and Engineering,2017,36(2):380-393.

[15]赵春风,杨砚宗,张常光,等. 考虑中主应力的常用破坏准则适用性研究[J]. 岩石力学与工程学报,2011,30(2):327-334.

ZHAO Chunfeng, YANG Yanzong, ZHANG Changguang, et al. Investigation on application of common failure criteria considering intermediate principal stress[J].Chinese Journal of Rock Mechanics and Engineering, 2011,30(2):327-334.

[16]刘恺德, 刘泉声, 朱元广, 等. 考虑层理方向效应煤岩巴西劈裂及单轴压缩试验研究[J]. 岩石力学与工程学报,2013,32(2):308-316.

LIU Kaide, LIU Quansheng, ZHU Yuanguang,et al. Experimental study ofcoal considering directivity effect of bedding plane under brazilian splitting and uniaxital compression[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(2):308-316.