基于题根研究下的函数与导数问题
2017-04-15 02:22:29福建省厦门松柏中学361012
数理化解题研究 2017年7期
福建省厦门松柏中学( 361012)
卢云辉●
基于题根研究下的函数与导数问题
福建省厦门松柏中学( 361012)
卢云辉●
本文对基于题根研究下的函数与导数问题进行一些整理与归纳,便于读者参考与借鉴.
一、基于重要习题研究下的函数与导数问题
人教A版选修2-2第32页B组第1大题第3小题,证明不等式:ex>1+x(x≠0).在此基础上拓展的习题: 当x>-1时,有x>-1 时,有x>ln( 1 + x) ; 当x>0 时,有x-x>lnx.


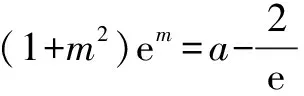
二、基于重要结论研究下的函数与导数问题
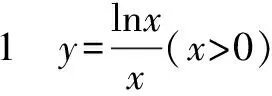
变式(1) 已知0 变式(2) 当a>1,b>1时,试比较ab-1与ba-1的大小. 例2 (2014年江苏高考·理19改编)已知函数f(x)=ex+e-x,其中e是自然对数的底数. 例3 已知函数f(x)=lnx-mx(m∈R).若f(x)有两个零点x1,x2,求证:x1x2>e2. 点评 这类问题涉及函数的零点、方程的根、曲线上的点,经过变形、构造后采用结论2使问题获得解决. 让学生成为解题高手的策略是:学习解题理论、经历解决难题、回顾解题过程、展示解题过程,最为重要的是让每个学生都要建立自已的解题体系. G632 B 1008 - 0333( 2017) 07 - 0047 - 01

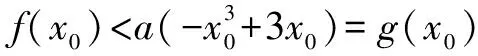

猜你喜欢
中学生数理化·七年级数学人教版(2020年12期)2021-01-18 06:57:42
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27 03:04:28
数理化解题研究(2020年13期)2020-05-07 03:29:02
数学物理学报(2019年5期)2019-11-29 07:46:30
新高考·高一数学(2018年5期)2018-11-22 11:03:52
新高考·高二数学(2017年5期)2018-03-16 21:13:21
中学生数理化·七年级数学人教版(2017年3期)2018-01-20 12:45:51
新高考·高一数学(2016年4期)2016-12-02 03:52:40
求学·理科版(2016年11期)2016-11-29 19:34:24
高中生·天天向上(2016年9期)2016-11-22 09:10:34

