应用题解决方法探讨

郭利娃

摘 要 小学数学应用题的解决方法有很多，在实际的应用题教学中，教师必须关注学生的解决方式的培训，还要积极促进学生的发展和增强学生的综合能力，指引学生自主解决应用题，创造更多的机会让学生交流应用题的解决方法，增强解题方法的训练，最后增强学生的解题能力。

关键词 小学数学 应用题 解决方法

中图分类号：G622 文献标识码：A 文章编号：1002-7661（2017）08-0068-02

在小学数学课程中，应用题与现实情况联系紧密，生动地反应现实世界的数量关系，是否能够从具体问题中将数量关系归纳出来，体现了一个人分析问题和解决问题的实际能力。本人结合自身多年的教学经验，针对应用题解决方法具体谈以下几点：

一、综合法

综合法是由条件出发，对可以解决的问题进行寻找，一般称为由因导果。在复合应用题中若寻找的问题为所求问题的充要条件，就说明已经将解决问题的关键找到。如例题：某服装厂计划做1200件上衣。前3天每天做120件，以后要将工作效率提高，每天做140件。完成计划总共需要多少天？

运用综合法解题，具体思路如下：工作已经做了3天，每天完成120件，可据此求出已经做的件数。已知总共要做1200件和已经做的件数，就能求出还没有做的件数。已知还没有做的件数和以后每天做140件，可求出还要做的天数；已知做了3天和还要做的天数，就能得到完成计划总共需要的天数。

二、分析法

分析法是以问题为思维起点，逐步向条件推进。一般称为执果索因。在复合应用题中，由问题想到条件，若此条件是由题目中的已知条件求出的，就说明已经将解决问题的关键找到。如例题：三年级有男生30人，女生是男生的2倍，求四年级一共有多少名学生？

运用分析法解题，具体思路如下：要求一共有多少名学生，需要知道男生人数（50人）和女生人数。要求女生人数，就需要知道男生人数（50）与倍数（2倍）。

三、公式法

对于涉及某些特定概念的应用题，学生因为生活经验的缺乏，往往会产生很大困难。在教学中一定要求学生逐个明确每个已知数据所对应的数学名称，然后选定一个名称，利用公式把已知数据连接起来，形成一个等式。比如，行船问题：一只船顺水行320千米需用8小时，水流速度为每小时15千米，这只船逆水行这段路程需用几小时？

解：由条件知，顺水速=船速+水速=320，而水速为每小时15千米，所以，船速为每小时320-15=25（千米）

船的逆水速为25-15=10（千米）

船逆水行这段路程的时间为3200=32（小时）

答：这只船逆水行这段路程需用32小时。

四、画图法

由题目中给出的条件画出与题意相符的示意图。通过观察分析图形，探索解决问题的方法。如例题：甲、乙两辆汽车同时从东、西两城相向而行，甲车每小时行42千米，乙车每小时行35千米，经过若干小时后，两车在离中点14千米处相遇。求两城之间的路程是多少千米？

运用画图法解题，具体思路如下：先依照题意，画出如下线段图：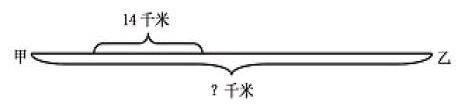

由图可看出：两车相遇时，甲车比乙车多行了2个14千米，即14=28（千米）。又知甲车每小时比乙车多行42-35=7（千米），所以可求出两车相遇时所用的时间是28=4（小时）。这样便能够求出两城之间的路程是：（42+35）=308（千米）。综合算式为：（42+35）€譡14€鳎？2-35）]=308（千米）。

五、假设法

在《孙子算经》这部古代数学名著中记载着鸡兔同笼的问题，这类问题就是应用假设法进行解题。假设法的应用范围较广，如例题：甲乙两个仓库内原来共存货物480吨，现在甲仓又运进其所存货物的40%，乙仓又运进其所存货物的25%，此时两仓共存货物645吨。求原来两仓各存货物多少吨？

此题中的百分率40%和25%的单位“1”是不同的，也不具备转化的条件，故需要运用假设法来分析解题：

假设两个仓库都运进所存货物的40%，则可知共运进货物4800%=192吨，但实际两仓共运进货物645-480=165吨，可知多算了192-165=27吨，为什么多算了27吨呢？这是因为乙仓实际运进了所存货物的25%也当作运进所存货物的40%计算了。由此可知，乙仓运来所存貨物的40%与25%的差相当于27吨，这样就能够计算出乙仓原来所存货物的吨数。

解：4800%=192（吨）

645-480=165（吨）

192-165=27（吨）

27€鳎？0%-25%）=180（吨）

480-180=300（吨）

答：原来甲仓存货物300吨，乙仓存货物180吨。

这道题目也可以假设两仓都运进所存货物的25%，解题思路可参照以上所述。用假设法解题的思考方法是：根据解题的需要来假设已知条件，并由假设将矛盾引出，然后对矛盾产生的原因进行分析，把原因分析清楚，就可以解答出题目了。

以上是我在教学解应用题时的几点做法，当然解决应用题的方法还有很多，还需要结合学生的实际情况及时调整教学思路，及时改变教学方法，同时及时总结及时完善，及时提高，使自己的教学效果更加显著。要鼓励学生从不同角度，用不同思路，联系不同的相关经验，探索问题的多种解法。

参考文献：

[1]刘友红.浅议小学数学应用题的教学策略[J].当代教育论坛（教学研究），2010，（15）.

[2]杜慧慧.探究数学应用题“问题——建模——应用”教学模式[J].小学教学参考，2015，（29）.

（责任编辑 李 翔）