一类对数形式退缩抛物型方程组解的整体存在性与爆破

孙仁斌

(中南民族大学 数学与统计学学院，武汉 430074)

一类对数形式退缩抛物型方程组解的整体存在性与爆破

孙仁斌

(中南民族大学 数学与统计学学院，武汉 430074)

考虑了一类由对数函数产生的退缩抛物型方程组的初边值问题，利用逼近的方法得到了解的局部存在性．通过特征函数构造的上解得到了解整体存在的条件，利用特征函数得到了解在有限时刻爆破的条件及爆破时间的上限．

退缩抛物型方程组；局部解；整体解；爆破

本文考虑如下由对数函数产生的退缩抛物型方程组解的初边值问题：

(1)

其中Ω为RN(N≥1为正整数)中具有光滑边界∂Ω的有界区域，u0(x),v0(x)为Ω上非负连续可微函数，在∂Ω上，u0(x)=0,v0(x)=0，f(s),g(s)在s≥0时为非负连续可微函数，常数α,β>0.

对于抛物型方程与方程组在有界区域上的初边值问题解的存在性与爆破性的讨论已有很长时间了，早期的讨论是针对半线性方程与方程组进行，主要讨论整体解存在的条件以及当整体解不存在而在有限时刻发生爆破时对爆破时间上限的估计[1-4]．随着讨论的深入，对爆破点集的分布和爆破速率的估计也开始进行并逐步精确[5-7]；另一方面讨论的方程及方程组的复杂程度逐渐加大，从最初的半线性方程到后来的退缩方程[8-11]，再到不同耦合形式的方程组[12-14]，以及各种类型的退缩方程组[15,16]．对于退缩性是由幂函数引起的方程及方程组的讨论已有不少成果，文[15]中讨论的方程组是ut=vα(uxx+au),vt=uα(vxx+bv)，文[16]中讨论的方程组是ut=up(Δu+av),vt=vq(Δv+bu)，文[17]对文[16]中的方程组在无界区域上进行了讨论．

本文讨论的初边值问题(1)中，方程的退缩性是由对数函数引起，当u=0或v=0时，方程出现退缩．首先利用逼近的方法给出解的局部存在性，其次讨论解整体存在的条件，最后讨论解在有限时刻发生爆破的条件．

1 解的局部存在性

对于退缩抛物型方程组初边值问题解的局部存在性与唯一性，讨论的方法有几种，但基本相同，在此只简要介绍主要步骤，不作详细的证明．首先,构造一个近似的非退缩抛物方程组的初边值问题．对常数ε>0，考虑如下问题：

(2)

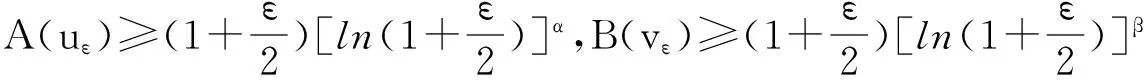
初边值问题(2)为非退缩的拟线性抛物型方程组，由经典的抛物型方程理论可知，其解是局部存在的，即存在σ>0，使问题(2)在Ω×[0,σ)上至少存在一个正解，仍记为(uε，vε),再由解的延展知，存在最大值Tε，使问题(2)在Ω×[0,Tε)上至少存在一个正解，且由极大值原理知uε≥ε,vε≥ε,于是(uε,vε)是如下初边值问题的解：

其次，由比较原理[18]，当ε1>ε2时，对应的解满足uε1≥uε2，vε1≥vε2，即(uε,vε)随ε的减少而减少，于是，存在T>0，当ε→0+时，Tε→T, (uε,vε)→(u,v)，由此得到问题(1)解的存在性．进一步通过经典的方法还可以得到解的唯一性[18]，即定理1.

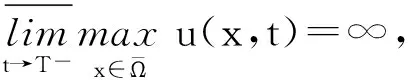
2 解的整体存在性

由比较原理[18]，容易得到下面的引理1.

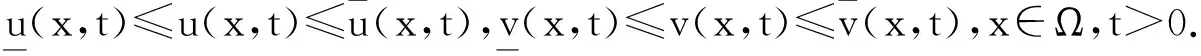
设φ(x)是特征值问题：

(3)

定理2 设存在正常数a,b和k,l，且al≤λ1k,bk≤λ1l，使函数f(s),g(s)满足：f(s)≤as，g(s)≤bs，s>0,函数u0(x),v0(x)满足u0(x)≤kφ(x)，v0(x)≤lφ(x)，x∈Ω,则问题(1)存在整体解．

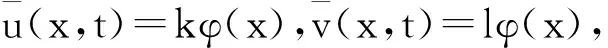
(1+kφ)[ln(1+kφ)]α(λ1kφ-f(lφ))≥

(1+kφ)[ln(1+kφ)]α(λ1kφ-alφ)≥0,

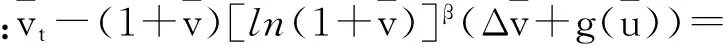
-(1+lφ)[ln(1+lφ)]β(lΔφ+g(kφ)),

利用(3)式，有：

(1+lφ)[ln(1+lφ)]β(λ1lφ-g(kφ))≥

(1+lφ)[ln(1+lφ)]β(λ1lφ-bkφ)≥0.

于是问题(1)存在上解(kφ(x)，lφ(x))，由引理1得u(x,t)≤kφ(x),v(x,t)≤lφ(x)对任意t>0都成立，故u(x,t),v(x,t)对任意t>0都有定义，证毕．

3 解的爆破性

引理2 设初值函数u0(x),v0(x)满足：

u0(x)≥φ(x),v0(x)≥φ(x)，

(4)

且存在常数a>λ1，b>λ1,使函数f(s),g(s)满足：

f(s)≥as,g(s)≥bs,s>0，

(5)

则问题(1)的解满足u(x,t)≥φ(x),v(x,t)≥φ(x),x∈Ω,t>0．

证明 令w(x,t)=u(x,t)-φ(x)，z(x,t)=v(x,t)-φ(x)，则t=0时，w≥0，z≥0,x∈∂Ω时，w=z=0，而x∈Ω,t>0时，wt=ut=(1+u)[ln(1+u)]α(Δu+f(v))=(1+u)[ln(1+u)]α(Δw+Δφ+f(v)),

利用(3)、(5)式，有：

wt=(1+u)[ln(1+u)]αΔw+(1+u)[ln(1+u)]α(f(v)-λ1φ)≥(1+u)[ln(1+u)]αΔw+(1+u)[ln(1+u)]α(av-λ1φ)=(1+u)[ln(1+u)]αΔw+(1+u)[ln(1+u)]α(az+aφ-λ1φ),

即有：wt≥(1+u)[ln(1+u)]αΔw+

(1+u)[ln(1+u)]αaz.

(6)

zt=vt=(1+v)[ln(1+v)]β(Δv+g(u))=(1+v)[ln(1+v)]β(Δz+Δφ+g(u)),

利用(3)、(5)式，有：

zt=(1+v)[ln(1+v)]βΔz+(1+v)[ln(1+v)]β(g(u)-λ1φ)≥(1+v)[ln(1+v)]βΔz+(1+v)[ln(1+v)]β(bu-λ1φ)=(1+v)[ln(1+v)]βΔz+(1+v)[ln(1+v)]β(bw+bφ-λ1φ),

即有：zt≥(1+v)[ln(1+v)]βΔz+

(1+v)[ln(1+v)]βbw.

(7)

由(6)、(7)式及抛物方程组的极大值原理知w≥0,z≥0，证毕．

v(x,t))-1[ln(1+v(x,t))]-βvt(x,t)φ(x)dx=

由(4)、(5)式得：

由引理2得：

[1] Weissler F.Existence and nonexistence of global solutions for a semilinear heat equations[J].Israel Journal of Mathematics,1981,38:29-40．

[2] Friedman A, Mcleod J B．Blow up of solutions of nonlinear degenerate parabolic equations[J].Archive for Rational Mechanics and Analysis,1987,96: 55-80．

[3] Friedman A, Mcleod J B．Blow up of positive solutions of semilinear heat equations[J].Indiana University Mathematics Journal,1985,34: 425-447．

[4] Caffarrelli L A, Friedman A.Blow-up of solutions of nonlinear heat equations[J].Journal of Mathematical Analysis and Applications,1988,129: 409-419．

[5] Liu W X.The blow-up rate of solutions of semilinear heat equations[J]． Journal of Differential Equations, 1989,77:104-122．

[6] Filo J.Diffusivity versus absorption through the boundary[J].Journal of Differential Equations, 1992, 99:281-305．

[7] Gage M E．On the size of the blow-up set for a quasi-linear degenerate parabolic equation[J].Contemporary Mathematics,1992,127:55-80．

[8] Chen H W.Analysis of blowup for a nonlinear degenerate parabolic equations[J].Journal of Mathematical Analysis and Applications, 1995,192: 180-193．

[9] Ding J T, Guo B Z．Blow-up and global existence for nonlinear parabolic equation with Neumann boundary conditions[J].Computers and Mathematics with Applications, 2010,60: 670-679．

[10] Payne L E, Philippin G A.Blow-up phenomena for a semilinear heat equations with nonlinear boundary condition, II[J].Nonlinear Analysis,2010,73: 971-978．

[11] Anada K, Ishiwata T．Blow-up rates of solutions of initial-boundary value problems for a quasi-linear parabolic equation[J].Journal of Differential Equations,2017, 262:181-271．

[12] Zheng S N.Global existence and global non-existence of solutions to a reaction-diffusion system[J].Nonlinear Analysis,2000,39: 327-340．

[13] Wang M X.Blow-up rate estimates for semilinear parabolic systems[J].Journal of Differential Equations, 2001, 170:317-324．

[14] Pedersen M, Lin Z G.The profile near blowup time for solutions of diffusion systems coupled with localized nonlinear reactions[J].Nonlinear Analysis,2002,50: 1013-1024．

[15] Duan Z W, Zhou L.Global and blow-up solutions for nonlinear degenerate parabolic systems with crosswise-diffusion[J].Journal of Mathematical Analysis and Applications, 2000,244: 263-278.

[16] Wang M X.Some degenerate and quasilinear parabolic system not in divergence form[J].Journal of Mathematical Analysis and Applications, 2002,274: 424-436．

[17] 孙仁斌．半空间上退缩抛物型方程组解的全局存在与爆破[J].中南民族大学学报(自然科学版),2007,26(1):94-96．

[18] Pao C V.Nonlinear parabolic and elliptic equations[M].New York: Springer,1992:381-458．

Global Existence and Blow-up for a Degenerate Parabolic System Come from Logarithmic Function

SunRenbin

(College of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China)

In this paper, a class of initial-boundary value problem of degenerate parabolic system come from logarithmic function was considered.The local existence of solution was proved by approximation method.The condition of global existence of the solution was obtained by the upper solution of the characteristic function, and the blow-up condition and the upper bound of the blow-up time were obtained by using the characteristic function.

degenerate parabolic system；local solution；global solution；blow-up

2017-01-04

孙仁斌(1964-)，男，副教授，研究方向：抛物型偏微分方程， E-mail: sunrenbin@foxmail.com

国家自然科学基金资助项目(61374085)

O175.26

A

1672-4321(2017)01-0119-04