基于并行相关向量机的多步预测方法研究

韩中合，周沛，苑一鸣

（华北电力大学能源与动力工程学院，河北保定 071003）

基于并行相关向量机的多步预测方法研究

韩中合，周沛，苑一鸣

（华北电力大学能源与动力工程学院，河北保定 071003）

针对风速时间序列的非线性和非平稳性的特点以及传统迭代法累计误差较大的不足，提出了基于并行相关向量机的多步预测方法。利用相空间重构进行样本重构，通过建立并行相关向量机（RVM）的短期风速预测模型对风速进行预测。仿真结果表明，与传统的多步预测模型相比，该方法预测精度更高。

相关向量机；多步预测；相空间重构

风能作为一种储量丰富、洁净环保、分布广泛的可再生清洁能源，其具有其他能源不具备的发展潜力和发展前景。随着风电场规模的扩大，风电在电网中所占比重不断增加，但由于风能具有间歇性、不可控性和波动性等特点，极大影响了电力系统的发电质量、安全性和稳定性[1]。因此，对风速进行准确的预测是解决这一问题的重要手段。

目前，风电场风速预测大多基于历史数据的方法，主要包括持续预测法、卡尔曼滤波法、随机时间序列法、人工神经网络法、模糊逻辑法以及一些组合方法[2-3]等，这些方法大多是基于单步预测进行建模[4-6]。对于多步预测，文献[7]提出了直接式预测模型来进行风速的多步预测，在预测过程中没有引入估计值，即没有产生累积误差，也即没有考虑到时间序列内在的相关性，可能会打破时间序列之间本质特性的延续性；文献[8]提出滚动式预测模型，该模型在一些预测中取得了不错的效果，但每一步产生的误差会向后传递，造成误差的累积，预测步数越多，累积的误差越大；文献[9]提出了直接-滚动式预测模型，同直接式预测模型一样，运用不同模型对每一步进行预测，每一步预测中都加入前几步的预测值，同样无法避免误差累积对结果的影响；相比于单步输出，文献[10]提出了多输出式预测模型，既可以克服直接式模型对时间序列的条件独立假设，又可以克服滚动式模型带来的迭代误差，但此方法泛化能力差；针对多步预测存在的问题，本文提出了基于并行相关向量机（P-RVM）的多步预测方法。该方法通过相空间重构得到的时间延迟对风速序列进行重构，对每步再进行RVM预测，在保证预测精度的同时大大提高了预测步长。

1 相关向量机

相关向量机[11]RVM）是通过核函数映射把数据由低维向高维空间转化的，相关向量机的训练是基于贝叶斯理论，在先验分布的条件下，利用自动相关决策理论（automatic relevance determination，ARD）来消除无关联的点，从而获得稀疏化的分类模型，算法不但稀疏性高，而且能够给出预测准确度的概率。

式中：目标函数带有噪声且满足εi～N（0，σ2）；wi为权重系数；k（x，x）i为核函数；N为样本数量。

由式（1）可知，求得ti服从ti～（y（xi，w），σ2）的分布。

对于相互独立的目标值t=[t1，t2，…，tn]T，在wi与σ2已知的条件下，训练集的似然估计如下：

式中：t=（t1，t2，…，tN）T；w=（w1，w2，…，wN）T；Φ为由特征向量代入到核函数中的N×（N+1）维矩阵：

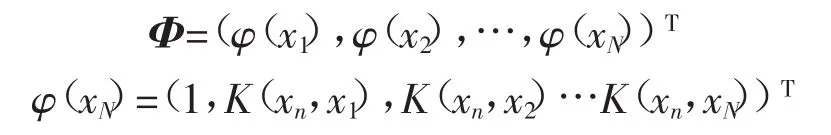
由于预测模型中参数众多，为了避免直接使用最大似然法得到w和σ2产生的过拟合现象[9]，对w加上先决条件，即采用稀疏贝叶斯原理对w赋予零均值高斯先验分布，得：

式中：α=[α1，α2，…，αn]T是N+1维超参数向量，每一个权重对应一个独立的超参数分量，因此将求解权重wi的问题转化为对αi的求解，并且保证了RVM的稀疏性。

在定义了先验概率分布及似然分布以后，根据贝叶斯原理，就以求得所有未知参数的后验概率分布为

使用最大似然法可得超参数α和方差σ2。对于新的输入值x*，与其对应的预测结果为y*=μTφ（x*）。

2 基于并行相关向量机的多步预测

单步迭代预测采用预测值来继续下一个值的预测，即通过预测得到的结果与之前数据构成时间序列，对下一个时间点的数据进行预测，这样做会随着被预测点的增加造成误差积累，造成预测结果与实际值偏差较大；而多步预测即对每一个时间序列进行单独预测，每一步仅产生一个预测值，从而很好地保证了预测精度。

针对文献[7-10]多步预测存在的预测计算量大、预测误差较大等问题，本文提出了基于并行相关向量机（P-RVM）的多步预测方法。在已知风速序列具有混沌特性的基础上[11-12]，该方法将已知风速时间序列分为τ个并列的时间序列，每个序列之间的关系是并列进行的。通过确定参数m对时间序列进行特征提取，从而确定被预测值。τ个并行相关向量机对应τ个预测值，将τ个预测值按时间顺序排列，就形成多步预测，即实现对风速的并行多步预测。因此τ与m的确定直接决定了风速时间序列的构造和模型的建立。

2.1 τ和m的确定及相空间重构理论

并行RVM个数（预测步数）与特征维数的选取不是任意的，τ的选取决定了预测的步数，即可预测时长；m的选取影响到样本的特征，进而决定了模型的预测精度。故需要对二者的选取进行研究。

本文从时间序列非线性动力学特性角度出发，基于混沌相空间重构理论计算确定τ与m的值。

相空间重构是为了对混沌时间序列进行判定与预测，根据Packard和Takens提出的嵌入理论[13]，如果嵌入维数m≥2d+1（d为系统动力学维数），则在此嵌入维数的重构空间里把有规律的轨迹恢复出来。在相空间重构过程中，对于嵌入维数与延迟时间的选取是否恰当，将直接影响时间序列的重构质量与预测精度。一般采用互信息法计算时间延迟τ，采用Cao方法计算重构相空间的嵌入维数m。

2.2 并行相关向量机的多步预测模型建立

对于时间序列X={X1，X2，…，Xn}，基于并行RVM多步预测的模型建立具体步骤如下：

1）确定时间延迟τ。从风场风速数据中选取合适数目的一组风速数据并分析其混沌特性，通过互信息法计算时间延迟τ。

2）利用τ将数据分组。以τ作为时间间隔将时间样本进行分组，最终将样本分为τ组：

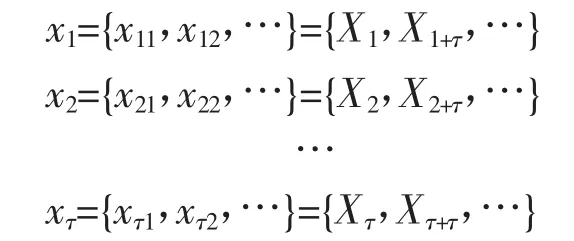
3）确定样本特征及目标值。采用Cao方法来对嵌入维数m进行计算，并将m作为特征维数，得到样本特征。以时间序列xi（i=1，2，…，τ）为例，构造样本特征，并与目标值对应：

其中，左侧为样本特征，右侧为对应目标值。即得到第i个时间序列的训练样本。

4）建立RVM预测模型。分别对每组时间序列进行样本训练，建立RVM预测模型。

5）形成多步预测结果。利用每个时间序列整合的样本特征，得到每个时间序列的最后一组样本特征对应的目标值yi，即为风速的预测值，对τ组的预测值进行有序的排列，最终形成多步预测的预测结果。如图1所示（y1、y2、…yτ即为多步预测结果）。PRVM多步预测流程图如2所示。

图1 时间序列并行多步预测Fig.1 Parallelmulti-step prediction of time series

3 多步预测模型应用研究

分别选取华北地区A、B风场间隔为20 min的样本容量为400个风速数据，对之后的8个测点的风速进行预测。

图2 P-RVM多步预测流程图Fig.2 Flowchart of themulti-step prediction ofw ind speed forecasting

采用2.1节提出的互信息法和Cao方法计算所取风速序列的时间延迟与嵌入维数，计算结果见表1。

表1 2个风速时间序列的τ和mTab.1 τand m of two w ind speed time series

根据时间延迟τ，将时间样本序列分为8组；利用嵌入维数4，构造样本特征维数，得到样本特征；建立P-RVM多步预测模型，即8个并行RVM预测模型；分别利用并行预测模型对未来数据点进行单步预测，最终形成8步预测结果，预测结果见图3—图4。

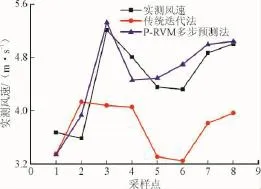
图3 2种方法预测结果对比Fig.3 Com parison of 2methods for prediction results

本文采用相对误差和平均相对误差来衡量传统方法与本文方法的精确度：

图4 2种方法预测结果对比Fig.4 Com parison of 2methods for prediction result

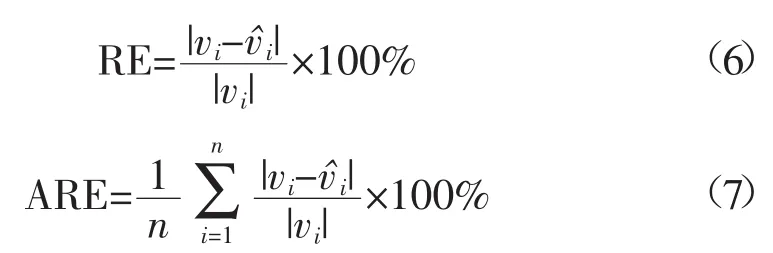
式中：vi、v^i分别为第i个实际风速与预测风速的值；n取8。

表2为预测的8个样本点的对比。从对比风场A、B的预测相对误差可以看出：基于P-RVM的多步预测方法的平均相对误差分别为5.386 3%、5.559 7%，而传统方法的平均相对误差分别为19.087 2%、15.997 1%。可以明显看出，基于并行相关向量机（PRVM）的多步预测方法的预测精度明显好于传统迭代法，预测值更接近真实值，满足风电场关于风速预测的误差精度要求[14-15]。

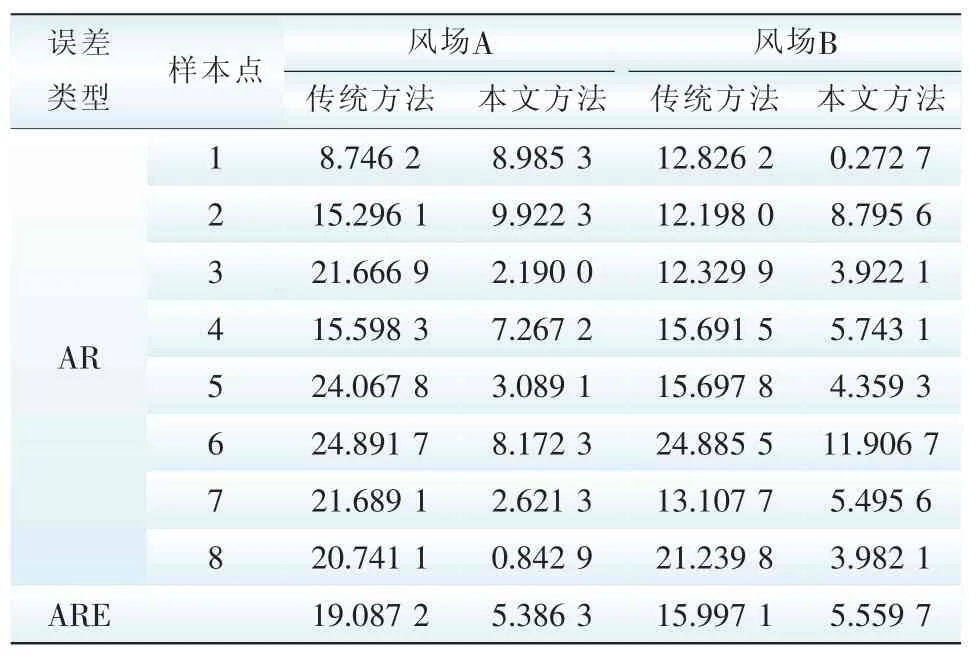
表2 风场风速预测结果对比Tab.2 Com parison of w ind speed forecasting results %

4 结论

本文针对风电机组风速预测问题，提出了基于并行相关向量机（P-RVM）的多步预测方法，进行短期风速预测，并得出以下结论：

1）RVM方法在对风速进行短期预测建立模型时不需要过多的模型参数，更容易建立预测模型。同时，该方法具有较强的小样本学习能力，在计算时不需要过多的样本参数，便于计算。

2）本文提出的P-RVM可以实现高精度多步预测，与传统多步预测方法相比避免了预测计算量大的问题，同时克服了迭代方法产生的迭代误差。

3）通过混沌相空间重构方法，从样本时间序列自身的动力学特性出发，计算得到时间延迟，即时间序列的可预测步数，为P-RVM可预测步数的选取提供了理论依据。

[1]雷亚洲，王伟胜，戴慧珠，等.风电对电力系统运行的价值分析[J].电网技术，2002，26（5）：10-14. LEI Yazhou，WANG Weisheng，DAI Huizhu，et al. Analysys ofwind power alue to power system operation[J]. Power System Technology，2002，26（5）：10-14（in Chinese）.

[2]杨秀媛，肖洋，陈树勇.风电场风速和发电功率预测研究[J].中国电机工程学报，2005，25（11）：1-5. YANG Xiuyuan，XIAO Yang，CHEN Shuyong.Wind speed and generated power forecasting in wind farm[J]. Proceedingsof theCSEE，2005，25（11）：1-5（in Chinese）.

[3]BOSSANYIE A.Short-term wind prediction using kalman filters[J].Wind Engineering，1985，9（1）:1-8.

[4]刘子俊，孙健.基于遗传算法和神经网络的分时段风速预测方法[J].江苏电机工程，2015，34（1）:6-8. LIU Zijun，SUN Jian.The wind speed prediction based on genetic algorithm and neural network with different periods[J].Jiangsu Electrical Engineering，2015，34（1）：6-8（in Chinese）.

[5]颜晓娟，龚仁喜，张千锋.优化遗传算法寻优的SVM在短期风速预测中的应用[J].电力系统保护与控制，2016，（9）：38-42. YAN Xiaojuan，GONG Renxi，ZHANG Qianfeng.Application of optimization SVM based on improved genetic algorithm in short-term wind speed prediction[J].Power System Protection and Control，2016（9）：38-42（in Chinese）.

[6]孙薇，刘默涵.基于改进最小二乘支持向量机的短期负荷预测[J].电力科学与工程，2015（12）：16-21，33. SUNWei，LIU Mohan.Short-term load forecasting based on improved least squares-support vector machine[J].Electric Power Science and Engineering，2015（12）：16-21，33（in Chinese）.

[7]COSKUN HAMZAÇEBI，DIYAR AKAY，FEVZIKUTAY. Comparison of direct and itera-tive artificial neural network forecast approaches in multi-periodic time series forecasting[J].Expert Systemswith Applications，2009，36（2）:3839-3844.

[8]孙春顺，王耀南，李欣然.小时风速的向量自回归模型及应用[J].中国电机工程学报，2008，28（14）：112-117. SUN Chunshun，WANG Yaonan，LI Xinran.A vector autoregressionmodel of hourly wind speed and its applications in hourly wind speed forecasting[J].Proceedings of the CSEE，2008，28（14）：112-117（in Chinese）.

[9]TAIEB，BOTEMPIS，SORJAMAA G，et al.Long-term prediction of time series by combining direct and mimo strategies[C].In International Joint Conference on Neural Networks，Atlan-ta，Georgia，2009（6）:14-19.

[10]TAIEB S B，SORJAMAA A，BOTEMPIG.Multiple outputmodeling formulti-step-ahead time series forecasting[J]. Neurocomputing，2010，73（10-12）：1950-1957.

[11]刘爱国，薛云涛，胡江鹭，等.基于GA优化SVM的风电功率的超短期预测[J].电力系统保护与控制，2015（2）：90-95. LIU Aiguo，XUE Yuntao，HU Jianglu，et al.Ultra-shortterm wind power forecasting based on SVM optimized by GA[J].Power System Protection and Control，2015（2）：90-95（in Chinese）.

[12]李占英，王科俊，张明君，等.基于混沌和二阶对角递归网络的船舶横摇的直接多步预测方法[J].控制与决策，2012，27（7）：1057-1065. LI Zhanying，WANG Kejun，ZHANG Mingjun，et al. Directmulti-step prediction approach of ship rolling based on chaotic and second order diagonal recurrent neural network[J].Control and Decision，2012，27（7）：1057-1065（in Chinese）.

[13]王丽婕，廖晓钟，高爽，等.并网型大型风电场风力发电功率-时间序列的混沌属性分析[J].北京理工大学学报，2007，27（12）：1077-1080. WANG Lijie，L IAO Xi a o z h o n g，G AO Shu a n g，etal.Chaos characteristics analysis of wind power generation time series for a grid connecting wind farm[J].Transactions of Beijing Institute of Technology，2007，27（12）：1077-1080（in Chinese）.

[14]柳玉，曾德良，刘吉臻，等.基于小波包变换的最小二乘支持向量机短期风速多步预测和信息粒化预测的研究[J].太阳能学报，2014，35（2）：214-220. LIU Yu，ZENG Deliang，LIU Jizhen，et al.Wavelet packet transform and the least squares support vector machine in research of short-term wind speed multistep prediction and information granulation prediction[J].Acta Energiae Solaris Sinica，2014，35（2）：214-220（in Chinese）.

[15]吕金虎，路君安，陈世华.混沌时间序列分析及其应用[M].武汉：武汉大学出版社，2002：46-80.

（编辑 董小兵）

Research on M ulti-Step Prediction Based on Parallel Relevance Vector M achine

HAN Zhonghe，ZHOU Pei，YUAN Yiming
（School of Energy and Power Engineering，North China Electric Power University，Baoding 071003，Hebei，China）

According to the characteristics of the nonlinear and non-stationary of wind speed time series and the large accumulation error of the traditional iterative method，this paper puts forward amulti-step predictionmethod based on a parallel relevance vectormachine.By using phase space reconstruction to reconstruct samples，short-term wind speed prediction is conducted by using parallel relevance vector machine（RVM）. Compared with the traditional multi-step prediction method，the simulation results show that the proposed method is more accurate than the traditionalmulti-step predictionmodel.

relevance vectormachine；multi-step prediction；phase space reconstruction

2016-04-29。

韩中合（1964—），男，博士，教授，研究方向为热力设备状态检测与故障诊断、两相流计算与测量；

周 沛（1992—），男，硕士研究生，研究方向为状态监测与故障诊断；

苑一鸣（1992—），男，硕士研究生，研究方向为状态监测与故障诊断。

中央高校基本科研业务费（2015MS102）；国家自然科学基金项目（51306059）。

Project Supported by the Central University Basic Scientific Research Program（2015MS10）；the National Nature Science Foundation of China（51306059）.

1674-3814（2017）02-0112-05

TM614

A