改进Bayesian后验比的异常风速值检测方法

陈伟，吴布托，裴喜平，王懿喆

（兰州理工大学电气工程与信息工程学院，甘肃兰州 730050）

改进Bayesian后验比的异常风速值检测方法

陈伟，吴布托，裴喜平，王懿喆

（兰州理工大学电气工程与信息工程学院，甘肃兰州 730050）

风电场运行数据中含有异常风速值，为了优化风电数据的质量，提出了组合预测与Bayesian后验比的异常值检测方法。为了降低预测误差，先对风速序列建立Adaboost-BP网络和EMD-LV-SVM的组合预测模型，利用预测值与测量值的偏差得到含有粗大误差的残差序列；为了提高检测方法的可靠性，采用Bayesian后验比的检验方法识别残差序列中粗大

异常风速值检测；组合预测模型；残差分析；Bayesian后验比

风电场运行数据中的风速值是分析监测风机运行状态和预测风机出力情况的重要依据。因传感器故障和传输信道噪声产生的异常叠加在监控终端的数据中，由于风速特有的间歇性和不确定性[1]，造成异常值在风速序列特征信息不明显，使得异常值辨识困难。

在诸多风速功率预测方法中，如人工神经网络[2-4]、支持向量机[5]、卡尔曼滤波[6]和时间序列分析法[7-8]都直接采用测量数据进行分析计算，对含有异常值的数据建模分析势必会影响预测精度。因此，分析数据前需要对异常数据识别与修正。在异常数据检测方面，文献[9]最早提出了运用统计学的思想检测异常值，根据历史数据设定一个概率模型，如果数据服从同一分布则判定为正常值，反之则为异常数据点，该方法的统计量计算复杂且统计参数对辨识异常值异常敏感。文献[10]是基于距离的方法检测异常值，需要计算每个点之间的距离，通过相似度检测异常距离，因计算量过大，不适处理大量的风速时间序列。文献[11]提出了小波模极大值的方法辨识异常风速值，该方法通过采用阈值和Lipschitz指数联合判定异常风速值，由于小波方法不能兼顾时间分辨率和频率分辨率，易产生漏检现象。文献[12]提出了采用Gibbs抽样算法估计Bayesian参数并通过阈值检测异常值，该方法只适用于线性系统不适用于多变的风速序列。文献[13]提出了利用支持向量机的回归估计值与实测值之间的残差来识别测量数据中的异常数，由于拟合残差的方差异常敏感，方差值决定着辨识粗大误差的准确性。

基于以上分析，结合传统残差分析和Bayesian参数估计方法，本文提出了组合预测模型和边缘化后验比的方法检测异常风速值。首先分别建立Adaboost-BP网络和EMD-LS-SVM的单一预测模型，通过计算每个模型的方差确定组合预测模型的最优权重系数，使得到的残差序列更准确。为了降低Bayesian后验概率的未知参数的数目，对其参数边缘化处理可简化计算方法，并剔除后验比值小于检测阈值的异常风速值。最后采用ARIMA方法修正异常风速点，从而优化了风速数据的质量。通过对仿真数据异常点的检测结果验证了本文方法的可行性，并对甘肃酒泉风电场的实测运行风速序列进行异常检测和修正，预测结果表明对风速数据处理后可提高预测精度。

1 异常风速值检测算法

由于异常风速值在风速序列中表征不明显，用现有的异常检测方法不易检测出[14-17]，为了凸显异常风速值的特征信息，本文通过建立风速预测模型计算出预测值，比较预测值与测量值之间的差值，得到异常特征明显的残差序列。残差序列是由随机误差、系统误差和粗大误差构成，而系统误差受风速传感器测量精度和风速预测精度的影响，系统误差幅值波动稳定，误差的绝对值小于等于3σ[18]，且服从高斯分布。而粗大误差是由传感器故障和数据存储故障产生，具有随机性和幅值波动大的特点[19]，其误差绝对值大于3σ。针对这种特点，本文利用边缘化后验比的方法检测识别粗大误差点，从而间接地检测出风速序列的异常值。

1.1 预测模型的选取

常见的风速预测模型包括：持续法[20]、ARMA预测法、神经网络预测法和支持向量机预测法。由于风速的随机性和间歇性，造成单一预测模型精度不高，预测模型的系统误差较大，不利于准确识别残差序列中的粗大误差值。因此，本文选取基于自方差优选的组合预测方法提高预测精度，尽可能地使系统误差达到最小，尽可能地接近真实风速时间序列。

1.1.1 Adaboost-BP模型

在BP网络建立过程中存在过拟合、泛化能力弱和易陷入局部最优的问题，本文引入Adaboost迭代算法改进BP算法[21-22]，使其将训练集中不同的弱学习器结合起来搭建成一个稳健的强学习器。Adaboost迭代算法的基本思想是在训练过程中重视预测误差大的样本和性能好的弱学习器，从而提高了BP网络的泛化能力和预测精度。

建立Adaboost-BP模型的过程如下：

1）对训练集进行数据归一化处理，然后将数据分成N组，每组数据中含有n个训练值和m个预测数据。

2）随机选取一组数据，建立结构为3-6-1的BP网络，其中NN（tx）表示第t次构建的BP网络。在该网络下计算每组数据的预测误差εi和N组数据的平均

3）更新样本权重Dt其中βt=εt/的归一化因子，D0（i）=1/N。根据βt可得到弱学习器的权重为

4）重复步骤2）和3），直到迭代的次数T＞10或者预测平均误差εt＜10－5跳出循环。

5）最终得到强学习器的Adaboost-BP预测模型表达式为

1.1.2 EMD-LS-SVM模型

风速序列是一组随机性较强的非线性、非稳态的时间序列，单一的模型存在预测精度低、泛化能力弱的问题。经验模态分解[23]EMD常用于处理非线性、非稳态的信号，把信号分解成不同频率的序列，降低了信号中的不同频率之间的相互影响。针对不同频率的分解量固有模态函数（IMF）和趋势量（Res）分别建立LV-SVM回归模型[24-25]。最后对不同分量进行合成重构得到预测结果。

建立EMD-LS-SVM模型的步骤：

1）输入训练集数据，采用EMD方法对风速序列进行分解得到多个IMF分量和Res分量的代数和，即：

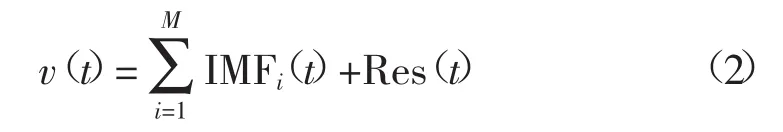
式中：M为IMF分量的个数；IMFi（t）为风速时间序列的第i个固有模态函数；Res（t）为分解后的趋势分量。

2）分别对分量IMFi（t）和Res（t）建立LV-SVM回归模型，构造的拉格朗日函数计算方法算法如下：

式中：c为容错惩罚系数，c＞0；ξi为松弛因子，ξi≥0；w为权向量；b为常数；αi（i=1，2，…，l）为拉格朗日乘子。本文参考文献[20]的方法确定超参数，选取c= 30，σ2=0.22。

通过式（4）计算出LS-SVM回归函数表示为

式中：高斯核函数K（x，xi）=e－‖x－xi‖2/（2σ2）。

3）利用式（4）建立各个分量的模型，并预测出每个分量的值，对分量结果进行合成重构，得到最终的预测值y2（x）。

1.1.3 建立风速组合预测模型

方差优选风速组合预测模型的风速输出y（t/ t－1）为

式中：λ1为在t时刻Adaboost-BP网络预测模型的权重值；λ2为在t时刻EMD-LS-SVM预测模型的权重值，且λ1+λ2=1。y（1t/t－1）为t时刻Adaboost-BP网络预测模型的预测值；y（2t/t－1）为t时刻EMD-LS-SVM预测模型的预测值。

求取最优权重的过程等同为如下优化问题：

采用构造拉格朗日函数的方法求解式（7），可以解得：

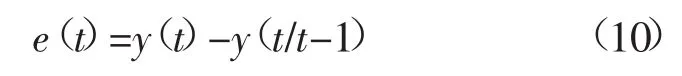
通过式（10）得到的残差序列是由预测模型产生的系统误差（误差较小接近于0）和异常风速值产生的粗大误差的代数和构成。随后通过识别粗大误差来确定风速值的异常情况。

1.2 Bayesian后验比检测准则

由于残差序列服从高斯分布[26]，因此根据Bayesian后验的思想，ALARCON-AQUINO V[27]等人建立检测窗口和学习窗口，其中学习窗口中的数据用于建立高斯分布，检测窗口中的数据用于检测该数据的异常情况。通过分析2个窗口的残差序列是否服从同一高斯分布的方法检测异常数据。如果检测窗口服从学习窗口的高斯分布，判为正常（系统误差）数据，反之，则判为异常（粗大误差）数据。

随着检测数据的不断增加，学习窗口中堆积了大量数据使得统计分析复杂。本文结合风速残差序列中粗大误差的分布特点，通过固定学习窗口中数据的长度L保持不变，并保持检测窗口只含有一个待检测的数据，利用学习窗口和检测窗口同步滑动实现残差序列中粗大误差的检测与识别。

根据学习窗口中L个数据的分布情况得到高斯分布N（0，δ2），读取检测窗口t时刻的残差值et。当et服从N（0，δ2）时，则et判为系统误差数据（正常风速点）；当et不服从N（0，δ2）时，则et判为粗大误差数据（异常风速点）。从粗大误差数据得到2个假设，分别为H0：t时刻的残差et为正常值；H1：t时刻的残差et为异常值。

在2个假设条件下，L+1个残差数据的似然分别为

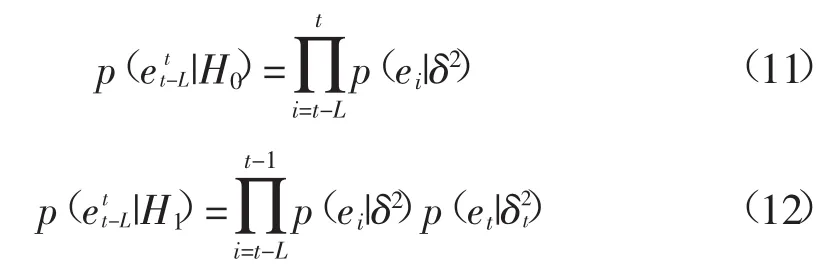
根据Bayesian原理[28]得到2个假设的后验概率分别为

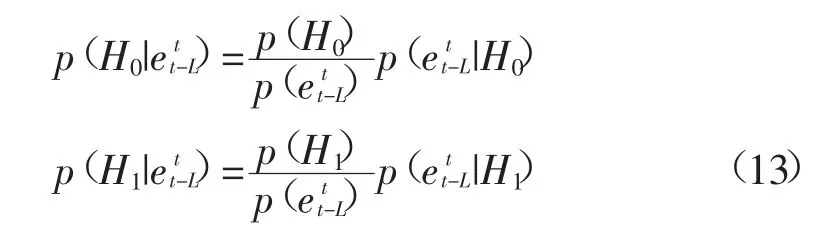
式中：假设H0和H1的先验概率分别为p（H0）和p（H1）；p（e）表示风速预测残差ei的先验概率i=t－L，…，t；后验概率p（H0|e）和p（H1|e）表示在取当前残差值e（ii=t－L，…，t）时，假设H0和H1成立的概率，可用统计量后验概率直接描述检测窗口残差值的异常情况。因此可以利用2个假设的后验概率的大小关系判断哪个假设成立，具体实施采用后验概率对数比作为异常判断准则：

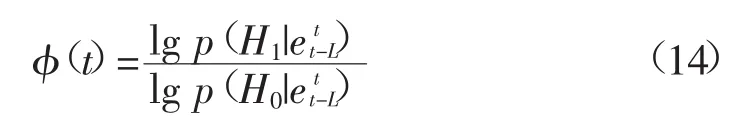
根据式（14）可知，如果et为粗大误差数据（v（t）为异常风速值），则异常假设的后验概率p（H1|远大于正常假设后验概率p（H0|e），即φ（t）小于η；如果et为系统误差（v（t）为正常风速值），则φ（t）大于η。本文选取检测阈值η=0.95，即异常值识别水平的可信度为0.95：

对于式（11）和式（12），如果计算假设H0和H1的似然函数，需要依据历史数据拟合概率密度函数求取高斯分布的方差δ2和δ，由于受到拟合精度的影响，计算出的方差精度不高，方差值的准确性直接关乎到检测异常值的合理性。为了避免因方差估计不准确造成的检测异常值不理想，本文引入边缘化处理的方法[29]，对方差δ2和用积分运算的方式估计出式（11）和式（12）的后验概率。所以式（13）可换成以下2个公式：

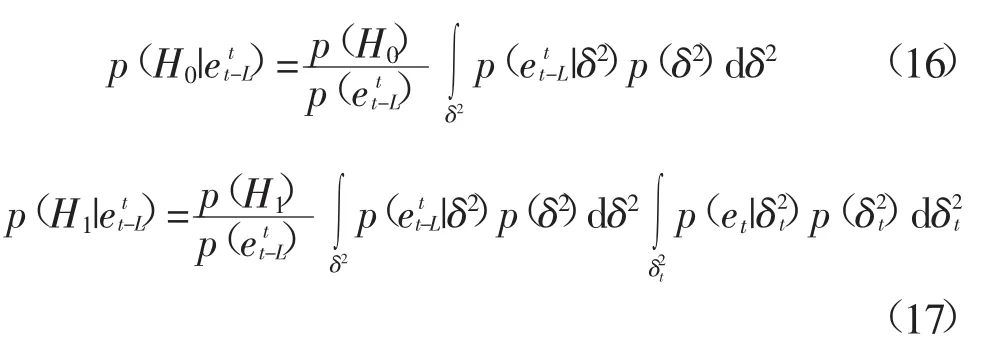
对式（13）采用边缘化处理后，式（16）和式（17）出现了2个未知分布即方差的先验密度p（δ2）和p（），引入Jeffreys提出的先验分布函数来计算p（δ）2和p（），根据文献[30]给出了在高斯分布条件下的先验计算方法p（t）=1/t，0＜t＜∞，将Jeffreys先验代入假设H0的式（16）可得：

式（18）中的被积函数正好为逆Wishart分布的密度函数，即。文献[28]给出了积分项逆Wishart分布的证明过程。因此式（18）化简为

同理对式（17）采用同样的推导过程可得出：

推导出的式（19）和式（20）可直接用于计算假设H0和H1的后验概率，再根据异常值判断准则式（14）计算出φ（t），通过比较φ（t）和η的大小进行检测残差序列中的粗大误差点。

2 异常风速值的修正

利用边缘化后验比的检测方法辨识拟合残差序列中的t时刻的粗大误差点，同时对该时刻的异常风速值剔除。为了进一步提高风速序列的连续性和可利用性，需要分两步对数据处理。第一步对异常风速序列二阶差分处理使其平稳化，第二步采用ARMA模型修正异常值。ARIMA算法[31-32]是依据风速序列的时序性和自相关性建立的，对异常风速值修正精度高。其中ARMA模型可以表示为

式中：α1，α2，…，αp为AR模型系数；β1，β2，…，βq为MA模型系数；εi为独立同分布的随机变量序列。

由于风速序列是非平稳序列，需要对其进行二阶差分平稳化，平稳化后的风速序列采用式（21）的方法建立ARMA模型，修正被剔除异常风速值。

3 检测异常风速值的步骤

本文通过组合预测方法与边缘化后验比方法相结合建立了风电场异常风速检测算法，对采集到的运行风速值优化处理，从而提高数据分析的精度。检测并修正风电场运行风速值的流程如图1所示，具体步骤如下所述。

图1 异常风速值检测流程Fig.1 Flow chart of anomaly w ind speed detection algorithm

1）输入待检测的风电场运行风速数据（含有异常风速值）。

2）建立单一预测模型。运用运行风速数据分别建立Adaboost-BP网络预测模型和EMD-LS-SVM预测模型，并计算出每个单一预测模型的预测误差e1和e2。

3）建立组合预测模型。采用拉格朗日的方法求取组合预测模型的最优权重系数λ1和λ2，得到组合模型的预测值y（t/t－1），并计算出含有粗大误差信息的残差序列e（t）。

4）计算后验比φ（t）。针对学习窗口中L个残差序列得到残差分布，并计算出检测窗口的残差值et服从2个假设H0和H1的后验概率，利用式（14）计算出后验比φ（t）。

5）判定异常风速值。比较后验比φ（t）与检测阈值η，当t时刻的后验比φ（t）小于η时，t时刻的残差为粗大误差，即t时刻的风速值异常；反之则为正常值。判定后同时滑动学习窗口和检测窗口，重复步骤4），检测t+1时刻的异常情况，直至检测完成。

6）修正异常风速值。采用ARIMA修正模型对步骤5）检测出的异常数据点进行修正，从而得到正常的风速值。

4 案例分析

4.1 案例一

为了验证本文所提出的组合预测和边缘化后验比算法识别异常值的有效性，采用本文所提方法检测余弦信号中的异常值，选取长度3 000的余弦信号，为了进一步验证检测算法的可靠性，在余弦信号再加入信噪比为10 dB的高斯噪声。前2 000个数据用组合预测模型的建立，后1 000个数据中随机加入10个异常点。用于异常检测的余弦信号如图2所示。

图2 含有异常值的仿真信号Fig.2 Simulation signalw ith abnormal value

用前2 000个数据点得到的组合预测模型对后1 000个数据进行预测，得到的残差序列如图3所示。从图3中可以看出，由预测系统造成的系统误差接近0，在残差序列中10个异常值以粗大误差的形式全部显示出。

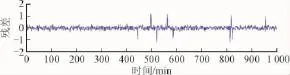
图3 仿真信号的残差序列Fig.3 Residual series of simulation signal

分别建立学习窗口和检测窗口，其中学习窗口的长度L为100，检测窗口为1，取p（H0）=0.95[14]。采用式（14）计算后验概率比。从图4中可以看出，残差序列中的粗大误差点的后验对数比值φ（t）显然远远小于其他时刻的比值。当φ（t）小于η时，判为异常点；否则残差序列正常。采用组合预测模型和后验概率比的方法全部检测出10个异常点的位置，证明了本文所提方法的可行性。

图4 仿真信号数据的检测结果Fig.4 Detection result of simulation signal

4.2 案例二

对甘肃酒泉风电场实际采集的数据进行异常风速检测，选取2010年5月15日—5月22日中的7 000个风速数据，其中将含有异常值的4 000个数据用于单一和组合模型的搭建，3 000个风速数据用于预测并得到残差序列。

从图6可以看出粗大误差点在600～1 000和2 100～2 400之间出现的频率比较高，而在图5中该段异常风速点很难被观察识别。组合预测的方法能有效地凸显异常风速点，为下一步的准确检测异常值提供了保障。

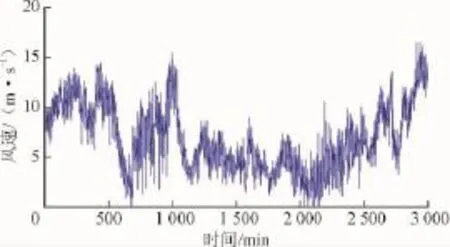
图5 酒泉风电场实测风速序列Fig.5 M easured w ind speed series from Jiuquan w ind farm s

图6 酒泉风电场的风速残差序列Fig.6 Residual series ofwind speed from Jiuquan wind farms

对残差序列采用学习窗口和检测窗口滑动的方式检测粗大误差点，固定学习窗口的长度L=100，统计学习窗口内的误差分布参数，并借助后验概率的方法在2个假设H0和H1的条件下计算出学习窗口t时刻的后验对数比。对比图6和7，发现残差序列中的较大粗大误差对应的后验对数比值明显小于检测阈值η。

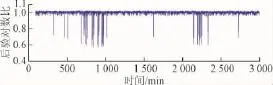
图7 酒泉风速数据的检测结果Fig.7 Detection result of w ind speed from Jiuquan w ind farm s

采用ARIMA方法修正粗大误差点所对应的异常风速值，使其得到正常的风速序列，为进一步的分析应用提供可靠的数据质量。

为验证本文识别剔除异常风速值的有效性，采用（RBF）神经网络预测算法[15-16]对修正后的2 900个风速序列进行预测。其中选取2 000个数据用于RBF模型的训练，900个数据用于预测结果的测试。选用平均绝对误差（MAE）、平均绝对百分误差（MAPE）、均方根误差（RMSE）作为预测结果评价指标。

从表1中的RBF预测结果发现，修正后的风速序列与含有异常值的风速序列相比，3项预测指标都有不同程度的提升，因此采用修正异常值后的风速序列进行风速预测可提高预测精度，为风电场风速序列的研究提供了可靠保障。

表1 酒泉风电场预测误差分析Tab.1 Prediction error analysis from Jiuquan w ind farms

5 结语

由于风电场测量风速数据中存在一些异常风速值，不经预处理直接对其进行预测分析严重影响预测精度，本文提出了Adaboost-BP与EMD-LVSVM的组合预测和边缘化后验比的检测算法。为了避免残差序列中的系统误差与粗大误差的混叠现象，使系统误差降低到最低，本文将含有异常值的数据采用组合预测方法获得训练模型，并得到残差序列。由于残差序列中的系统误差服从高斯分布，因此选用后验概率对数比的方法辨识系统误差与粗大误差。为了提高估计参数的鲁棒性，对估计参数边缘化处理，从而提高了检测算法的可行性。仿真结果表明，本文方法能合理地检测风电场异常风速值，可为短期风速预测提供可靠的数据质量。本文方法局限性有以下2点：第一，误差的大小取决于所建立的预测模型的精度，在以后的研究中需进一步探索合理的预测方法以降低系统误差；第二，本文的后验比检测方法是建立在误差服从高斯分布的假设下，但异常数据很难用服从一种单一的分布，今后需探索适用范围更广泛的检测异常值的方法。

[1]王勃，冯双磊，刘纯.考虑预报风速与功率曲线因素的风电功率预测不确定性估计[J].电网技术，2014，38（2）: 463-468. WANG Bo，FENG Shuanglei，LIU Chun.Uncertainty estimation of wind power forecasting considering wind speed and power curve factor[J].Power Grid Technology，2014，38（2）:463-468（in Chinese）.

[2]刘兴杰，岑添云，郑文书，等.基于模糊粗糙集与改进聚类的神经网络风速预测[J].中国电机工程学报，2014，34（19）:3162-3169. LIUXingjie，CEN Tianyun，ZHENGWenshu，etal.Neural network wind speed forecasting based on fuzzy rough set and improved clustering[J].Journal of Chinese Electrical Engineering Science，2014，34（19）:3162-3169（in Chinese）.

[3]艾格林，孙永辉，卫志农.基于MEA_Elman神经网络的光伏发电功率短期预测[J].电网与清洁能源，2016，32（4）:119-124. AIGelin，SUN Yonghui，WEIZhinong.Short-term photovolataic power forecasting based on MEA and elman neural network[J].Power System and Clean Energy，2016，32（4）:119-124（in Chinese）.

[4]于群，朴在林，胡博.基于EEMD和BP神经网络的短期光伏功率预测模型[J].电网与清洁能源，2016，32（7）: 132-137. YU Qun，PIAO Zailin，HU Bo.A hybridmodel for shortterm photovoltaic power forecasting based on EEMD-BP combined method[J].Power System and Clean Energy，2016，32（7）:132-137（in Chinese）.

[5]陈伟，郭建鹏，裴喜平，等.风电场短期风速变化区间与变化趋势预测算法[J].电力系统及其自动化学报，2015，27（9）:47-52. CHENWei，GUO Jianpeng，PEIXiping，et al.Short term wind speed variation range and variation trend prediction algorithm for wind farm[J].Proceedings of the CSU-EPSA，2015，27（9）:47-52（in Chinese）.

[6]修春波，任晓，李艳晴，等.基于卡尔曼滤波的风速序列短期预测方法[J].电工技术学报，2014，29（2）:253-259. XIU Chunbo，REN Xiao，LI Yanqing，et al.Short term forecasting method of wind speed series based on calman filter[J].Transactions of China Electrotechnical Society，2014，29（2）:253-259（in Chinese）.

[7]陈道君，李幕，杨楠，等.基于最优权系数的风电功率组合预测方法[J].电网与清洁能源，2016，32（4）:99-105. CHEN Daojun，LIMu，YANG Nan，et al.Combination forecastingmethod of wind power based on optimal weight coefficient[J].Power System and Clean Energy，2016，32（4）:99-105（in Chinese）.

[8]田波，朴在林，王慧.基于时间序列建模在风力发电功率短期预测中的研究[J].电网与清洁能源，2016，32（3）:115-119. TIAN Bo，PIAO Zailin，WANG Hui.Short term prodiction of wind power based on time series modeling[J].Power System and Clean Energy，2016，32（3）:115-119（in Chinese）.

[9]BARNET V，LEWIS T.Outlier in statistical data[M]. Chichester:John Wiley and Sons，1994.

[10]ZHENG Le，MIN Yong.Raw wind data preprocessing:A data-mining approach[J].IEEE Transactions on Sustainable Energy，2015，6（1）:11-19.

[11]李丽，叶林.风速数据奇异点辨识研究[J].电力系统保护与控制，2011，39（21）:92-97. LILi，YE Lin.Research on singular point identification of wind speed data[J].Power System Protection and Control，2011，39（21）:92-97（in Chinese）.

[12]尚华，冯牧，张贝贝.基于Bayesian方法的参数估计和异常值检测[J].重庆邮电大学学报（自然科学版），2016，28（1）:138-142. SHANG Hua，FENG Mu，ZHANG Beibei.Parameter estimation and outlier detection based on bayesian method[J].Journal of Chongqing University of Posts and Telecommunications，2016，28（1）：138-142（in Chinese）.

[13]王雷，张瑞青，盛伟，等.基于支持向量机的回归预测和异常数据检测[J].中国电机工程学报，2009，29（8）: 92-96. WANG Lei，ZHANG Ruiqing，SHENG Wei，et al. Regression prediction and anomaly data detection based on support vector machine[J].Proceedings of the CSEE，2009，29（8）:92-96（in Chinese）.

[14]张锋利，陈文献，贾海英.支持向量机和BP神经网络在水轮发电机轴承故障诊断中的应用[J].电网与清洁能源，2013，29（4）:62-66. ZHANG Fengli，CHENWenxian，JIA Haiying.Application of support vectormachines and BP neural network in the rolling bearing of hydraulic turbine generator fault diagnosis[J].Power System and Clean Energy，2013，29（4）:62-66（in Chinese）.

[15]张宇航，兰生.基于广义神经网络与模糊聚类的变压器故障诊断[J].高压电器，2016，52（5）:116-120. ZHANG Yuhang，LAN Sheng.Transformer fault diagnosis based on GRNN and FCM[J].High Voltage Apparatus，2016，52（5）:116-120（in Chinese）.

[16]苗长新，申坤，钟世华，等.基于优化神经网络和DGA的变压器故障诊断[J].高压电器，2016，52（11）:163-167. MIAO Changxin，SHEN Kun，ZHONG Shihua，et al. Power transformer fault diagnosis based on improved neutral network and DGA[J].High Voltage Apparatus，2016，52（11）:163-167（in Chinese）.

[17]刘太洪，赵永雷.动态加权模糊聚类在变压器故障诊断中的应用研究[J].电网与清洁能源，2016，32（4）:89-92. LIU Taihong，ZHAO Yonglei.Application of dynamic weighted fuzzy clustering algorithm to fault diagnosis of transformer[J].Power System and Clean Energy，2016，32（4）:89-92（in Chinese）.

[18]刘辉舟，周开乐，胡小建.基于模糊负荷聚类的不良负荷数据辨识与修正[J].中国电力，2013，46（10）:29-34. LIU Huizhou，ZHOU Kaile，HU Xiaojian.Identification and correction of bad load data based on fuzzy load clustering[J].Electric Power，2013，46（10）:29-34（in Chinese）.

[19]BRETASN G，BRETAS A S，PIERETIS A.Innovation concept for measurement gross error detection and identification in power system state estimation[J].IETGeneration，Transmission&Distribution，2011，5（6）:603-608.

[20]李丽，叶林.基于改进持续法的短期风电功率预测[J].农业工程学报，2010，26（12）:182-187. LILi，YE Lin.Short term wind power prediction based on improved continuation method[J].Transactions of the Chinese Society of Agricultural Engineering，2010，26（12）:182-187（in Chinese）.

[21]刘亚南，范立新，徐钢，等.基于非负矩阵分解与改进极端学习机的变压器油中溶解气体浓度预测模型[J].高压电器，2016，52（1）:162-169. LIU Yanan，FAN Lixin，XU Gang，et al.Concentration prediction model of dissolved gases in transformer oil based on NMF and improved ELM[J].High Voltage Apparatus，2016，52（1）:162-169（in Chinese）.

[22]柳玉，郭虎全.基于AdaBoost与BP神经网络的风速预测研究[J].电网与清洁能源，2012，28（2）:80-83. LIU Yu，GUO Huquan.Wind speed prediction based on AdaBoost and BP neural networks[J].Power System and Clean Energy，2012，28（2）:80-83（in Chinese）.

[23]吕帅，张靠社.基于小波变换去噪预处理的EMD谐波检测方法[J].电网与清洁能源，2016，32（6）:59-61. LÜ Shuai，ZHANG Kaoshe.EMD harmonic detection method of denoising preprocessing based on wavelet transform[J].Power System and Clean Energy，2016，32（6）:59-61（in Chinese）.

[24]郑港，鄢小虎，谢齐家，等.一种基于萤火虫支持向量机的油色谱在线数据校正方法[J].高压电器，2013，49（9）:23-27. ZHENGGang，YAN Xiaohu，XIEQijia，etal.Method for the oil chromatographic on-line data reconciliation based on GSO and SVM[J].High Voltage Apparatus，2013，49（9）:23-27（in Chinese）.

[25]曾杰，张华.基于最小二乘支持向量机的风速预测模型[J].电网技术，2009，33（18）:144-147. ZENG Jie，ZHANG Hua.Wind speed forecasting model based on least square support vector machine[J].Power System Technology，2009，33（18）:144-147（in Chinese）.

[26]叶林，任成，赵永宁，等.超短期风电功率预测误差数值特性分层分析方法[J].中国电机工程报，2016，36（3）:692-700. YE Lin，REN Cheng，ZHAO Yongning，etal.Super short term wind power prediction error numerical characteristic analysismethod[J].Journal of Chinese Electrical Engineering Science，2016，36（3）:692-700（in Chinese）.

[27]ALARCON-AQUINO V，BARRIA JA.Anomaly detection in communications[J].IET Journals&Magaines，2001，148（6）:355-362.

[28]GUSTAFSSON F.The marginalized likelihood ratio test for detecting abrupt changes[J].IEEE Transactions on Automatic Control，1996，41（1）:355-362.

[29]苏卫星，朱云龙，胡琨元，等.基于模型的过程工业时间序列异常值检测方法[J].仪器仪表报，2012（9）:2080-2087. SUWeixing，ZHU Yunlong，HU Kunyuan，et al.Method for detecting outliers in process industry time series based on model[J].Instrument and Meter，2012（9）：2080-2087（in Chinese）.

[30]BERNARDO JM，SMITH A F M.Bayesian theory[M].

New York:Wiley，1994.

[31]GONG Shuhong，GAO Yifeng，SHI Houbao，et al.A practical MGA-ARIMA model for forecasting real-time dynamic rain-induced attenuation[J].IEEE Transactions on Radio Science，2013，48（3）:208-225.

[32]YUNUS K，THIRINGER T，CHEN Peiyuan.ARIMA-based frequency-decomposedmodeling ofwind speed time series[J].IEEE Transactions on Power Systems，2016，31（4）:2546-2556.

Anomaly W ind Speed Detection M ethod w ith Im proved Bayesian Posterior Ratio

CHENWei，WU Butuo，PEIXiping，WANG Yizhe
（Institute of Electrical Engineering and Information Engineering，Lanzhou University of Technology，Lanzhou 730050，Gansu，China）

As wind speed data contains abnormal values from wind farms，in order to optimize the quality ofwind power data，this paper proposes an outlier detection method with the improved Bayesian posterior ratio.To reduce the prediction error，the paper establishes a combination forecasting model based on BP network and least square support vectormachine. The residual error sequence is obtained by calculating the deviation between the predicted value and themeasured value. The gross errors in the residual series are identified by the test method of Bayesian posterior ratio，and this approach can improve the reliability and determine the location of the abnormal value.Finally，we use the ARIMA method to correct the abnormal wind speed.RBF prediction results show that the proposed method can accurately identify outliers，thus improving the forecasting accuracy ofwind speed.

anomaly wind speed detection method；combined forecasting model；residual analysis；Bayesian posterior ratio

2016-08-15。

陈 伟（1976—），男，博士，教授，博导，主要研究方向为电能质量分析和控制、新能源发电技术；

（编辑 冯露）

国家重点研发计划（2016YFB0601600）；国家自然科学基金项目（51267012）；甘肃省科技支撑工业计划项目（1504GKCA033）。

Project Supported by National Key Research and Development Program（2016YFB060 1600）；the National Natural Science Foundation of China（51267012）；Science and Technology Support Industry Program of Gansu Province（1504GKCA033）.

1674-3814（2017）02-0104-08

TM614

A

误差，从而确定异常风速值的位置，并利用ARIMA方法修正异常风速值。RBF预测结果表明，所提方法能准确识别异常值，从而提高了风电场短期风速预测精度。

吴布托（1988—），男，硕士研究生，主要研究方向为新能源发电技术。