电动汽车峰谷分时充放电价同步优化模型研究

孙波，王振兴，孙佳佳

（上海电力学院经济与管理学院，上海 200090）

电动汽车峰谷分时充放电价同步优化模型研究

孙波，王振兴，孙佳佳

（上海电力学院经济与管理学院，上海 200090）

电动汽车在无引导机制下入网会导致负荷随机性变化，增加系统控制难度。通过制定电动汽车峰谷分时充放电价能够引导电动汽车用户分时段入网参与充放电，进而有利于系统负荷的削峰填谷。首先，通过蒙特卡罗模拟法建立单台电动汽车无序模式下充放电功率模型，并分析规模化入网对系统负荷的影响；然后，构建电动汽车充放电价同步优化模型，建立电动汽车充放电电量与充放电价的联系，实现充放电价的同步优化；最后，利用粒子群优化算法对模型进行求解。算例表明，通过制定电动汽车峰谷分时充放电价同步优化策略能够达到系统负荷削峰填谷的目的，同时能够增加电动汽车用户的收益。

削峰填谷；充放电价；同步优化；蒙特卡洛模拟；粒子群

随着能源紧缺与碳排放日益加剧以及电池技术的发展[1-2]，电动汽车（electric vehicle，EV）作为新能源汽车，在国家大力推广下日益普及[3]。而大量EV入网，会影响到电网的安全与稳定运行[4]，如增加电网控制难度，影响电能质量等[5]。车电互联（Vehicle to Grid，V2G）技术是电能的双向互动技术，EV通过V2G技术入网，既能从电网中充电，又能将多余电能反馈回电网，起到对电网调峰、调频等的作用[6]。因此，通过引导EV用户参与V2G，能够达到使系统负荷削峰填谷的目的，提高EV入网下系统的安全与稳定性[7]。

EV入网参与V2G受多方面因素影响，其中，充放电电价作为最主要的可控制因素，是引导EV用户参与V2G的关键[8]。在统一的充放电价模式下，由于缺少电价引导机制，用户参与V2G具有较强的随机性，不利于系统的安全与稳定运行。通过制定峰谷分时充放电价，能够引导EV用户在负荷低谷时段充电，高峰时段放电，在减少用户充电成本、增加放电收益的同时，优化EV入网后负荷[9]。在EV峰谷分时充放电价的研究中，文献[10]在分析EV充放电成本和收益的基础上，基于需求理论及EV充放电特性，建立以负荷波动最小为目标的峰谷分时充放电价模型；文献[11]基于用户对电价反应曲线及电量电价弹性矩阵，构建了以平滑系统负荷和最大化用户收益为目标的峰谷分时充放电价模型，通过算例验证了峰谷分时充放电电价策略对平滑系统负荷及最大化用户收益的可行性；文献[12]在兼顾电网利益和车主满意度的基础上，建立用户对电价变化的响应度模型，设计了最优峰谷分时充放电价方案。以上文献都是在优化系统负荷的基础上构建峰谷分时充放电价模型，但均未分析峰谷分时充电电价与放电电价之间的相互关系，以及2种电价之间的相互影响。

本文从研究峰谷分时充放电价的相互关系及电价与电量的相互响应出发，首先构建了无序模式下EV充放电期望功率概率模型，利用蒙特卡罗算法模拟单台EV在一天内的充放电功率曲线，分析EV规模化入网对负荷的影响，然后以EV入网下的负荷波动最小为目标函数，建立峰谷分时充放电价同步优化模型，最后采用粒子群优化算法对模型进行求解。算例结果显示，通过对峰谷分时充放电价的同步优化，其系统负荷较无序模式下更为平滑，且用户充放电收益较无序模式有较大程度提高。

1 无序模式下EV充放电功率模型

1.1 充电功率模型

在无序模式下，EV起始充电时刻服从正态分布，其概率密度函数为[13]

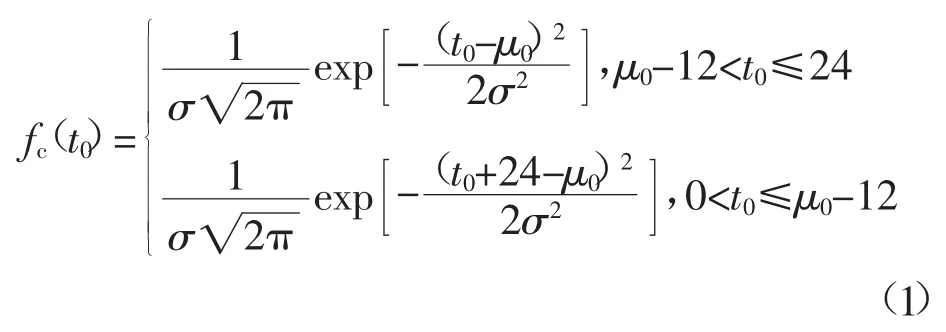
其中，μ0=17.6，σ=3.4，t0为起始充电时刻。

其概率密度曲线如图1所示。

定义Q为EV电池容量，最大放电深度为D，充电功率为Pc，则有其最大充电时长

令δtsc=0表示在某一充电时刻tsc，EV处于非充电状态；δtsc=1表示在tsc时刻处于充电状态，起始充电时刻为t0。EV在tsc时刻处于非充电和充电状态的概率分别为

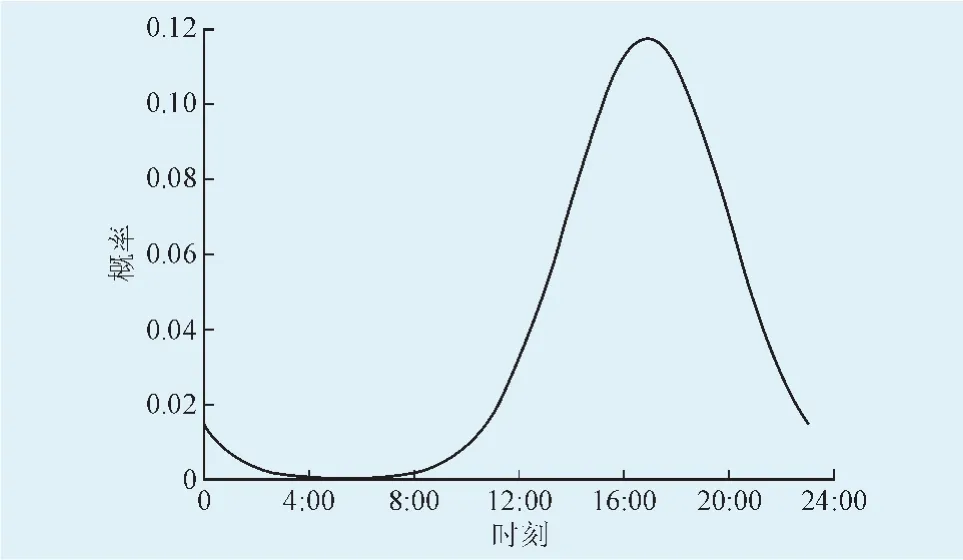
图1 EV起始充电时刻概率密度曲线Fig.1 Probability density curve of the initial charge time

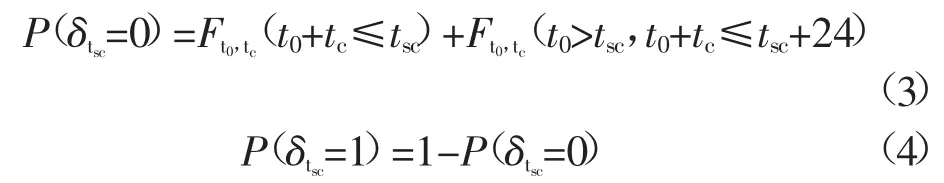
式中：Ft0，tc为起始充电时刻和充电时长的联合密度分布函数。则在tsc时刻，单台EV期望充电功率Pc，tsc= P（δtsc=1）Pc。

1.2 放电功率模型EV日行驶里程满足对数分布[14]

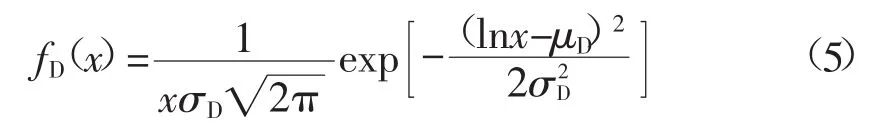
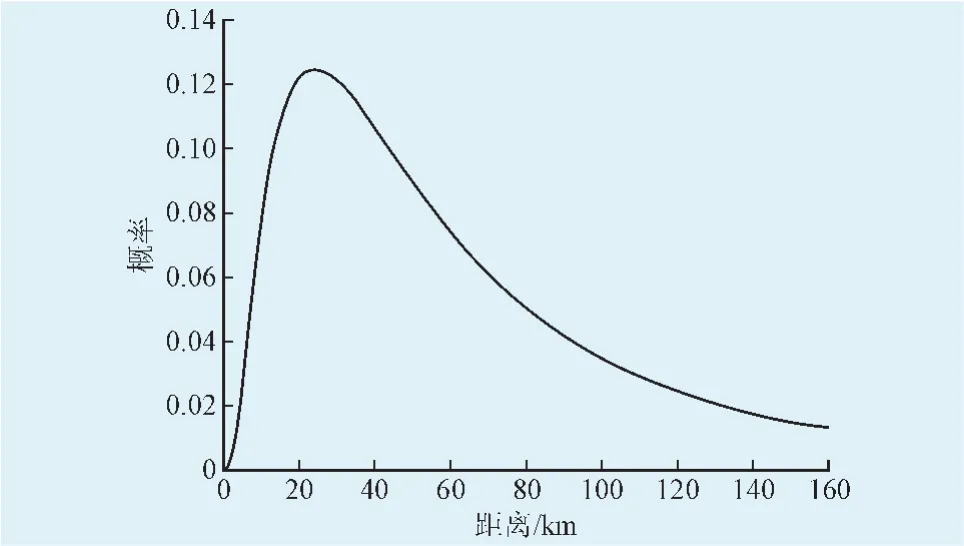
图2 日行驶里程概率密度曲线Fig.2 Probability density curve of daily travelm ilage

其中，uD=3.2，σD=0.88。EV日行驶里程概率密度曲线如图2所示。EV行驶消耗电量，x为行驶里程，E为EV能效，单位为km/kW·h。于是有EV可放电时长td=，Pd为EV放电功率。

假设EV在放电时段Td内服从均匀分布，则其概率密度为

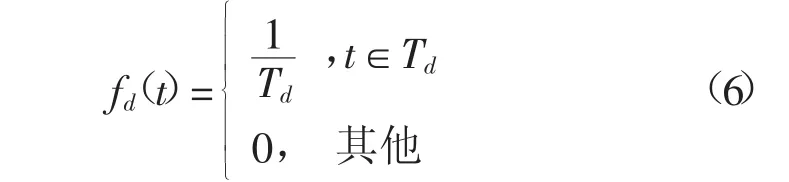
令δtsd=0表示在某一放电时刻tsd，EV处于非放电状态；δtsd=1表示在tsd时刻处于放电状态，起始放电时刻为t1。在tsd时刻处于非放电与放电状态的概率分别为

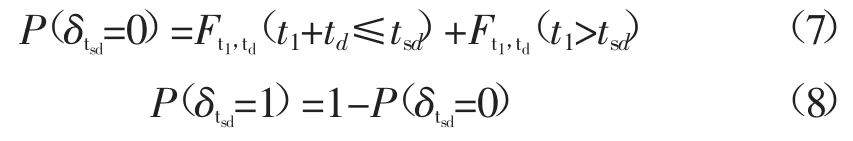
式中：Ft1，td为起始放电时刻和放电时长的联合密度分布函数。则在tsd时刻，单台EV期望放电功率Pd，tsd= P（δtsd=1）Pd。

给定EV电池容量Q=40 kW·h，放电深度D=0.85，EV能效E=5 km/kW·h[15]，充放电功率Pc=Pd=5 kW/h，Td∈［0，24］。结合式（1）～式（8），取每个时刻样本空间为10 000，利用蒙特卡罗方法模拟无序模式下单台EV充放电功率曲线，如图3所示。

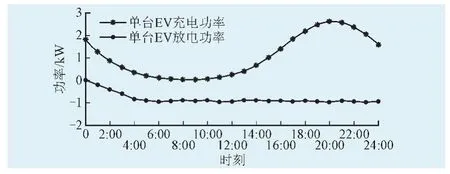
图3 无序模式下单台EV充放电功率曲线Fig.3 Power curve of charge and discharge of a single EV in disordermode

1.3 EV规模化入网对负荷的影响

图4为无EV参与下的负荷曲线和无序模式下不同数量EV参与V2G的负荷曲线。由上图可知，EV在无序模式下入网，会导致谷时段负荷较原系统负荷进一步降低，峰时段负荷进一步上升，且EV入网数量越多，峰谷差越大，严重影响电网的安全与稳定运行。因此，需要制定峰谷分时充放电价，引导EV用户分时段充放电，实现对系统负荷的削峰填谷。

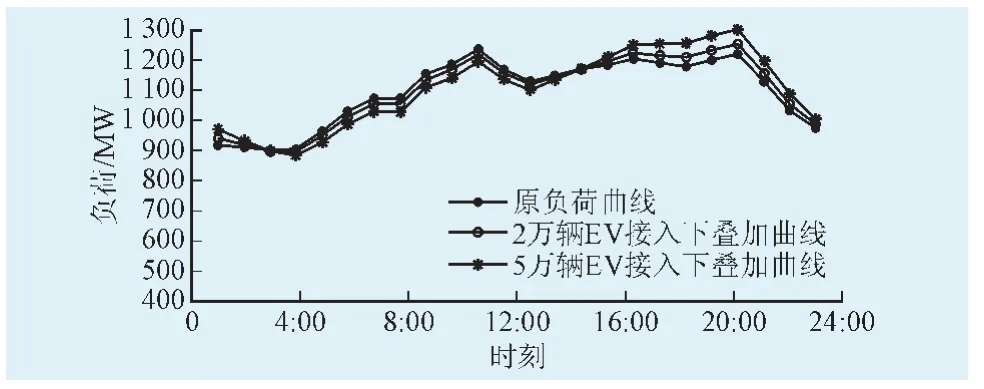
图4 不同数量EV接入下的负荷曲线Fig.4 Load curvesw ith different quantities of EVs accessing the power grid

2 峰谷分时充放电价同步优化模型

电量电价响应度模型是实现充放电电价与相应充放电电量相互关联的模型，即在电价引导机制下，某一时段充放电价的改变会引导用户选择是否在相应时段参与充放电，进而影响到系统负荷的变化。本文通过建立降低峰谷差，平滑系统负荷的优化模型，调节不同时段EV入网下的充放电量，由电量电价响应度模型实现充电电价与放电电价的同步优化。

2.1 电量电价响应度模型

用户对电价的响应体现在分时段改变用电方式，以减少用电支出。通过引用电量电价弹性矩阵，可达到量化用户响应的目的[16]。电价弹性即为用电量变化率与电价变化率之比。其弹性价格响应度模型如式（9）所示[17]。

式中：Q′i为实行峰谷电价后i时段的用电量；Qi为实施前i时段用电量；C、ΔCi分别为实施前电价与实施峰谷电价前后电价的变化量；E为弹性矩阵。

设EV充电实施峰谷电价后，其峰平谷时段充电电价分别为Ccf、Ccp、Ccg，实施前为统一充电电价Cc，于是有

式中：Qcf、Qcp、Qcg分别为实施峰谷充电电价后，峰、平、谷时段对应的EV充电电量；Qc1、Qc2、Qc3为实施峰谷电价前，对应时段的EV充电电量；ΔCc1、ΔCc2、ΔCc3为峰谷电价实施前后电价变化量；Ec为充电电价弹性矩阵。

设EV实施峰谷电价后，其峰平谷时段放电电价分别Cdf、Cdp、Cdg，实施前放电电价为Cd，于是有

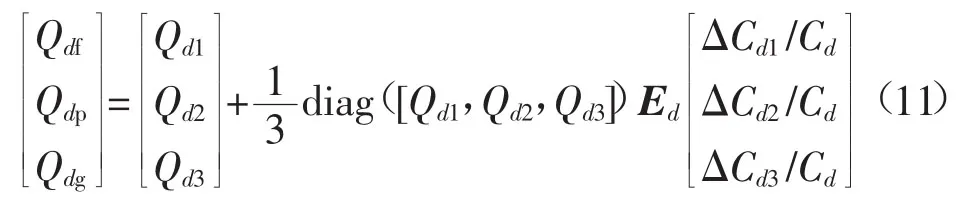
式中：Qdf、Qdp、Qdg分别为实施峰谷放电电价后，峰、平、谷时段EV对应的放电电量；Qd1、Qd2、Qd3为实施峰谷电价前，EV对应时段放电电量；ΔCd1、ΔCd2、ΔCd3为峰谷电价实施前后电价变化量；Ed为放电电价弹性矩阵。

2.2 基于削峰填谷的负荷优化模型

本文从降低系统负荷峰谷差，平滑系统负荷的角度优化EV用户不同时段的充放电电量，构建模型。取i时段处于充电状态的EV数量为nc，i，处于放电状态的EV数量为nd，i，则有i时段EV总充电功率Pc，i= nc，iPc，总放电功率Pd，i=nd，iPd。EV入网参与V2G，要达到削峰填谷的目的，可建立目标函数

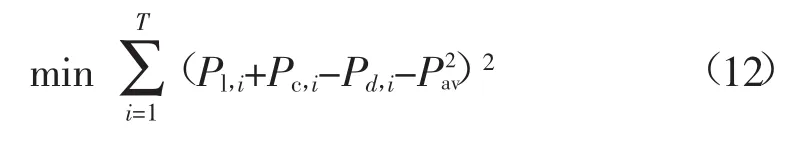
式中：Pl，i为系统常规负荷；Pav为EV接入后的平均负荷，可表示为

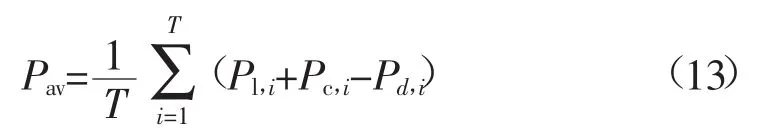
结合EV接入后的总充放电功率，可计算不同时段下的充放电电量。式（14）、式（15）分别为峰时段Tf下的充放电电量

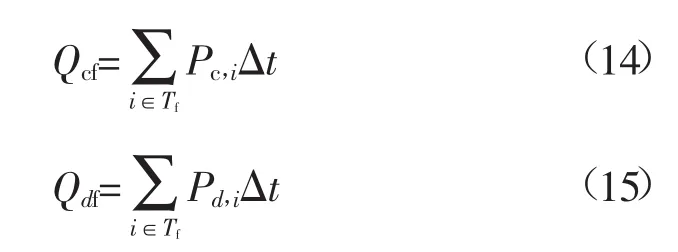
式中：Δt为i时段时长。同理，可计算出平时段Tp下的充放电电量Qcp、Qdp及谷时段Tg下的充放电电量Qcv、Qdv。

约束条件包括同一时段充放电EV数量的约束及总的充放电量的约束，如式（16）、式（17）。

3 粒子群算法

本文需要求解的基于削峰填谷的负荷优化模型为含约束条件的单目标非线性规划问题，采用粒子群优化算法对模型进行求解[18]。

粒子群算法为群智能随机优化算法，其算法步骤如下[19]：

1）初始化粒子位置和速度，设定种群规模为30，迭代次数为200。

2）根据每个时段内充放电EV数量，计算T时段内负荷曲线。

3）比较各负荷曲线峰谷差，并记录最优解，对比较后的各时段充放电EV数量进行更新。

4）将每个粒子的最小峰谷差与所有粒子最小峰谷差进行比较，用比较后每个粒子的最小峰谷差取代原所有粒子的峰谷差，同时保存粒子的当前状态。

按相应改进算法重新设定粒子，返回步骤2），直至完成设定的迭代次数或满足事先给定的精度要求为止。其算法流程如图5所示。

图5 粒子群算法流程图Fig.5 Flow diagram of the PSO

4 算例分析

表1为某电网典型日负荷，给定峰、平、谷时段分别为Tf=[9:00，22:00]、Tp=[7:00，8:00]∪[23:00，24:00]、Tg=[1:00，6:00]。

表1 典型日负荷Tab.1 Typical daily load of power grid

取峰谷电价实施前充电电价Cc=0.50元/kW·h，放电电价Cd=0.70元/kW·h。给定弹性矩阵

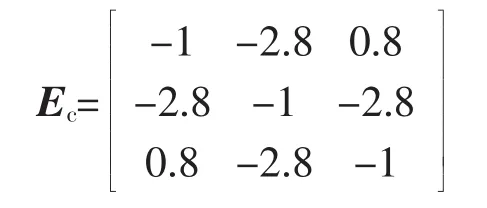
根据文中模型，利用粒子群算法可模拟出50 000辆EV入网参与V2G的负荷曲线，如图6所示。在系统负荷优化前，EV入网会使系统峰谷差变大，并出现新的最低谷负荷882.8 MW，和新的最高峰负荷1 302.8 MW，其峰谷差较原负荷增加了26%，严重影响了系统的经济性与安全性[20]，且由于随机性的充放电使相邻时段的负荷变化不平稳，势必会增加电网的优化控制与规划难度[21]。而通过优化后的负荷曲线，其谷时段负荷增加，峰时段负荷降低，峰谷差较原负荷减小了38.7%，且相邻时刻间负荷实现了平滑过渡，大大提高了系统的稳定性。

图6 EV入网下负荷曲线Fig.6 The load curve w ith EVs accessing the power grid

取Δt=1 h，结合式（14）、式（15），可计算出负荷优化前后EV入网下的峰平谷时段充放电电量及电量变化率，如表2所示。

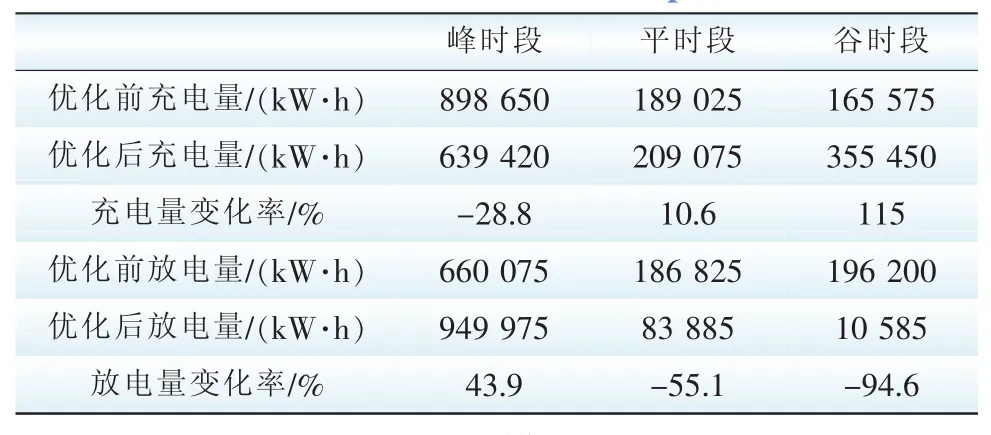
表2 负荷优化前后各时段电量及变化率Tab.2 Electric quantity and quantity rate at the different time before and after optim ization

由表2可知，通过对规模化入网的EV进行优化，对于EV充电，在平时段电量较优化前稍微增加的情况下，其充电电量较多地由峰时段转移至谷时段，且谷时段充电增量超出优化前一倍；对于EV放电，其平时段和谷时段放电量都明显降低，谷时段甚至降至优化前放电量的一半，而峰时段放电量较优化前增加了43.9%。结合式（10）、式（11），可得出负荷优化前后各时段及电价变化率，如表3所示。

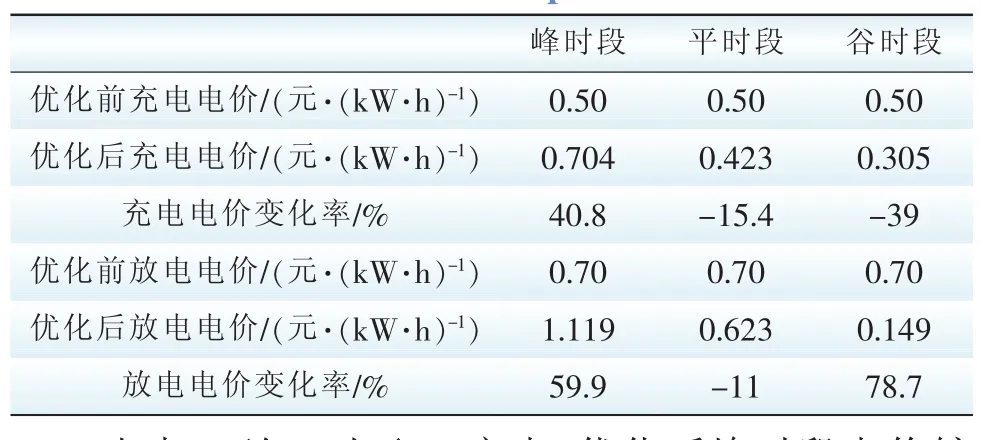
表3 负荷优化前后各时段充放电价及变化率Tab.3 Charge and discharge price and price rate before and after optim ization

由表3可知，对于EV充电，优化后峰时段电价较优化前显著增加，平时段和谷时段较优化前都有所降低，且谷时段较为显著；对于EV放电，峰时段电价较优化前明显增加，而平时段和谷时段都有所降低，且谷时段降低较为明显。

由表2和表3可知，通过制定峰谷分时充放电价同步优化策略，能够有效引导用户在不同时段进行充放电，使EV入网后系统负荷平滑过渡，实现削峰填谷。表4给出了50 000辆EV在一天内优化前后总充电费用及放电收益。

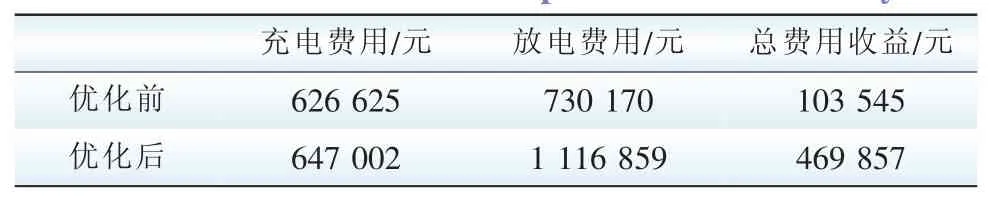
表4 优化前后EV用户在一天内充电总费用及放电总收益Tab.4 Total charging expense and discharge revenue of EV users before and after optim ization in one day

由表4可知，用户整体充电费用较优化前变化不大，增加了3.25%，放电费用较优化前增加了52.96%，明显高于充电费用增幅，且用户获得的总收益较优化前增加了353.8%，大大提高了用户的收益水平。在实施峰谷分时充放电价后，用户平均单日收益由2.07元增长为9.397元。因此，通过实施峰谷分时充放电价同步优化策略，既能实现使系统负荷削峰填谷的目的，又能增加用户收益，具有可行性。

5 结论

本文在已有文献研究的基础上，构建了峰谷分时充放电价同步优化模型，并采用粒子群算法对模型进行求解。通过算例，可得出以下结论。

1）EV在无价格引导机制下入网会导致负荷波动随机性，增加系统控制难度。采用峰谷分时充放电价同步优化模型，能有效降低EV入网下的峰谷差，实现削峰填谷。

2）在只考虑用户充电费用及放电收益下，峰谷分时充放电价策略能够较大幅度提高用户总收益。

3）采用本文同步优化模型，能够实现充电电价与放电电价的同步优化，使不同数量EV入网能够对应不同的充放电价，引导并约束用户在不同时段进行充放电，进而优化系统负荷。

在智能电网背景下，风电作为清洁能源，与EV协同入网下的充放电电价将是今后研究的方向。

[1]刘俊杰，李树林，范浩杰，等.情景分析法应用于能源需求与碳排放预测[J].节能技术，2012，30（1）：70-75. LIU Junjie，LIShulin，FAN Haojie，et al.Energy demand and carbon emissions forecasting by themethod of scenario analysis[J].Energy Conservation Technology，2012，30（1）：70-75（in Chinese）.

[2] 刘洁，王菊香，邢志娜，等.燃料电池研究进展及发展探析[J].节能技术，2010，28（4）：1-5. LIU Jie，WANG Juxiang，XING Zhina，et al.The investigation on research progress and development of fuel cell[J].Energy Conservation Technology，2010，28（4）：1-5（in Chinese）.

[3]运输司.交通运输部关于加快推进新能源汽车在交通运输行业推广应用的实施意见[EB/OL].http://www.moc.gov. cn/zfxxgk/bnssj/dlyss/201503/t20150318_1790182.htm l，2015-03-13.

[4] TOMIC J，KEMPTON W.Using fleets of electric-drive vehicles for grid support[J].Journal of Power Sources，2007，168（2）:459-468.

[5]李菱，唐朝裕，李笑怡.基于粒子群遗传算法的电动汽车充电站的布局规划[J].陕西电力，2014，42（4）：65-69. LI Ling，TANG Chaoyu，LI Xiaoyi.Layout planning of electrical vehicle charging stations based on particle swarm genetic algorithm[J].Shaanxi Electric Power，2014，42（4）：65-69（in Chinese）.

[6]马玲玲，杨军，付聪，等.电动汽车充放电对电网影响研究综述[J].电力系统保护与控制，2013，41（3）:140-148. MA Lingling，YANG Jun，FU Cong，et al.Review on impact of electric car charging and discharging on power grid[J].Power System Protection and Control，2013，41（3）:140-148（in Chinese）.

[7]艾明浩，齐林海.基于有序充电的电动汽车充电站在线监控系统[J].陕西电力，2014，42（6）：6-11. AIMinghao，QILinhai.Electric vehicle charging stations’on-line monitoring system based on ordered charging[J]. Shaanxi Electric Power，2014，42（6）：6-11（in Chinese）.

[8]刘严，谭忠富，乞建勋.峰谷分时电价设计的优化模型[J].中国管理科学，2005，13（5）:87-92. LIU Yan，TAN Zhongfu，QI Jianxun.Research on TOU rate design optimization model[J].Chinese Journal of Management Science，2005，13（5）:87-92（in Chinese）.

[9]葛少云，黄镠，刘洪.电动汽车有序充电的峰谷电价时段优化[J].电力系统保护与控制，2012，40（10）：1-5. GE Shaoyun，HUANG Liu，LIU Hong.Optimization of peak-valley TOU power price time-period in ordered chargingmode of electric vehicle[J].Power System Protection and Control，2012，40（10）：1-5（in Chinese）.

[10]项顶，宋永华，胡泽春，等.电动汽车参与V2G的最优峰谷电价研究[J].中国电机工程学报，2013，33（31）: 15-25. XIANG Ding，SONG Yonghua，HU Zechun，et al.Research on optimal time of use price for electric vehicle participating V2G[J].Proceedings of the CSEE，2013，33（31）:15-25（in Chinese）.

[11]戴诗容，雷霞，程道卫，等.电动汽车峰谷分时充放电电价研究[J].电网与清洁能源，2013，29（7）：77-91. DAIShirong，LEIXia，CHENG Daowei，et al.Study on electric vehicle charging and discharging TOU price[J]. Power System and Clean Energy，2013，29（7）：77-91（in Chinese）.

[12]高亚静，王辰，吕孟扩，等.计及车主满意度的电动汽车最优峰谷分时电价模型[J].电力自动化设备，2014，34（2）:8-12. GAO Yajing，WANG Chen，LÜMengkuo，et al.Optimal time-of-use price model considering satisfaction degreeof electric vehicle owners[J].Electric Power Automation Equipment，2014，34（2）:8-12（in Chinese）.

[13]田立亭，史双龙，贾卓.电动汽车充电功率需求的统计学建模方法[J].电网技术，2010，34（11）:126-130. TIAN Liting，SHI Shuanglong，JIA Zhuo.A statistical model for charging power demand of electric vehicles[J]. Power System Technology，2010，34（11）:126-130（in Chinese）.

[14]VYAS A，SANTINI D.Use of national surveys for estimating‘full’PHEV potential for oil use reduction[EB/ OL].2008-07-21[2013].Http://www.transporttation.anl.gov/ pdfs/-HV/525.pdf.

[15]孙波，廖强强，谢品杰，等.车电互联削峰填谷的经济成本效益分析[J].电网技术，2012，36（10）:30-34. SUN Bo，LIAO Qiangqiang，XIE Pinjie，et al.A costbenefitanalysismodelofvehicle-to-grid for peak shaving[J]. Power System Technology，2012，36（10）:30-34（in Chinese）.

[16]秦祯芳，岳顺民，余贻鑫.零售端电力市场中的电量电价弹性矩阵[J]．电力系统自动化，2004，28（5）：16-19. QIN Zhenfang，YUE Shunmin，YU Yixin.Price elasticity matrix of demand in current retail power market[J].Automation of Electric Power Systems，2004，28（5）：16-19（in Chinese）.

[17]丁伟，袁家海，胡兆光.基于用户价格响应和满意度的峰谷分时电价决策模型[J].电力系统自动化，2005，29（20）：10-14. DINGWei，YUAN Jiahai，HU Zhaoguang.Time-of-use price decision model considering user’s reaction and satisfaction index[J].Automation of Electric Power Systems，2005，29（20）：10-14（in Chinese）.

[18]王勇，蔡自兴，周育人.约束优化进化算法[J].软件学报，2009，20（1）：11-29. WANG Yong，CAI Zixing，ZHOU Yuren.Constrained optimization evolutionary algorithm[J].Journal of Software，2009，20（1）：11-29（in Chinese）.

[19]袁晓辉，王乘，张勇传，等.粒子群优化算法在电力系统中的应用[J].电网技术，2004，28（19）：14-19. YUAN Xiaohui，WANG Cheng，ZHANG Yongchuan，et al.A Survey on application of particle swarm optimization to electric power systems[J].Power System Technology，2004，28（19）：14-19（in Chinese）.

[20]李惠玲，白晓民.电动汽车充电对配电网的影响及对策[J].电力系统自动化，2011，35（17）：38-43. LI Huiling，BAI Xiaomin.Impacts of Electric Vehicles Charging on Distribution Grid[J].Automation of Electric Power Systems，2011，35（17）：38-43（in Chinese）.

[21]胡泽春，宋永华，徐智威，等.电动汽车接入电网的影响与利用[J].中国电机工程学报，2012，32（4）：1-10. HU Zechun，SONG Yonghua，XU Zhiwei，et al.Impacts and utilization of electric vehicles integration into power systems[J].Proceedings of the CSEE，2012，32（4）：1-10（in Chinese）.

SynchronousOptim ization M odel for the Time-of-Use Price of Charge and Discharge of Electric Vehicles

SUN Bo，WANG Zhenxing，SUN Jiajia
（
School of Economics and Management，Shanghai University of Electric Power，Shanghai200090，China）

Load curve is random ly varied when electric vehicles（EVs）access the grid without any guidingmechanism，and as a result that the controlwill bemore difficult.By establishing appropriate Time-of-use（TOU）price of charge and discharge of EVs，the users can be led to participate in the charge and discharge of the power grid in different time intervals，and this is good for peak-shaving.First，a powermodel of a single electric vehicle’s random charge and discharge is established by Monte Carlo simulation，and the impact of the mass accessing of EVs to the power grid on the system load is analyzed.Furthermore，the synchronous optimization model for the TOU price of charge and discharge is constructed and the interaction between the electricity consumption and electricity price is established and the synchronous optimization on the price of charge and discharge is realized.Finally，the PSO algorithm is used to solve themodel.The numerical examples show that the goal of peak-shaving can be reached through the strategy of the synchronous optimization on the TOU price of charge and discharge and at the same time revenue of EV users can be increased.

peak-shaving；charge and discharge price；synchronous optimization；Monte Carlo simulation；PSO

2015-09-06。

孙 波（1982—），女，副教授，从事最优化及智能电网需求侧管理研究；

（编辑 徐花荣）

国家自然科学基金青年项目（51507099）；上海市教委科研创新项目（13YS092）；上海市社科规划一般课题（2015BGL002）。

Project Supported by the National Natural Science Foundation for Young Scholars（51507099）；the Scientific Innovation Program of ShanghaiMunicipal Education Commission（13ys092）；General Subject of the Social Science Planning of ShanghaiMunicipality（2015BGL002）.

1674-3814（2017）02-0130-07

TM73

A

王振兴（1989—），男，硕士研究生，从事车电互联电价机制研究。