基于二层规划的电力系统无功优化混合算法研究

唐永红，李旻，姜振超，路轶，范宏，季昕雨，陈斯

（1.国网四川省电力公司电力科学研究院，四川成都 610072；2.智能电网四川省重点实验室，四川成都 610072；3.国网四川省电力公司调度控制中心，四川成都 610041；4.上海电力学院电气工程学院，上海 200090）

基于二层规划的电力系统无功优化混合算法研究

唐永红1，2，李旻3，姜振超1，2，路轶3，范宏4，季昕雨4，陈斯4

（1.国网四川省电力公司电力科学研究院，四川成都 610072；2.智能电网四川省重点实验室，四川成都 610072；3.国网四川省电力公司调度控制中心，四川成都 610041；4.上海电力学院电气工程学院，上海 200090）

二层规划；无功优化；内点法；森林算法；检测平台

电力无功功率的合理分布，关系到系统电压水平和网损大小，是电力系统安全与经济运行的重要保障。电力系统无功优化，即以保证电力系统电压质量为前提，利用无功补偿优化电网无功潮流，使系统的有功损耗和无功补偿费用最小。

国内外学者对无功优化问题的研究主要在于优化模型与实现算法，取得了较大成果，但仍然存在许多问题。电力系统无功优化问题的精确数学模型描述为一个非线性、既含连续变量又含离散变量的大规模混合整数优化问题。从模型上看，在满足系统基本运行条件的前提下，根据不同的运行要求，可以选择不同的目标函数。从系统经济性角度出发选取系统的有功损耗或无功损耗最小为目标函数；从系统的安全性角度出发选取节点电压偏离规定值最小为目标函数。另外，根据不同的运行要求，还必须包含大量的等式和不等式约束条件[1]。一般无功优化的标准数学模型为式中：f（x1，x2，…，xn）为目标函数；h（x1，x2，…，xn）为等式约束条件，一般为潮流方程；g（x1，x2，…，xn）为不等式约束条件，一般为线路传输功率约束、发电机功率约束和无功补偿容量约束。

从求解方法上看，含离散变量的优化问题难以求解，如何有效地求解这一类组合优化问题，一直是许多学者研究的热点[2-6]。目前主要的求解方法包括线性规划法、非线性规划法、混合整数规划法及人工智能算法等。

1 二层规划数学模型

1.1 二层规划原理

二层规划是一种特殊的多层规划[7]，上下层模型根据其内在联系相互影响、相互制约。上层的决策变量为下层的目标函数，即上层在下层的最优决策基础上，实现总目标函数；下层的目标函数和可行集受到上层的约束。同时，下层的决策也将影响到上层的目标函数，二者相互制约、相互影响，最终达到全局的最优。

上述描述中可以得知，二层规划尤其适用于多目标优化的情况，对于多目标函数的问题，每个决策变量对不同目标的影响大小不同。各个目标函数之间也有相互影响的关系，二层规划就是利用多目标之间的这种关系，结合决策变量的特点，将系统分为2层，上层问题的目标函数为总目标函数，根据该层的决策变量、可行域等做出决策；下层的目标函数为上层决策变量的一部分，受到上层制约，每层根据各自目标函数，调整自己的决策变量，获得目标函数的最大化。

1.2 二层规划的数学模型

电力系统中电压分布与无功分布联系密切，调节无功电源的出力会影响网络中无功潮流的分布，保证无功功率的就地平衡，对减小线路中传输的无功功率，进而减小线路中的有功损耗和电压损耗有十分显著的意义。调节变压器分接头则会直接影响到系统电压水平，但这种调节方式往往是局部的，在整个系统中无功电源没有多发的情况下，局部厂站的电压升高必然会带来其他地区电压的下降[7]。

本论文无功优化的二层模型在设计上充分考虑了电网无功电压调节的实际情况，在实际电力系统中，一些分站、分线只着眼于几个关键母线的电压指标，为满足自身利益盲目调节，没有从整个系统的角度进行电压无功的综合优化，有可能导致系统电压问题更加严重。二层规划的特点恰是从整体角度出发，将整个系统按照目标函数分层考虑，打破既有的每个厂站各自调节的局限，既保证了系统对降低网损的需求，又考虑了电压。

上层目标函数和约束条件：

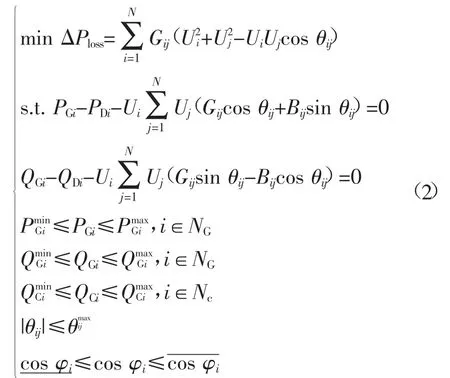
下层目标函数和约束条件：

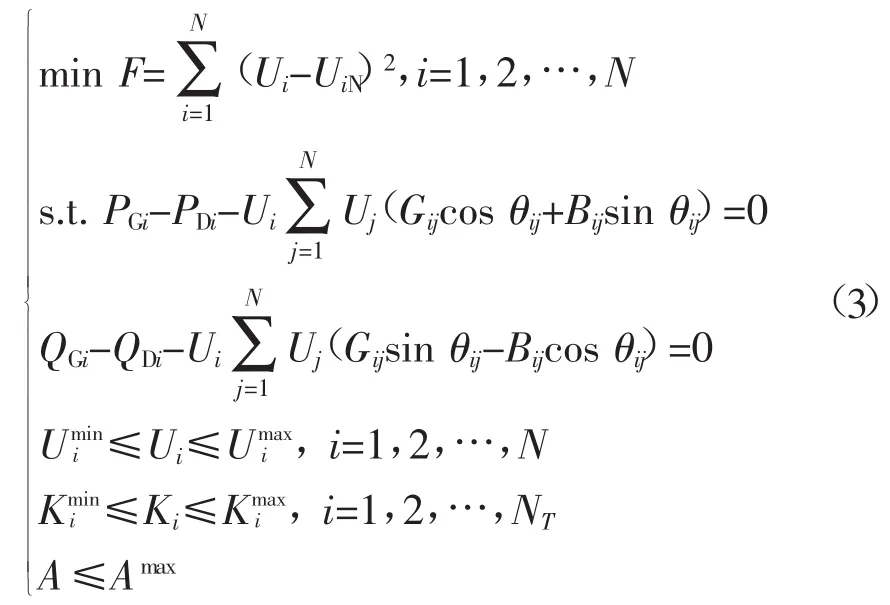
式中：F为下层模型的目标函数，即各节点电压与额定电压之差的平方；Ui为节点电压幅值；UiN为各节点电压的期望水平；N为系统节点数；NG为发电机节点集合；NC为具有无功补偿设备的节点集合；NT为变比可调的变压器个数；gij为支路ij的电导；Gij、Bij为节点导纳矩阵中的元素；θij为节点ij间的电压相角差；θmaxij为相角差的最大允许值；为关口功率因数下限；为 关口功率因数上限；PDi、QDi为节点的负荷有功和无功功率；PGi、QGi分别为发电机有功和无功出力；QCi为无功补偿设备的无功出力分别为相应变量的上、下限。

2 优化算法的选择

电力系统无功优化问题的精确数学模型描述为一个非线性、既含连续变量又含离散变量的大规模混合整数优化问题。上层模型中决策变量为发电机和无功补偿设备的无功出力，通过调节无功电源的出力，使整个电网的无功处于合理的水平。由于无功电源多为连续变量，相当于在变压器档位给定情况下的连续优化问题，适合用原对偶内点法。下层模型目标函数为各节点电压偏移最小，相当于在整个电网无功水平合理情况下对节点电压的微调，使各节点电压处于更加理想的水平，决策变量为变压器档位，为离散变量，利用随机森林算法可以取得较好的结果。

2.1 原-对偶内点法

内点法的基本原理是通过在可行域边界设置障碍函数，使每一步迭代过程中，若解接近边界，其目标函数会迅速增大，从而保证解始终在可行域内。一个优化问题（原问题），总可以找到一个与其对应的对偶问题，同时，解在对偶间隙为零时取得。这样，就能够通过对偶间隙来判断迭代的收敛情况。为了便于说明，我们考虑如下形式的非线性规划问题：

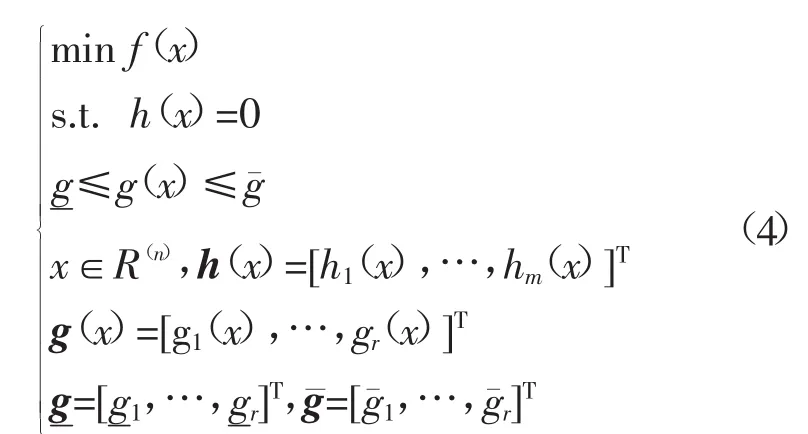
首先，引入松弛矢量，将不等式约束转化为等式约束，则问题（4）转换为

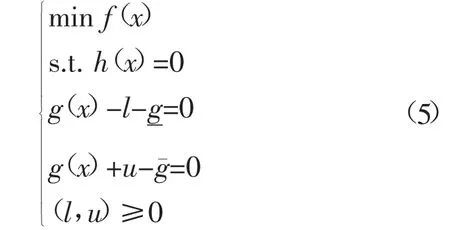
其次，定义一个与式（5）相联系的拉格朗日函数：L（x、l、u、y、z、w，z~，w~）=f（x）－yTh（x）－zT[g（x）+u－g¯]－wT[g（x）+u－g¯]－z~Tl－w~Tu，其中y∈R（m），（z、w、z~，w~）∈R（r）是language乘子。

然后，根据KKT一阶最优性条件，我们能够导出KKT方程：

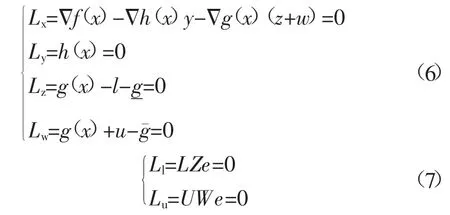
式中：（l、u，z）≥0，w≤0，y≠0，（L、U、Z，W）∈Rr×r是对角阵；Lx为，其余形式同理。

接着，引入一个扰动因子μ＞0去松弛互补条件（5），得到：

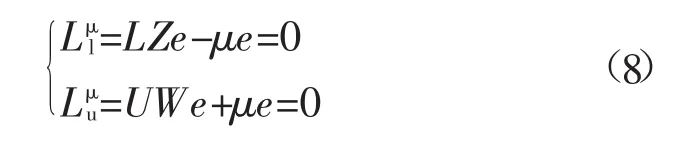
然后，应用newton法解由（6）和（8）组成的扰动KKT方程，得到如下的修正方程：

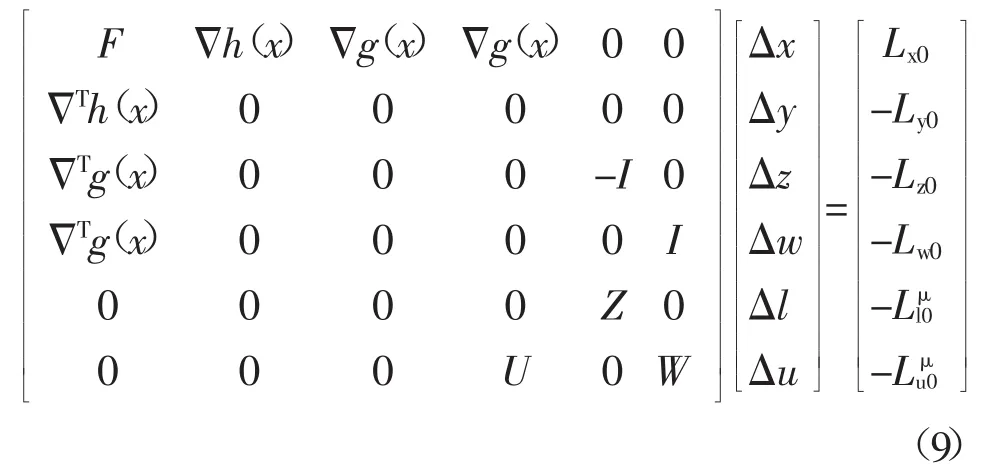
解修正方程（9）得到第k次迭代修正量，更新原始对偶变量，则第k次迭代的最优解为

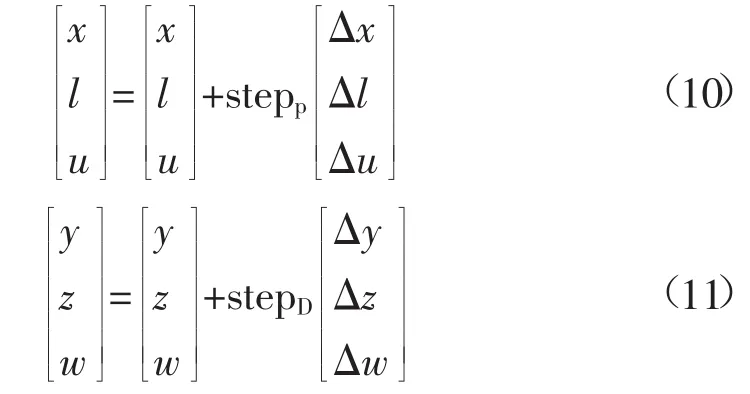
式中：stepp和stepD分别为原始步长和对偶步长，按以下公式选择在，以保证原始-对偶变量的可行性：

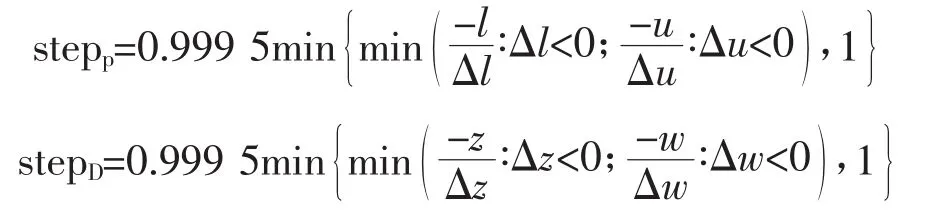
2.2 随机森林算法

随机森林算法（random forest algorithm，RF）是一类组合决策树分类器的方法，由Breiman[8]提出。RF组合多棵决策树做出预测，其中每棵树都是基于随机向量的一个独立集合的值，该算法具有较少参数调整、可避免过度拟合、能估计哪个特征在分类中更重要及等优点[9]。

决策树从一组无规则的事例经推理得出树状的分类规则。树的根节点是整个数据集合空间，采用自顶向下的递归方式，在每个内部节点上对属性测试，并根据不同分类规则将该节点分为2支或多支，最后在每个叶节点得到结论[10]。决策树的生长采用二分递归分割的技术，每个结点（除叶结点外）都将当前样本集划分为2个子样本集。随机森林中的所有决策树均为结构简单的二叉树[11]。

每一棵决策树都对应一个训练集，随机森林算法采用有放回随机抽样的方法从原始训练集中产生N个子集，这N个子训练集对应这N棵决策树。每个训练子集的大小约为原始训练集的4/5，这样，可以保证随机森林中的每一训练子集都有一定的重复，避免产生局部最优解[12]。

本模型中，以变压器档位为变量，随机生成N棵树，组成训练集，求取网络中节点电压对变压器档位的灵敏度δ：

式中：Ui为节点i的电压幅值；Kj为变压器j的变比。这样，对于节点i的电压，δij＞0时，电压Ui随着变压器j的档位提升而升高，随着变压器j的档位下降而下降；δij＜0时则相反。生成决策树过程中，随机选择某一变压器的档位灵敏度δj，按照δj的正负分裂当前节点，将训练集分为2个子集，生成2个根节点，再随机选择某一变压器的档位灵敏度δk，重复上述步骤，直到当前训练集的所有样本都属于相同的类别，或样本属性集合为空，算法结束。

3 基于SCADA的大电网无功优化闭环检测平台测试

文中算法在基于SCADA的大电网全数字无功优化检测平台上进行了比对测试。该平台连接实时数字电网仿真系统与OPEN3000系统，能够对实际电网进行实时、在线的模拟仿真和评估，分别利用文中提出的二层优化算法和OPEN3000系统中的AVC优化策略对电网的实际工况进行比对，比较不同控制策略的控制结果[13]。系统平台由系统配置模块、基础数据库模块、实时数据库模块、计算与数据接口模块等构成，如图1所示。

图1基于SCADA的ADPSS仿真数据平台示意图Fig.1 The schematic diagram of ADPSS simulation data p latform based on SCADA

文中以OPEN3000系统中嵌入式AVC系统的优化策略为参考，综合评价二层优化算法。综合仿真程序ADPSS输出的数据经中间数据转换装置转换为IEC104规约数据[14]，作为AVC系统的原始数据，同时，二层优化算法程序解析相同数据，对当前潮流断面进行优化，分别给出相应控制策略[15]。

无功优化平台包括仿真数据平台、计算服务器、百兆以太网交换机、AVC系统工作站、外部通信服务器、评估服务器等6部分。其中计算服务器也具备有数据库服务和事件调度服务，服务器之间的通信采用基于中间件技术的软总线连接。

在并行仿真计算初始化时运行一次全网拓扑分析，在仿真过程中如果有开关变位或者设备投退等操作会触发变化拓扑中间件接口。服务器与外部通信接口基于调度104规约，采取长连接形式，保证通信稳定可靠。

4 算例

文中采用IEEE30标准节点系统以及四川某地区电网验证该算法的有效性及正确性。其中IEEE30标准节点系统具有发电机6台，变压器4台，交流线路37条。采用IEEE30标准节点系统对二层规划算法的正确性进行验证。四川某地区电网含有152节点，等值发电机20台，变压器74台，交流线路40条。为综合比较算法的优化效果，文中调试了四川某地区电网若干典型工况，计算其优化结果，并与AVC优化算法的结果进行对比。

案例一：对IEEE30标准节点系统分别采用潮流计算和二层规划法计算，以验证二层规划算法的正确性。表1为变压器调节状态；表2为优化前后无功电源出力变化；图2为采用二层规划算法的IEEE30标准节点系统的计算收敛曲线；图3为采用二层规划算法的优化前后电压分布图。由表1和表2可知，变压器变比以及无功电源出力均在约束范围之内，满足要求。

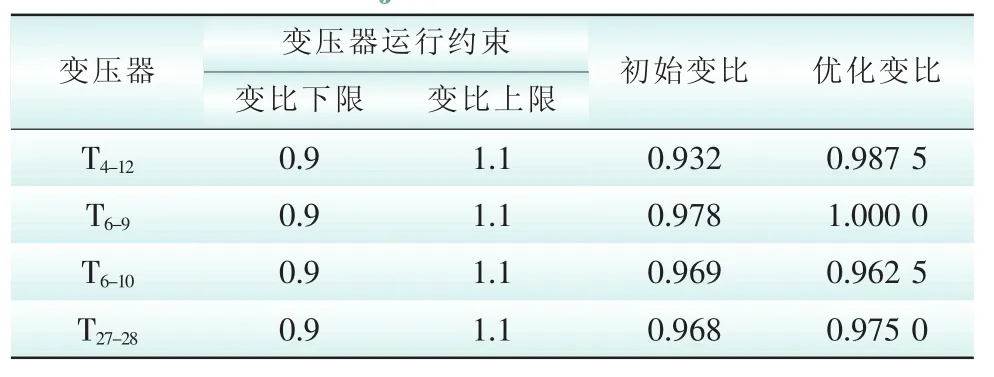
表1 变压器变比调整情况Tab.1 The ad justment of transformer ratio

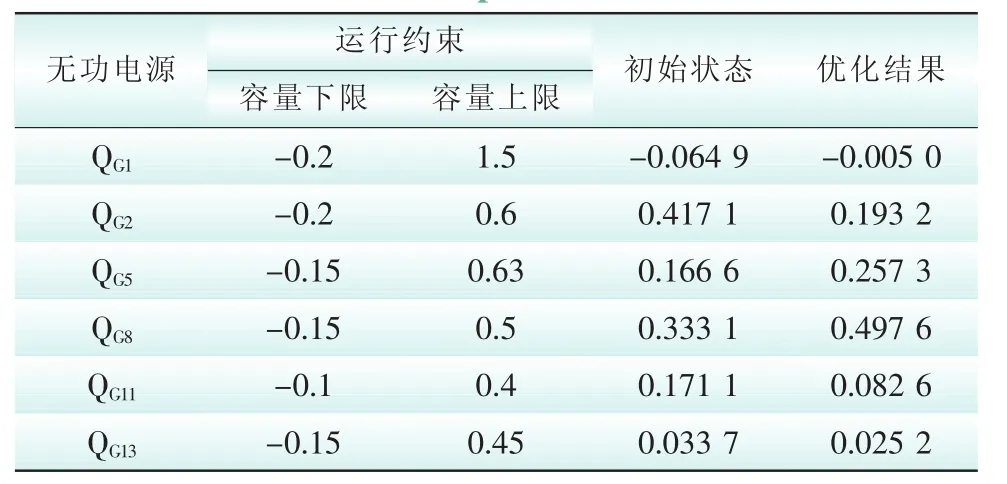
表2 优化前后无功电源出力变化Tab.2 The variation of reactive power outputbefore and after optim ization MV·A

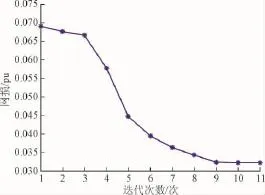
图2 IEEE30标准节点系统的算法收敛曲线Fig.2 The algorithm convergence curve of IEEE 30 standard node

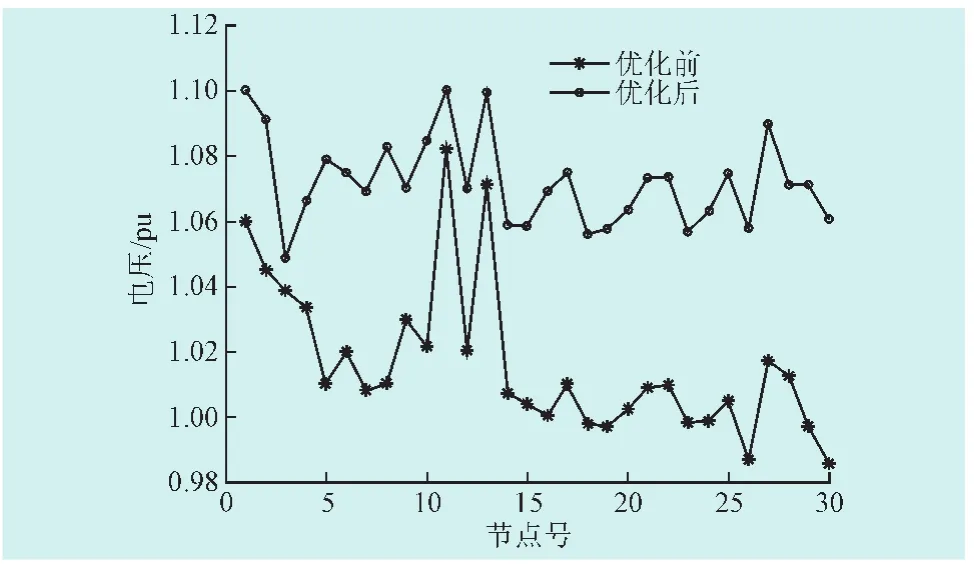
图3 优化前后电压分布图Fig.3 The voltage distribution before optim ization and after optim ization

由图2可知，二层规划算法在迭代到第10次时即收敛，表明二层规划算法的求解收敛性较高。二层规划算法优化后；如图3所示，系统中电压基本维持在1.05 pu。系统网损从初始的0.053 7下降到0.032 3，说明二层规划算法在降低网损、提高电压合格率方面有较显著的效果。

案例二：四川某地区电网全网电压低。在基础潮流的基础上，调节全网负荷为基础潮流的1.3倍，使全网电压普遍偏低，6条母线电压越下限，同时8台主变无功欠补。这时，系统总网损为12.585 MW。测试二层优化算法与AVC优化算法对系统的调节效果，比较2种策略的母线电压、关口功率因数和网损。

由表3可知，二层规划算法对于此运行方式的控制结果优于AVC优化算法。该策略投入了马井站的电容2路和电容4路，投入相邻110 kV雒城站、炳灵宫站和220 kV新市站、孟家站的部分电容，并将古城站的主变由3档升为4档，比AVC优化算法的动作次数更少，且网损的降低较初始潮流也十分显著，同时网损值较AVC优化算法有所减少。因为二层规划算法是基于全局的优化方法，全局寻优能力强，能够在所有解空间内寻找最优值，对于无功功率分散就地补偿，从而避免陷入局部最优，该案例表明二层优化算法具有很强的适应性[16-17]。

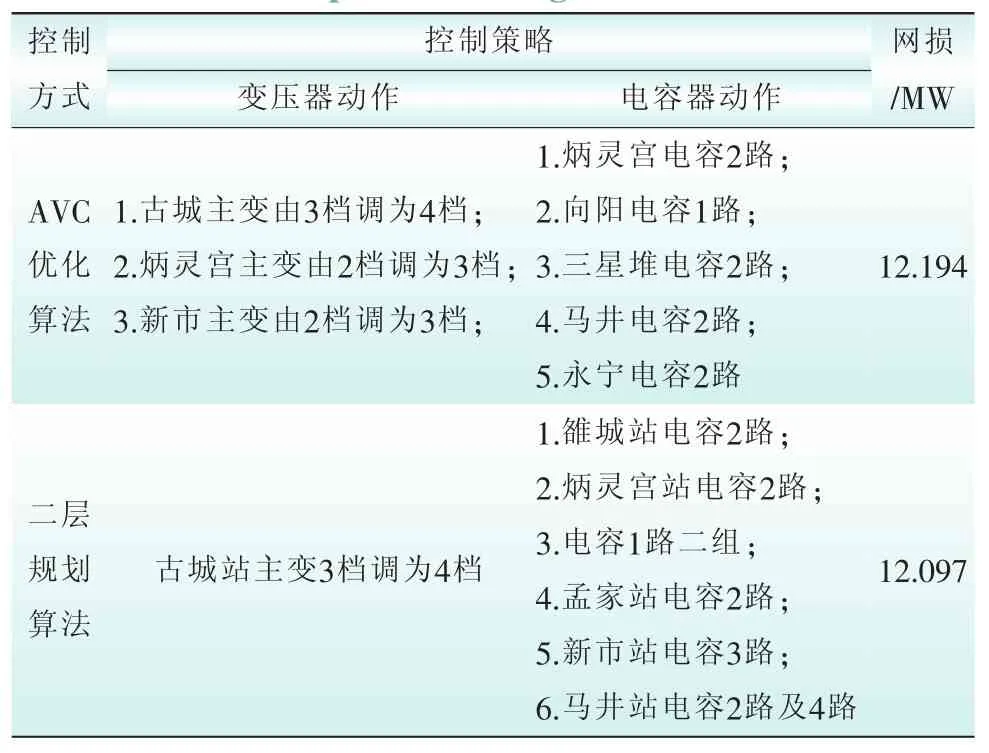
表3 各控制算法策略对比Tab.3 The control strategy comparison between AVC optim ization algorithm and bi-level programm ing optim ization algorithm

由表4、表5可知，二层规划算法的动作策略能够使关口功率因数和节点电压水平提升到目标范围以内，动作策略可靠、有效。

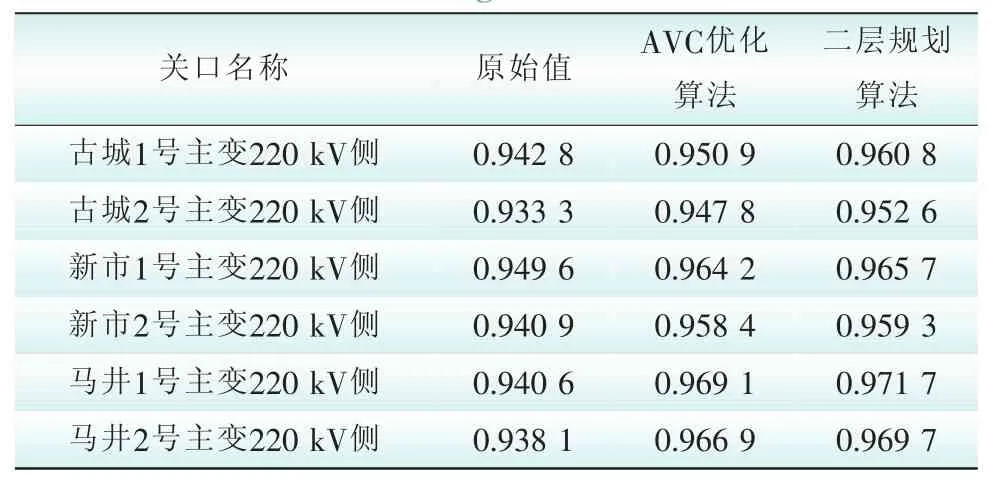
表4 2种策略关口功率因数结果对比Tab.4 The power factor com parison between two algorithm s

综上，对于全网负荷重、电压水平低的工况，二层规划算法能够比AVC优化算法更好地调整系统无功，降低系统网损，表明二层规划算法的综合优化性能更优。

5 结论

文中提出了一种基于二层规划模型的电力系统无功优化方法，充分结合电力系统实际需求，针对不同目标函数、变量提出了不同的优化算法，上层利用原-对偶内点法求解，下层利用随机森林算法求解，实际案例表明，该算法可以显著降低电力系统的网损，提高电压合格率。

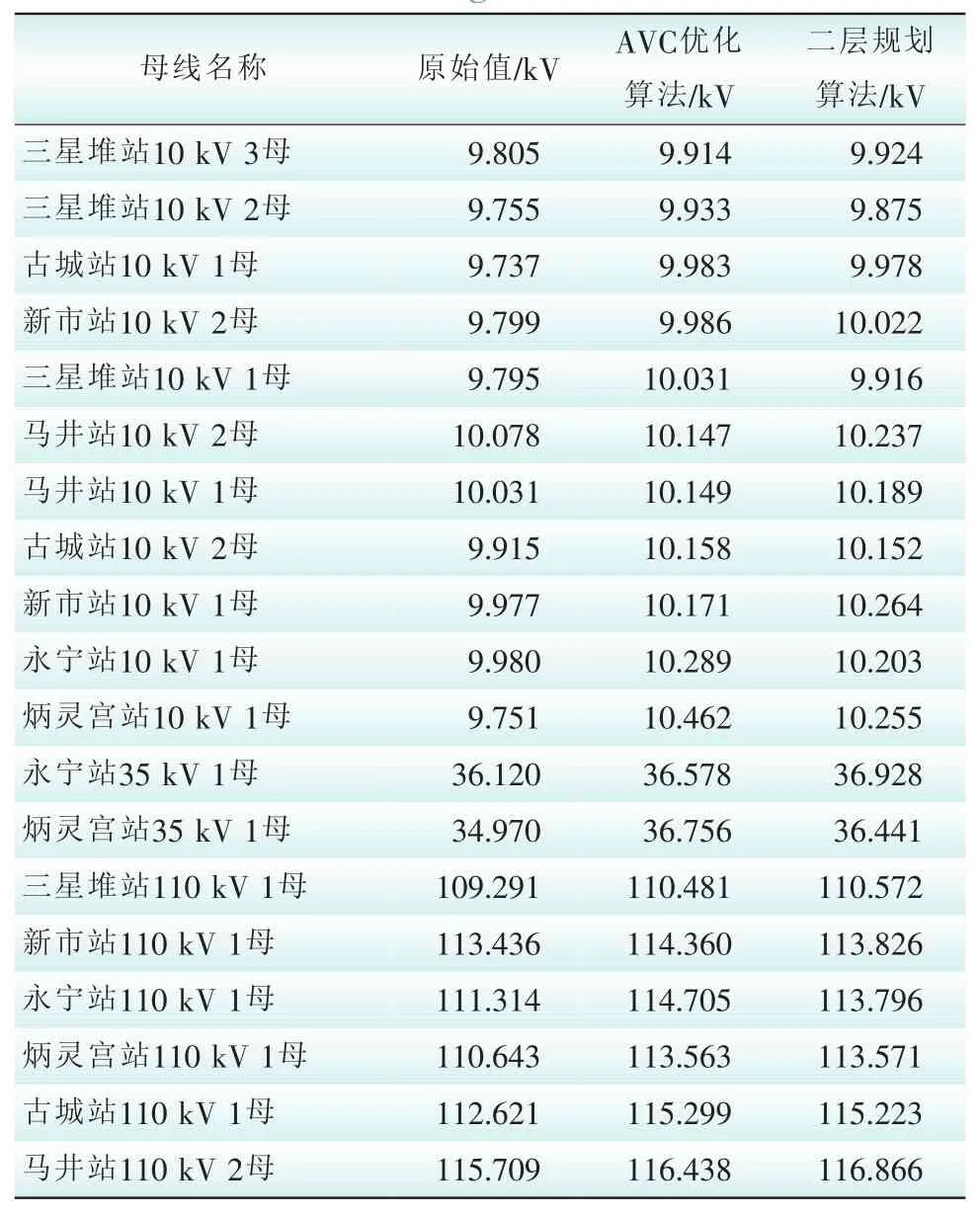
表5 2种控制策略下各条母线电压对比Tab.5 The bus voltage com parison between two algorithm s

[1] 刘方，颜伟，David C.YU.基于遗传算法和内点法的无功优化混合策略[J].中国电机工程学报，2005，25（15）: 67-72. LIU Fang，YAN Wei，David C，YU.A hybrid strategy based on GA and IPM for optimal reactive power flow[J]. Proceedings of the CSEE，2005，25（15）：67-72（in Chinese）.

[2]许诺，黄民翔.原对偶内点法与定界法在无功优化中的应用[J].电力系统及其自动化学报，2000，12（3）:26-30. XU Nuo，HUANG Minxiang.Application of primal-dual interior pointmethod and branch-bound method in reactive power optimization[J].Proceedings of the CSU-EPSA，2000，12（3）:26-30（in Chinese）.

[3]HUAWei，SASAKIH，KUBOKAWA J，etal.An interiorpoint nonlinear programming for optimal power flow problemswith a novel data structure[J].IEEE Transactions on Power Systems，1998，13（3）：870-877.

[4]王晓东，李乃湖，丁恰.基于稀疏技术的原对偶内点法电压无功功率优化[J].电网技术，1999，23（3）：23-26，30. WANG Xiaodong，LI Naihu，DING Qia.A primal-dual interior point method for optimal voltage/reactive power control with sparsity structure[J].Power System Technology，1999，23（3）:23-26，30（in Chinese）.

[5]GRANVILLE S.Optimal reactive dispatch through interior point methods[J].IEEE Transactions on Power Systems，1994，9（1）:136-146.

[6] BARD JF.Practical bi-level optimization algorithms and applications[M].Kluwer Academic Publishers，1998．

[7]王淑芬，万仲平，樊恒，等.基于二层规划的无功优化模型及其混合算法[J].电网技术，2005，29（9）：22-25. WANG Shufen，WAN Zhongping，FAN Heng，et al. Reactive power optimization model and its hybrid algorithm based on bi-level programming[J].Power System Technology，2005，29（9）:22-25（in Chinese）.

[8]方匡南，吴见彬，朱建平，等.随机森林方法研究综述[J].统计与信息论坛，2003，26（3）:32-36. FANG Kuangnan，WU Jianbin，ZHU Jianping，et al.A review of technologies on random forests[J].Statistics& Information Forum，2003，26（3）:32-36（in Chinese）.

[9]叶圣永，王晓茹，刘志刚，等.基于随机森林算法的电力系统暂态稳定性评估[J].西南交通大学学报，2008，43（5）:573-577. YE Shengyong，WANG Xiaoru，LIU Zhigang，et al. Transient stability assessment based on random forest algorithm[J].Journal of Southwest Jiaotong University，2008，43（5）:573-577（in Chinese）.

[10]Carolin Strobl，Anne-Laure Boulesteix，Achim Zeileis，et al.Bias in random forest variable importance measures: illustrations，sources and a solution[J].BMC Bioinformatics，2007，8（1）:1-21.

[11]UMEZAWA Y，MORIH.Credit risk evaluation of power market players with random forest[J].IEEJTransactions on Power&Energy，2008，128（1）:165-172.

[12]马景义，吴喜之，谢邦昌.拟自适应分类随机森林算法[J].数理统计与管理，2010，29（5）:805-811. MA Jingyi，WU Xizhi，XIE Bangchang.Quasi-adaptive random forest for classification[J].Journal of Applied Statistics and Management，2010，29（5）:805-811（in Chinese）.

[13]唐永红，徐琳，范宏，等.基于实时仿真系统的地区电网AVC系统闭环检测方法[J].电网技术，2013，37（9）: 2515-2520. TANG Yonghong，XU Lin，FAN Hong，et al.Real-time simulation based closed-loop detection for AVC system of regional power grid[J].Power System Technology 2013，37（9）：2515-2520.

[14]栗杰鹏，陈天华，杜磊，等.基于区域策略寻优的地区电网AVC系统[J].江苏电机工程，2013，32（3）:30-32. LI Jiepeng，CHEN Tianhua，DU Lei，et al.AVC system for regional power grid based on regional strategy optimization[J].Jiangshu Elecrtical Engingeerying，2013，32（3）:30-32.

[15]张望，徐岩，孟科，等.能源互联网中基于多微网校正控制的安全约束最优潮流[J].南方电网技术，2016，10（8）:67-73. ZHANG Wang，XU Yan，MENG Ke，et al.SCOPF for corrective control using multimicrogrids in energy internet[J].Southern Power System Technology，2016，10（8）: 67-73（in Chinese）.

[16]黄晨，张靠社.基于量子粒子群算法的微电网优化调度[J].电网与清洁能源，2016（2）:72-76. HUANG Chen，ZHANG Kaoshe.Micro grid scheduling optimization based on quantum particle swarm optimization（PSO） algorithm[J].Power System and Clean Energy，2016（2）:72-76（in Chinese）.

[17]林捷，王云柳，黄辉，等.自动电压控制下的地区电网电压无功运行状态评估指标体系[J].电力系统保护与控制，2016，44（13）:123-129. LIN Jie，WANG Yunliu，HUANG Hui，et al.An index system for voltage and reactive power operation status evaluation in regional power grid under automatic voltage control[J].Power System Protection and Control，2016，44（13）：123-129（in Chinese）.

A Hybrid Algorithm for Reactive Power Optim ization Based on Bi-Level Programm ing

TANG Yonghong1，2，LIMin3，JIANG Zhenchao1，2，LU Yi3，FAN Hong4，JIXinyu4，CHEN Si4
（1.State Grid Sichuan Electric Power Research Institute，Chengdu 610072，Sichuan，China；2.Intelligent Electric Power Grid Key Laboratory of Sichuan Province，Chengdu 610072，Sichuan，China；3.State Grid Sichuan Electric Power Dispatch and Control Center，Chengdu 610041，Sichuan，China；4.Deptof Electric Power Engineering，ShanghaiUniversity of Electric Power，Shanghai200090，China）

In this paper，a bi-level programmingmodel for reactive power optimization is established based on the characteristicsof the grid voltage-reactive power control.Themini-mum grid loss and the minimum voltage offset are selected as the objective functionsfortheupper-leveland lower-levelres-pectively. Accordingtothe differencesof the solution spaceof the two levels，the primal-dual interior pointalgorithm is re-commended for the upper-level while random forests algorithm （RFA）for the lower-level.A reactive power optimization closed-loop detection platform is established based on advanced digitalpower system simulator（ADPSS）foracomprehensivecomparativeanalysisofthe optimization strategyof thebi-level programming proposed in the paperand theembedded AVCsystem in theOPEN30000.

bi-level programming；reactive power optimization；interior pointalgorithm；forests algorithm；test platform摘要：结合电力系统电压无功综合调控特点，建立无功优化的二层规划模型。上、下层分别选取系统网损最小和各节点电压偏移最小为目标函数，根据上、下层解空间的不同，上层采用原-对偶内点法，下层采用森林算法。搭建基于电力系统全数字实时仿真装置（ADPSS）的无功优化闭环检测平台，综合对比分析文中提出的二层规划程序和OPEN3000中的嵌入式AVC系统的优化策略，结果表明：该算法可以显著将低电力系统的网损，提高电压合格率。

2016-11-20。

唐永红（1965—），女，学士，高级工程师，主要研究方向为电网仿真分析、电力系统设备检测；

（编辑 张晓娟）

四川省电力公司2015科技支撑项目《AVC应用评价系统开发及全程极限控制策略研究》（52199713506C）。

Project Supported by 2015 Science and Technology Project of Sichuan Electric Power Company“Development of AVC application Evaluation systems and Research on Full-Range Extreme Control Strategies”（52199713506C）.

1674-3814（2017）02-0037-07

TM761.1

A

李 旻（1970—），男，硕士，高级工程师，主要研究方向为电网稳定运行、电力市场和节能发电调度。