基于遗传算法的VSC-HVDC控制系统PI参数优化

崔静思，高凯，韩子娇，张艳军，陈艳波，马进

（1.国网天津市电力公司东丽供电分公司，天津 300300；2.国网辽宁省电力有限公司，辽宁沈阳 110006；3.华北电力大学，新能源电力系统国家重点实验室，北京 102206；4.悉尼大学电气与信息学院，悉尼NSW，2006，澳大利亚）

基于遗传算法的VSC-HVDC控制系统PI参数优化

崔静思1，高凯2，韩子娇2，张艳军2，陈艳波3，马进4

（1.国网天津市电力公司东丽供电分公司，天津 300300；2.国网辽宁省电力有限公司，辽宁沈阳 110006；3.华北电力大学，新能源电力系统国家重点实验室，北京 102206；4.悉尼大学电气与信息学院，悉尼NSW，2006，澳大利亚）

针对采用直接电流控制策略的电压源换流器（voltage source converter，VSC）控制系统比例积分（PI）参数难以选取的问题，提出了一种优化外环PI控制器参数的方法。首先建立解耦后的外环参数整定模型，然后基于时间乘绝对误差积分（integral of time multiplied by the absolute value of error，ITAE）准则构造PI参数优化的性能泛函，针对此最优控制模型的特点，论文采用遗传算法进行求解，在PSCAD搭建VSC-HVDC模型进行仿真验证。

VSC；PI控制器；整定模型；遗传算法

基于电压源换流器的高压直流输电（voltage source converter based high voltage direct current，VSC-HVDC）由于采用了可自关断的可控器件，因而具有有功和无功快速独立的控制，潮流反转方便快捷，可提高现有交流系统的输电能力及功角稳定性等优点。自20世纪90年代以来，VSC-HVDC得到了快速发展和应用[1-2]。

目前对于VSC主要采用直接电流控制策略，可分解为内环控制器和外环控制器[3]。其PI控制器结构简单；在实际过程中PI参数的整定常采用试凑法或经验法，操作和调节时需较高的经验和技巧，不易获得满意效果[2]。比例控制能迅速反应误差，快速减小稳态误差，比例放大系数过大会引起输出响应的超调不稳定。只要响应有误差存在，积分控制器就不断地积累，输出控制量以消除误差。选择合适的PI参数对优化VSC的控制性能、发挥VSC的优势具有重要意义[4]。

目前国内外对如何优化VSC控制器中的PI参数的研究还未充分展开。文献[5]根据Bode图求出满足系统稳定性要求的PI参数可行域，但其优化效果受可行域划分步长的影响。文献[6]将粒子群算法与直流输电仿真模型结合进行仿真计算，获得较优的控制器参数，但该方法所需时间较长，实用性较低。文献[7]将电流内环、功率外环、直流电压外环分别设计为Ⅰ型环节、一阶环节和Ⅱ型环节，使得控制系统具有良好的稳态和动态性能，但不易获得合适的阻尼比。文献[8-10]采用智能算法对简化整定模型的PI参数进行优化，但仅局限于整流侧定电流控制。

针对上述工作的不足，文中提出一种基于最优控制策略的外环参数整定方法：建立解耦后的外环参数整定模型；基于时间乘绝对误差积分（integral of time multiplied by the absolute value of error，ITAE）准则构造PI参数优化的性能泛函；针对以上最优控制的特点，采用遗传算法（genetic algorithm，GA）进行迭代求解，从而获得控制器的优化参数。

1 VSC模型

1.1 VSC数学模型概述

三相VSC的主电路结构如图1所示，其中，usa、usb、usc分别为交流母线侧三相电压；isa、isb、isc分别为交流母线侧三相电流；R、L分别为换流变压器的电阻与电抗；uca、ucb、ucc分别为换流器侧三相电压；idc、iL分别为换流器流出电流以及直流线路电流；C为直流线路电容；Udc为直流线路电压。

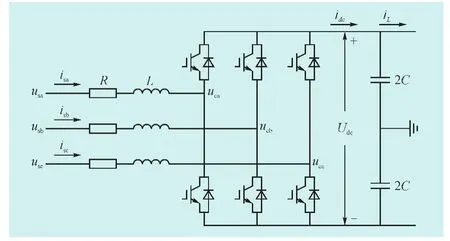
图1三相VSC拓扑结构Fig.1 Topology of three-phase VSC

abc坐标系下VSC的时域数学模型为式（1）～式（2）[11]

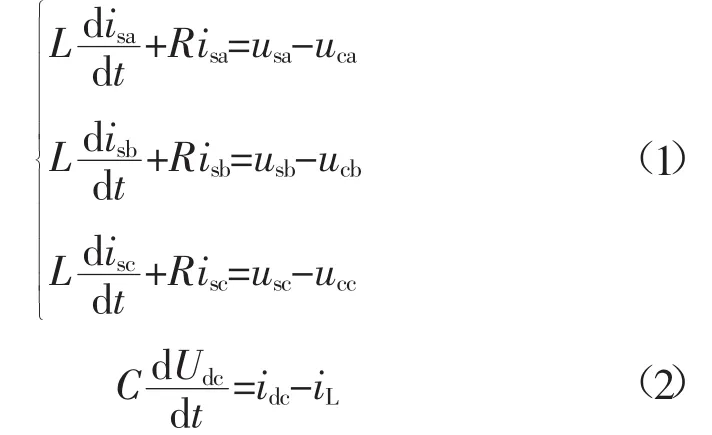
通过Park变换（如式（3）所示），将式（1）转换到dq同步旋转坐标系下，可得到式（4）。

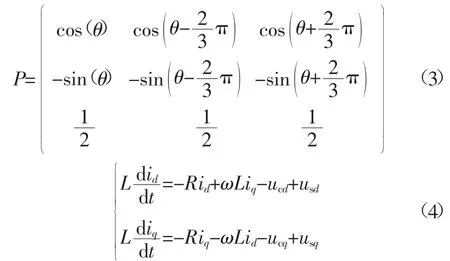
若dq同步旋转坐标系的d轴与电网电压矢量重合，则uq为0。交流系统注入VSC的有功和无功功率分别为

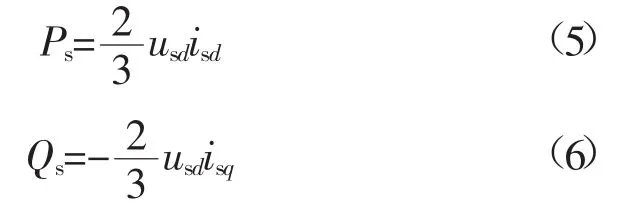
图2为一端VSC直接电流控制基本原理示意图。其中A参考为有功功率类控制量，B参考为无功功率类控制量。有功功率类控制主要包括定有功功率控制、定直流电压控制；定无功功率类控制主要包括定无功功率控制、定交流电压控制。

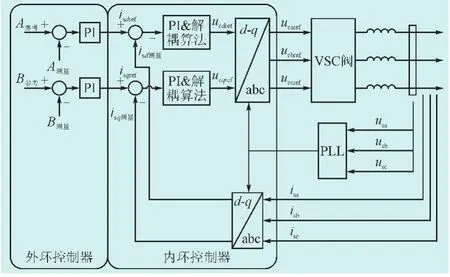
图2 一端VSC直接电流控制基本原理示意图Fig.2 Diagram of direct current control fundamentals on one sided VSC

1.2 VSC控制器PI参数整定模型

1.2.1 有功功率类控制器PI参数整定模型

1）定直流电压控制

若整流侧不向逆变侧传输有功功率，则有iL=0，由式（2）可知

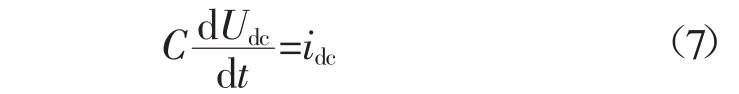
若换流器和直流线路的有功功率损耗为0，则

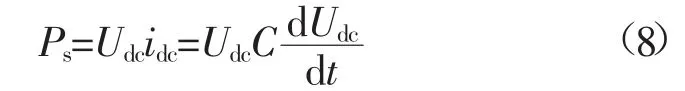
图3为定直流电压控制器的PI参数整定模型，其中，PI控制环节G0（s）=KP+Ki/s，等效电流内环G1（s）= 1/（1+3Tss）[12-15]，等效直流线路方程G2（s）=1/sC，考虑到直流侧和交流侧有功功率的平衡G3（s）=3usd/2Udc，量测环节产生的时延G4（s）=1/（1+Tss），isdmax和isdmin分别为isdref的上下限值，Ts为PWM开关周期。

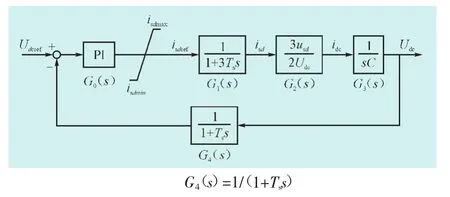
图3 定直流电压控制器整定模型Fig.3 Diagram of DC voltage control scheme

2）定有功功率控制

图4为定有功功率控制器的PI参数整定模型。

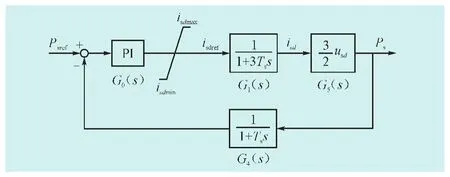
图4 定有功功率控制器整定模型Fig.4 Diagram of active power control scheme

1.2.2 无功功率类控制器PI参数整定模型

1）定无功功率控制

图5为定无功功率控制器的PI参数整定模型。定无功功率控制器的PI参数本身为负，与式（6）中的负号抵消，故图5中的PI参数为正。其中，isqmax和isqmin分别为isqref的上下限值。

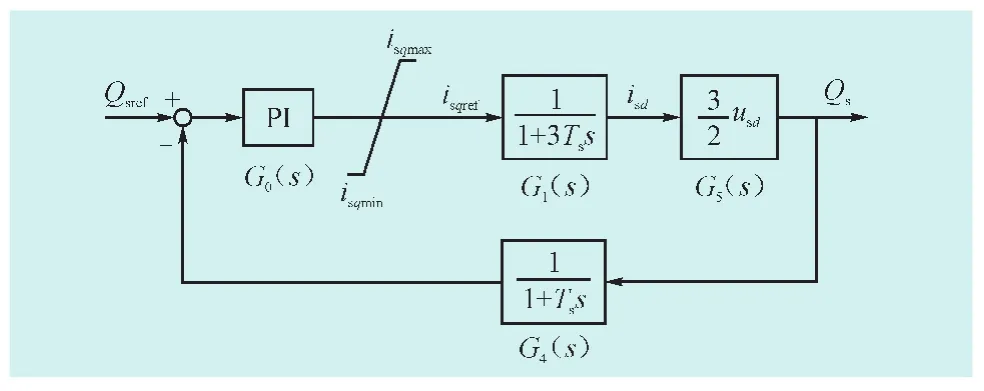
图5 定无功功率控制器整定模型Fig.5 Diagram of reactive power control scheme

2）定交流电压控制

图6为定交流电压控制器的PI参数整定模型。忽略交流系统的电阻，其中，X为交流系统电抗，Ed电源电压。

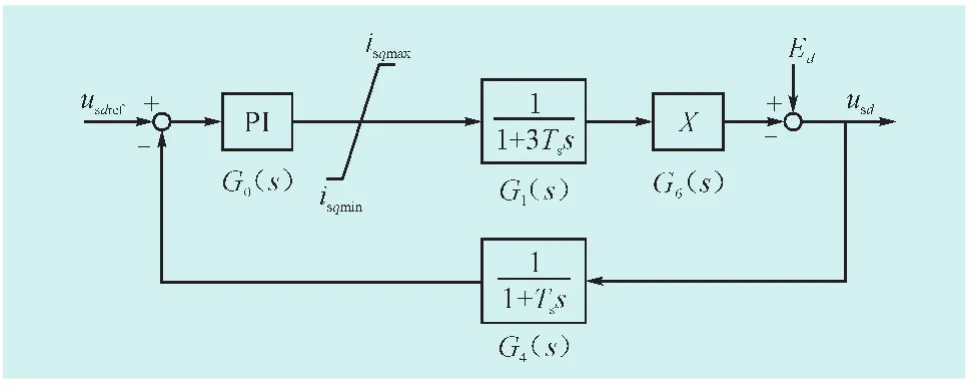
图6 定交流电压控制器整定模型Fig.6 Diagram of AC voltage control scheme

2 参数优化

2.1 文中方法的动机

时间乘绝对误差积分（integral time absolute error，ITAE）指标是常用的评估控制系统动态响应的指标之一，它不仅综合考虑稳态误差与调节时间，且可使系统动态响应过程快速、平稳、超调量小。基于以上考虑，文中基于ITAE指标来构造PI参数优化的性能泛函。

2.2 具体模型

一般的，基于ITAE指标的最优控制性能泛函为

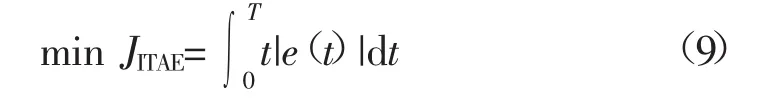
式中：积分上限T为系统响应达到稳定的时间；e（t）为动态调整过程中参考值与实际输出值之间的偏差。

考虑到VSC-HVDC控制系统中有4个外环控制器，则基于ITAE指标构建VSC控制器中PI参数优化的最优控制模型为

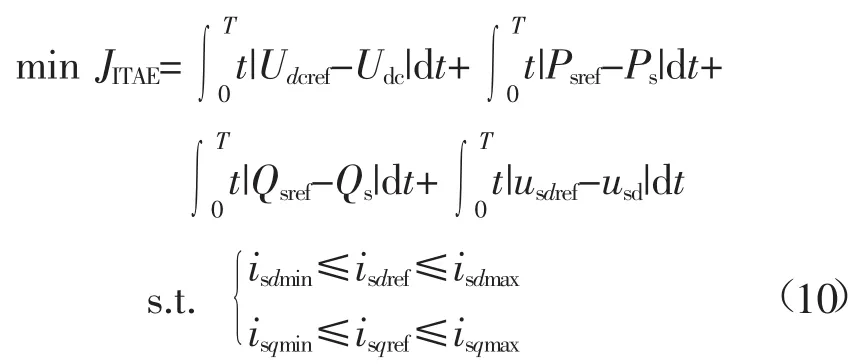
式中：Udcref、Psref、Qsref和usdref为定值，但难以获得Udc、Ps、Qs、usd与外环PI参数间的解析表达式，因此不能通过传统优化算法获得模型的最优解。

2.3 求解方法

遗传算法是模仿自然界进化机制发展起来具有全局搜索能力的高效、并行优化方法。以下利用遗传算法求解模型（10），具体步骤如下：

1）编码和初始种群的产生。设置遗传算法的个体数目N、最大迭代次数M、选择算子、交叉算子和变异算子，PI控制器优化控制变量（KP、Ki）的二进制取值范围对控制变量进行编码。随机生成N个初始个体，设定当前迭代次数n=1。

2）适应度值评价检测。针对式（10）所示的目标函数，对种群中的个体进行适应度值的计算。

3）选择、交叉和变异。

4）重新插入子代。

5）若迭代次数达到M或精度满足收敛要求，则停止搜索，输出最佳结果；否则，转步骤2）。

遗传算法的迭代在matlab编程中实现，目标函数值的计算通过在matlab/simulink中搭建模型的方式实现。在simulink中对整定模型进行仿真时，参考值均为阶跃函数；遗传算法保证了能够在PI参数的取值范围内获得最优解，在S imulink中对整定模型进行仿真既可节约计算所需时间又保证了一定的准确度。完整运算流程如图7所示。

图7 VSC-HVDC控制系统PI参数计算流程图Fig.7 Flow chart of the process for determ ining the PI compensator parameters for VSC-HVDC control system

3 仿真分析

针对图3—图6所示的整定模型，利用试凑法拟定控制器参数初值，给出与文中基于ITAE指标的VSC控制器PI参数优化结果，将优化前后被控制量波形在完整VSC模型中进行仿真对比分析。VSC的直流电压为±200 kV；换流变压器变比为230 kV/ 66 kV；额定容量为100 MV·A；直流线路电容C为125μF；交流系统电抗X为26Ω。采用以下4种控制方案，优化前后参数值如表1所示。仿真拓扑结构图如图8所示。

1）定有功功率/交流电压控制

采用定有功功率/交流电压控制的VSC，其响应曲线如图9和图10所示。0.5 s时有功功率参考值由-0.5 pu上升到0.5 pu，1.5 s时有功功率参考值由0.5 pu下降到-0.5 pu。1.0 s时交流电压参考值由0.9 pu上升到1.1 pu，2.0 s时交流电压参考值由1.1 pu下降到0.9 pu。图中，红色曲线为参考值，绿色曲线为优化前的响应曲线，蓝色曲线为优化后的响应曲线。

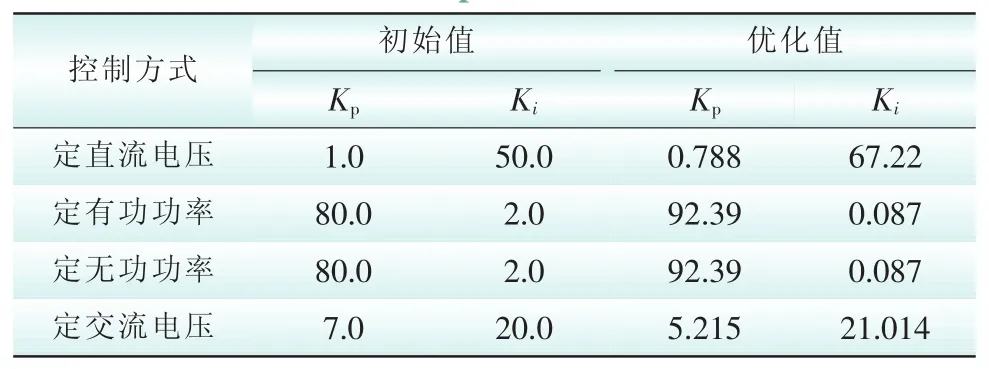
表1 优化前后PI控制器参数Tab.1 PI com pensator parameters before and after optim ization

图8两端VSC-HVDC系统接线Fig.8 Schematic diagram of a back-to-back VSC-HVDC system

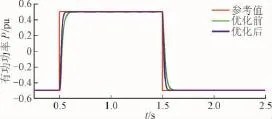
图9 有功功率响应曲线Fig.9 Response of active power

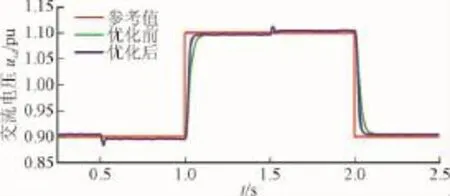
图10 交流电压响应曲线Fig.10 Response of AC voltage

与优化前相比，文中提出最优控制方法提高了有功功率和交流电压的响应速度。有功功率基本不受交流电压参考值变化的影响，交流电压却受有功功率参考值的影响；交流电压波动主要取决于系统潮流中的无功分量，但同样受有功功率变化的影响。

2）定直流电压/交流电压控制

采用定直流电压/交流电压控制的VSC，其响应曲线如图11和图12所示。0.5 s时直流电压参考值由0.875 pu上升到1.125 pu；1.5 s时直流电压参考值由1.125 pu下降到0.875 pu；1.0 s时交流电压参考值由0.9 pu上升到1.1 pu；2.0 s时交流电压参考值由1.1 pu下降到0.9 pu。图中，红色曲线为参考值，绿色曲线为优化前的响应曲线，蓝色曲线为优化后的响应曲线。

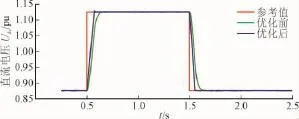
图11 直流电压响应曲线Fig.11 Response of DC voltage

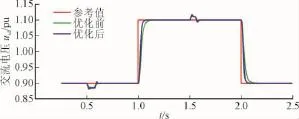
图12 交流电压响应曲线Fig.12 Response of AC voltage

与优化前相比，文中提出的最优控制方法提高了直流电压和交流电压的响应速度。直流电压基本不受交流电压参考值变化的影响，交流电压却受直流电压参考值的影响，直流电压参考值的改变影响了有功功率的传输。

3）定有功功率/无功功率控制

采用定有功功率/无功功率控制的VSC，其响应曲线如图13和图14所示。0.5 s时有功功率参考值由-0.6 pu上升到0.6 pu；1.5 s时有功功率参考值由0.6 pu下降到-0.6 pu；1.0 s时无功功率参考值由-0.8 pu上升到0.8 pu；2.0 s时无功功率参考值由0.8 pu下降到-0.8 pu。图中，红色曲线为参考值，绿色曲线为优化前的响应曲线，蓝色曲线为优化后的响应曲线。

图13 有功功率响应曲线Fig.13 Response of active power

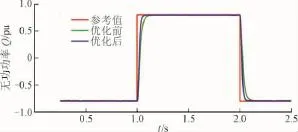
图14 无功功率响应曲线Fig.14 Response of reactive power

与优化前相比，文中提出的最优控制方法提高了有功功率和无功功率的响应速度，有功功率和无功功率能够实现完全解耦控制。

4）定直流电压/无功功率控制

采用定直流电压/无功功率控制的VSC，其响应曲线如图15和图16所示。0.5 s时直流电压参考值由0.875 pu上升到1.125 pu；1.5 s时直流电压参考值由1.125 pu下降到0.875 pu；1.0 s时无功功率参考值由-0.8 pu上升到0.8 pu；2.0 s时无功功率参考值由0.8 pu下降到-0.8 pu。图中，红色曲线为参考值，绿色曲线为优化前的响应曲线，蓝色曲线为优化后的响应曲线。

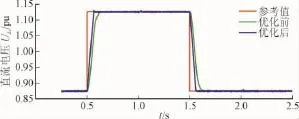
图15 直流电压响应曲线Fig.15 Response of DC voltage

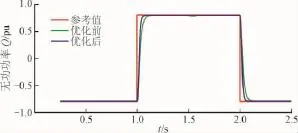
图16 无功功率响应曲线Fig.16 Response of reactive power

与优化前相比，文中提出的最优控制方法提高了直流电压和无功功率的响应速度，直流电压和无功功率能够实现完全解耦控制。无功功率的变化不会影响直流电压，直流电压的变化也不会影响无功功率，却会影响交流电压，从侧面反映了有功功率和无功功率可以实现解耦控制，交流电压却同时受有功功率和无功功率变化的影响。

4 结语

传统VSC控制器中的PI参数选取需要较高的经验和技巧，不易获得满意效果。文中提出一种基于时间乘绝对误差积分指标的最优控制策略用于对VSC控制器中的PI参数进行优化。针对此模型的特点，论文选用遗传算法进行求解，在PSCAD中对完整VSC模型进行仿真计算，验证了文中所提方法可使得VSC的动态响应过程快速、平稳、超调量小。

[1]杨方，张义斌，葛旭波，等.德国海上风电VSC-HVDC技术分析[J].电网与清洁能源，2012（10）:63-68，73. YANG Fang，ZHANG Yibin，GE Xubo，et al.Technical analysis of VSC-HVDC in germany’offshore wind power[J].Power System and Clean Energy，2012（10）:63-68，73（in Chinese）.

[2]李广凯，江政昕，赵昕，等.电压源换流器高压直流输电的特点与前景[J].南方电网技术，2011（5）：13-17. LIGuangkai，JIANG Zhengxin，ZHAO Xin，et al.The characteristics and prospect of VSC-HVDC power transmission[J].Southern Power System Technology，2011（5）: 13-17（in Chinese）.

[3]张静.VSC-HVDC控制策略研究[D].杭州：浙江大学，2009.

[4]郭丽，赵成勇，李广凯，等.VSC-HVDC在电网黑启动时负荷恢复阶段提高系统频率稳定性研究[J].华北电力大学学报（自然科学版），2007（5）:22-26，31. GUO Li，ZHAO Chengyong，LIGuangkai，et al.VSCHVDC for enhancing power system frequency stability in the load restoration stage of black start[J].Journal of North China Electric Power University，2007（5）：22-26，31（in Chinese）.

[5]杨汾艳，徐政，张静.直流输电比例-积分控制器的参数优化[J].电网技术，2006（11）:15-20. YANG Fenyan，XU Zheng，ZHANG Jing.Study on parameter optimization of HVDC PI controllers[J].Power System Technology，2006（11）：15-20（in Chinese）.

[6]阮立煜.基于粒子群算法的VSC-HVDC控制参数优化[J].浙江电力，2015（1）：9-13. RUAN Liyu.Optimization of VSC-HVDC control parameters based on particle swarm optimization[J].Zhejiang Electric Power，2015（1）：9-13（in Chinese）.

[7]杨晓楠，陈红坤，缪芸，等.一种VSC-HVDC控制系统的PI参数整定方法[J].现代电力，2015（4）：68-73. YANG Xiaonan，CHEN Hongkun，Miao Yun，et al.A method of PI parameters tuning for VSC-HVDC control system[J].Modern Electric Power，2015（4）：68-73（in Chinese）.

[8]王振浩，郭顺楠，黄延青.改进ACO算法优化的PI控制器在直流输电控制中的应用[J].电工电能新技术，2015（5）：70-75. WANG Zhenhao，GUO Shunnan，HUANG Yanqing.Application of improved ACO algorithm optimized PI controller in control of HVDC[J].Advanced Technology of Electrical Engineering and Energy，2015（5）：70-75（in Chinese）.

[9]周孝法，陈陈，宋正强，等.基于改进PSO算法的HVDC PI控制器优化设计[J].高电压技术，2009（2）：408-414. ZHOU Xiaofa，CHEN Chen，SONG Zhengqiang，et al. Optimal design for HVDC PI controllers based on improved PSO algorithm[J].High Voltage Engineering，2009（2）：408-414（in Chinese）.

[10]胡江，魏星.基于自适应粒子群算法的直流输电PI控制器参数优化[J].电网技术，2008（S2）：71-74. HU Jiang，WEI Xing.Parameter optimization of HVDC technology PI controller based on adaptive particle swarm optimization[J].Power System Technology，2008（S2）：71-74（in Chinese）.

[11]GUAN M，XU Z.Modeling and control of amodularmultilevel converter-based HVDC system under unbalanced grid conditions[J].IEEE Transactions on Power Electronics，2012，27（12）：4858-4867.

[12]WANG L，ERTUGRUL N.Selection of PI compensator parameters for VSC-HVDC system using decoupled control strat-egy[C]//Universities Power Engineering Conference（AUPEC），2010 20th Australasian.IEEE，2010:1-7.

[13]BAJRACHARYA C，MOLINAS M，SUUL J A，et al. Understanding of tuning techniques of converter controllers for VSC-HVDC[C]//Nordic Workshop on Power and Industrial Electronics（NORPIE/2008），June 9-11，2008，Espoo，Fin-land.HelsinkiUniversity of Technology，2008.

[14]陈谦，李冲，金宇清，等.基于并网型VSC解耦模型的控制器参数优化[J].高电压技术，2014（8）：2478-2484. CHEN Qian，LIChong，JIN Yuqing，et al.Optimization of grid-connected VSC controller by decouplingmodels[J]. High Voltage Engineering，2014（8）：2478-2484（in Chinese）.

[15]SUUL JA，MOLINASM，NORUM L，etal.Tuning of control loops for gridconnected voltage source converters[C]// Power and Energy Conference，2008.PECon 2008.IEEE 2nd International.IEEE，2008:797-802.

Control System PIParameter Optim ization Based on Genetic Algorithm for VSC-HVDC

CUIJingsi1，GAO Kai2，HAN Zijiao2，ZHANG Yanjun2，CHEN Yanbo3，MA Jin4
（1.State Grid Tianjin Dongli Power Company，Tianjin 300300，China；2.State Grid Liaoning Electric Power Company，Shengyang 110006，Liaoning，China；3.North China Electric Power University，State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources，Beijing 102206，China；4.School of Electrical and Information Engineering，The University of Sydney，Sydney NSW，2006，Australia）

This paper proposes an approach to the optimization of the parameters of the proportional-integral（PI）compensators in the various external loops of a VSC-HVDC transmission system using a direct current control strategy.Setting models of parameters in external loops are established.The optimized parameters are calculated using genetic algorithm based on the PI controllers’initial values under ITAE（integral of time multiplied by the absolute value of error）criteria. The validity of the optimization method is verified in a detailed electromagnetic transient（EMT）model of the VSC-HVDCmodel in PSCAD.The simulation results show that the proposed method in this paper has good effects and high computational efficiency.

VSC；PI controller；setting model；genetic algorithm

2016-10-23。

崔静思（1992—），女，硕士，主要研究方向为柔性直流输电。

（编辑 张晓娟）

2014年国家电网公司科技项目“柔性环网控制器关键技术研究及示范应用”（2014GW-05）。

Project Supported by the Science and Technology Project of SGCC 2014“Research and Application on Key Technology of Flexible Looped Network Controller”（2014GW-05）.

1674-3814（2017）02-0026-06

TM71

A