自适应网格密度改进粒子群算法在多目标无功优化中的应用

徐基光

（国网安徽省电力公司芜湖县供电公司，安徽芜湖 241100）

自适应网格密度改进粒子群算法在多目标无功优化中的应用

徐基光

（国网安徽省电力公司芜湖县供电公司，安徽芜湖 241100）

粒子群算法因其具有收敛速度快和参数调节灵活等优点而被广泛应用于多目标无功优化领域，然而粒子群算法快速收敛特征极易收敛到局部最优解。提出了一种基于自适应网格密度的改进多目标粒子群算法（AG-MOPSO）。通过自适应网格确定粒子的个体密度，并利用该信息对外部档案进行维护，进一步利用自适应网格估算非劣解的密度信息，采用轮盘赌法确定全局最优解，提升了种群多样性。以网损和电压偏移为目标，采用IEEE30节点系统进行算例分析，验证了改进AG-MOPSO算法在寻优过程中的高效性。

多目标；无功优化；粒子群；自适应网格；Pareto最优

无功优化作为电力系统的关键技术，不仅影响电压质量，还对电力系统运行的稳定性、安全性和经济性起着至关重要的作用。随着电力系统规模的不断扩大，无功优化涉及目标呈现多样化，逐渐发展成为综合考虑电压质量、安全裕度和经济性等多种运行指标的多目标优化问题[1-3]。传统方法往往通过设定偏好参数将多目标无功优化问题转化为单目标优化问题求解，然而由于无功优化目标的差异，偏好参数难以确定，使得权衡问题日益突出。

多目标进化算法的出现为此类问题提供了新的解决思路，这些方法能够搜索得到Pareto最优解集，可避免决策者预先设定偏好参数，因此在无功优化领域得到了广泛应用。其中多目标粒子群优化算法（multi-objective particle swarm optimization，PSO，MOPSO）因其收敛速度快、参数调节灵活、一次运行可同时得到多个解、且能有效逼近不连续的Pareto前沿，被广泛认为是求解多目标优化问题最具有潜力的方法之一[4]。然而粒子群的快速收敛特征使得MOPSO算法极易收敛到伪Pareto前沿，很多学者针对这一问题提出了改进措施，主要集中在以下3点：如何维护存储Pareto最优解集的档案；如何选择全局最优解gbest和个体最优解pbest；如何平衡进化过程中粒子的“开采”和“开发”能力。

本文将根据多目标无功优化问题和MOPSO算法的特征，采用自适应网格密度估计方法对外部档案进行维护，并将非劣解的密度信息与轮盘赌法结合，给出了全局最优解的选择策略。以网损和电压偏移为目标，采用IEEE30节点系统进行算例分析，与其他粒子群算法比较，验证了改进算法的优势。

1 多目标无功优化数学模型

多目标优化问题是指2个或2个以上目标需要同时优化的问题，由n变量参数、k个目标函数和m个约束条件组成的最优化问题可表示为

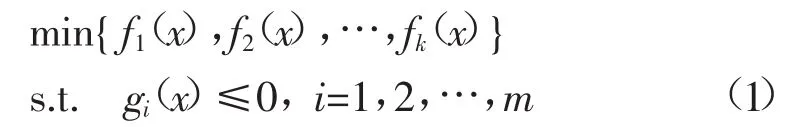
式中：x∈Rn；fi（x）为目标函数；gi（x）为m个不等式约束函数。本文以有功损耗和电压偏差作为多目标：

式中：fLoss为系统网损；fVD为电压偏移；N系统节点数；NL为输电线路集合；NG为发电机数；NT为变压器可调分接头数；NC为并联电容器数；gij为节点i与j之间线路的电导；θij为节点i与j之间的电压相角差；NPQ为PQ母线集合；U为节点i的电压基准值；PGi和PLi分别为节点i发电机和负荷的有功功率；QGi、QLi、QCi分别为节点i处发电机、负荷无功功率和电容补偿器的无功功率注入量；NPV为PV母线集合；Gij和Bij分别为导纳矩阵第i行、第j列元素的实部和虚部；UGimin、UGimax、QCimin、QCimax、Timin、Timax、QGimin、QGimax、Uimin和Uimax分别为相应变量的上限和下限值。

2 基于自适应网格密度的多目标粒子群优化算法

2.1 多目标粒子群优化算法

2.1.1 Pareto最优

一般情况下，多个目标之间相互制约，其解往往不局限于单一解，可能存在多个解，通常用Pareto最优集表示。

定义1（Pareto占优）设F：Rn→Rm，xA，xB∈Ω⊆Rn，称xA占优xB当且仅当：∀i∈{1，2，…，m}，fi（xA）≤fi（xB）且∧∃j∈{1，2，…，m}，fj（xA）＜fj（xB），记作xA≻xB。

定义2（Pareto最优解）个体x*∈Ω称为Pareto最优解（或非支配解），当且仅当：

所有Pareto最优解组成的集合定义为Pareto最优解集P*，将该解集中所有Pareto最优解对应的目标矢量组成的曲面称为Pareto前沿面PF*：

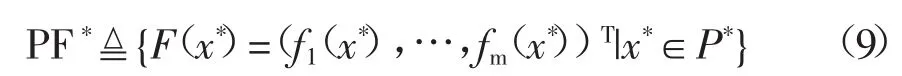
2.1.2 粒子群优化算法

在经典PSO算法[5-7]中，假设每个粒子表示为n维搜索空间中的一点，第i个粒子位置表示为xi=（x，x，…，x），该粒子速度为，粒子i所得到的个体最优解表示为），pgd表示为全局最优解。在每次迭代中，粒子i的位置和速度通过如下公式进行更新：

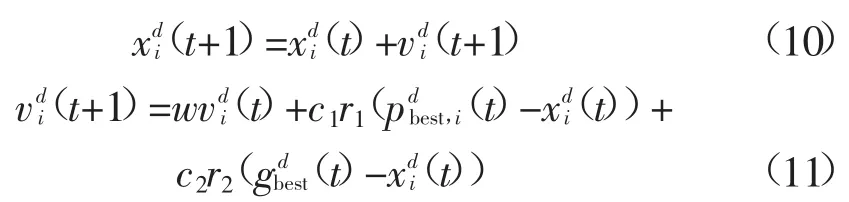
式中：t为迭代次数；c1、c2为加速因子；r1、r2为0～1之间的随机数；w为惯性权重；x为第i个粒子个体的第d维分量；pest，i为第i个粒子个体最优解的第d维分量；g为群体最优解的第d维分量。

当PSO算法从单目标问题扩展到多目标问题而形成MOPSO算法时，新的技术问题随之出现，全局最优解不是唯一确定的，借助外部档案存放Pareto最优解，因此Pareto最优解维护，全局最优解选择和种群多样性增加等问题成为影响MOPSO算法性能好坏的关键。本文在此基础上提出了基于自适应网格密度的多目标粒子群优化算法（AG-MOPSO），通过自适应网格密度对粒子拥挤度进行估计，并利用密度信息对外部档案进行维护，进一步结合轮盘赌法对全局最优解进行了选择。

2.2 AG-MOPSO算法的关键算子

2.2.1 自适应网格密度估计

首先建立k维目标空间的自适应网格，将目标空间分为D1×D2×…×Dk网格，其中第i个目标网格模长di按照式（12）计算：

外部档案成员个数M会自动随外部档案中的非占优解的个数变化而变化，因此目标空间的网格数也会随之自适应变化，无须用户依赖先验知识进行设定。非占优解在自适应网格空间的位置pi由式（13）确定：

式中：mod（x，y）为x/y后的整数部分。根据式（13）可以计算出每个网格内包含的非占优解个数，将一个网格内非占优解的个数作为粒子的分布密度，如图1所示。

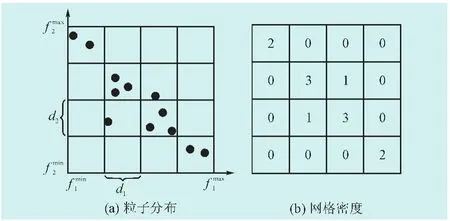
图1 种群密度估计Fig.1 Population density estimation

2.2.2 外部档案的维护策略

在采用外部档案存储Pareto最优解集时，外部档案的存储于维护显得尤为重要，为防止外部档案过度膨胀，增加计算复杂度，需对外部档案的最大存储容量进行限制，设最大成员数为Mmax，外部待更新的档案为A，如果进化算法获得一个新解S，具体维护算法如下所示。

算法1 当M＜Mmax

Step1.如果A中存在一个成员占优S，则直接返回A；

Step2.如果S占优A中某一成员ai，则返回A=A/ {ai}∪{S}；

Step3.如果S与A中任一成员互不占优，则返回A=A∪{S}。

算法2 当M≥Mmax

Step1.生成新的集合H=A∪{P}，根据式（12）、式（13）进行自适应网格划分，评估成员个体密度；

Step2.查找H中具有最大个体密度的成员，组成集合H′；

Step3.随机选取H′max，i删除，则返回A=H/{H′max，i}∪{S}。

2.2.3 全局最优解的选择策略

由式（10）和式（11）可知，粒子运行轨迹受个体最优解和全局最优解的影响，大多数MOPSO算法仅保存一个个体最优解，其更新方法如算法3所示。

算法3 个体最优解选择

Step1.当粒子发现的新解P′占优时，采用新解作为个体最优解，即Pbest=P′；

Step2.当旧解占优时，Pbest保存不变；

Step3.当P′与旧解互为Pareto最优解时，随机选取一个解作为Pbest。

然而全局最优解是一组Pareto最优解集，如果没有有效的选择策略，则无法有效地控制算法的开采和开发过程，本文采用自适应网格密度和轮盘赌法进行全局最优解的选择，可使每一代的全局最优解不完全相同，具体算法如算法4所示。

算法4 全局最优解选择Step1.利用自适应网格法评估粒子的个体密度；Step2.将个体密度等级为Z的粒子统一放入集合HZ中；

Step3.将个体密度等级除以所有个体密度等级之和，采用轮盘赌法来选择个体密度等级；

Step4.在相应个体密度等级集合中随机选取粒子作为全局最优解。

2.3 基于AG-MOPSO的多目标无功优化

用于解决多目标优化问题的自适应网格密度粒子群优化算法（AG-MOPSO）描述如下：

1）输入电网运行数据，初始化AG-MOPSO算法参数。

2）进行潮流计算，计算各子目标函数值，更新粒子个体最优解Pbest。

3）判断个体最优解是否为Pareto最优解，若是则将其放入外部档案，并返回粒子存储个数M。

4）进入循环，t=t+1，根据算法4选取全局最优解Gbest，根据式（10）、式（11）更新粒子位置，修正越界，并对控制变量离散化，进行潮流计算，计算适应度函数值，根据算法1）—3）更新信息。

5）判断算法循环终止条件，若未达到最大进化迭代数，则转至步骤4），否则输出结果。

3 实验仿真

本文对IEEE30节点系统进行测试，该系统具有41条支路，6个发电机节点（节点1、2、5、8、11、13），22个负荷节点，4条可调变压器支路（T6-9、T6-10、T4-12、T27-28），选取2个节点（节点10、节点24）作为无功补偿点。无功注入功率调节步长为0.01，变压器调整补充为0.012 5。标幺值基准电压为220 V，基准功率为100MV·A，IEEE30系统参数参见文献[8-11]，其总负荷Pload=2.843MW，Qload=1.262 var，设发电机端电压和变压器的变比均为1.0，在初始条件下，通过潮流计算得到，Ploss=0.059 71 MW。CA-MOPSO算法中相关参数选取分别为种群规模pop=100，最大迭代次数300，c1=c2=2.05，w=0.8。

粒子的变量对应于发电机端电压，可调变压器变比，并联电容器无功补偿量，具体表述为

式中：Vij（j=1，…，NG）为每台发电机的端电压，属于连续变量；Tij（j=1，…，NT）为可调变压器变比，为离散变量；Qij（j=1，…，NC）为各节点无功补偿量，为离散变量。因此在优化过程中需对控制变量中进行如下离散化：

式中：ΔT为变压器分接头的调节步长；ΔQj第j个无功补偿的调节步长。

针对寻优过程中出现的越界情况，采取惩罚措施，适应度函数计算公式为

算法独立运算30次，选取其最佳一次运行结果，AG-MOPSO获得的Pareto前沿如图2所示，其Pareto边界点如表1所示。

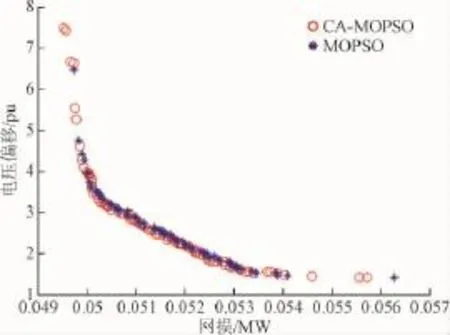
图2 IEEE30节点系统的Pareto最优解集Fig.2 Pareto optimal solution set of IEEE 30 bus system

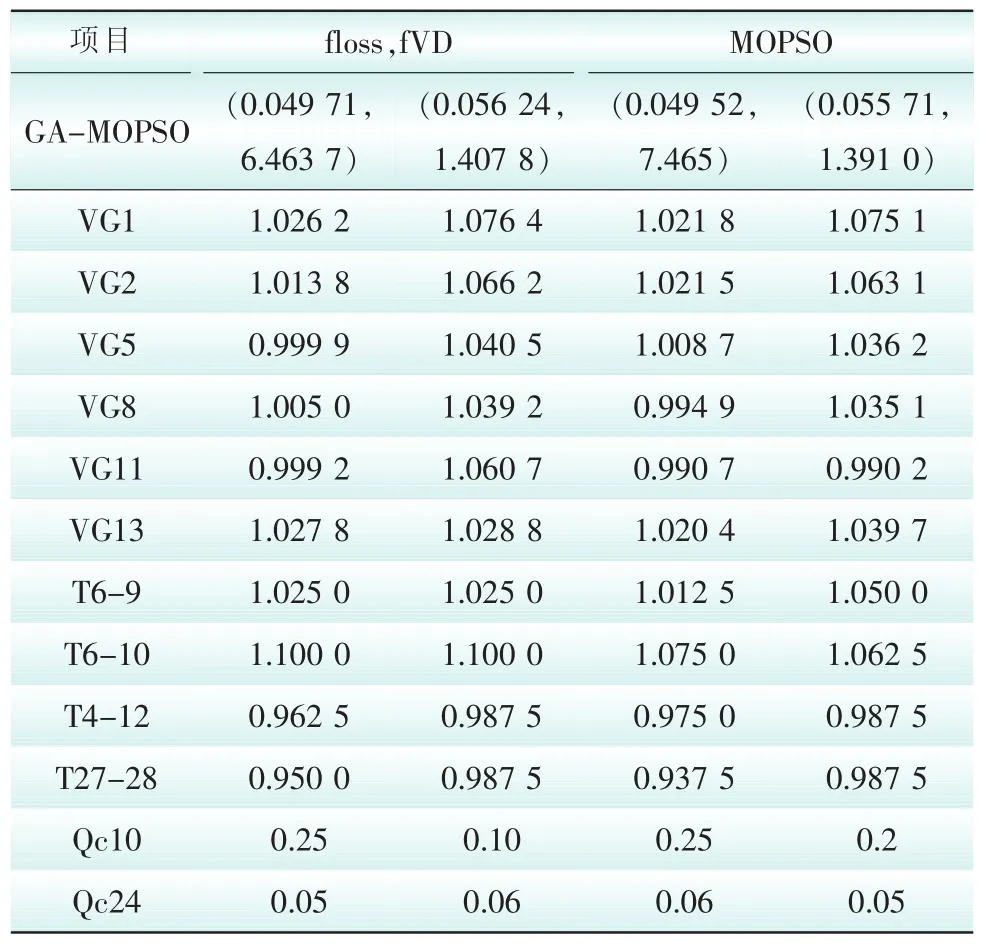
表1 IEEE30节点系统的Pareto边界点Tab.1 Pareto boundary solution of IEEE 30bus system pu

由图2可知，CA-MOPSO获得的Pareto解集在目标空间沿着一定的曲线展开，所含候选解数量较MOPSO多，且分布广泛，由表1可得CA-MOPSO的边界点（0.055 71，1.391 0）Pareto占优MOPSO（0.056 24，1.407 8），证实了该CA-MOPSO算法的有效性。若仅以网损最小为单目标函数，CA-MOPSO优化后有功网损为0.049 52，损耗降低了17.07%，优于MOPSO得到的最小网损。将该结果与仅考虑单目标优化的结果比较，AFPSO算法[8]降损11.939 2%、PSO-cf算法[8]降损1.785 3%，CLPSO算法[9]降损7.055 7%，进一步显示了CA-MOPSO算法的优势。

4 结语

粒子群算法具有参数少、收敛速度快等特点，在电力系统无功优化中得到了广泛应用。然而算法早熟收敛等问题限制了其发展。本文针对多目标无功优化问题，提出利用自适应网格评估粒子密度，并据此进行档案维护和最优解的选取，通过测试系统分析，证实了该算法的有效可行性，该方法可推广应用于其他多目标优化问题的求解。

[1]张珂，吕林，孙宇乐.基于隶属度时段划分的配电网动态重构[J].电力系统保护与控制，2016，44（3）：51-57. ZHANG Ke，LÜLin，SUN Yule.Dynamic reconfiguration of distribution network based on membership partition of time intervals[J].Power System Protection and Control，2016，44（3）：51-57（in Chinese）.

[2]潘超，焦薇羽，孟涛，等.基于混合智能粒子群算法的广义电源主动配电网优化配置[J].电力系统保护与控制，2016，44（7）：69-75. PAN Chao，JIAO Weiyu，MENG Tao，et al.Optimal allocation of generalized power sources in active distribution network based on hybrid intelligent particle swarm optimization algorithm[J].Power System Protection and Control，2016，44（7）：69-75（in Chinese）.

[3]刘力卿，米增强，袁贺，等.考虑风电的无功辅助服务市场多目标出清[J].华北电力大学学报，2015，42（3）：22-30. LIU Liqing，MI Zengqiang，YUAN He，et al.Multiobjective clearing of reactive power auxiliary servicemarket considering wind power[J].Journal of North China Electric Power University，2015，42（3）：22-30（in Chinese）.

[4]胡殿刚，秦睿，黄亭，等.基于免疫记忆粒子群优化算法的风火联合系统的多目标优化调度[J].高压电器，2015，51（6）：20-26. HU Diangang，QIN Rui，HUANG Ting，etal.Wind power integrated with thermal system multi-objective optimal dispatch based on immune memory particle swarm optimization algorithm[J].High Voltage Apparatus，2015，51（6）：20-26（in Chinese）.

[5]张力月，张江滨.基于改进PSO的独立风光系统混合储能容量优化研究[J].电力与能源，2016，37（4）：471-475. ZHANG Liyue，ZHANG Jiangbin.Optimization research on the hybrid energy storage capacity of stand-alonewind/ PV micro-grid based on improved PSO[J].Power& Energy，2016，37（4）：471-475（in Chinese）.

[6]蓝文昊，郑益慧，李立学，等.基于萤火虫-粒子群混合算法的接地网分区域故障诊断方法[J].电瓷避雷器，2015，4（3）：92-99. LAN Wenhao，ZHENG Yihui，LI Lixue，et al.Regional fault diagnosis method for grouding grids based on glowworm-particle swarm hybrid optimization algorithm[J]. Insulators and Surge Arresters，2015，4（3）：92-99（in Chinese）.

[7]马立新，王继银，项庆，等.三目标混合骨干粒子群算法的电力系统无功优化[J].电力科学与工程，2015，31（11）：18-25 MA Lixin，WANG Jiyin，XIANG Qing，et al.Threeobjective hybrid bare-bones Particle Swarm Optimization for reactive power optimization[J].Electric Power Science and Engineering，2015，31（11）：18-25（in Chinese）.

[8]贾逸伦，龚庆武，雷杨，等.基于灰色关联与量子粒子群寻优的光伏短期预测[J].电网与清洁能源，2016，32（2）：109-115. JIA Yilun，GONG Qingwu，LEIYang，et al.Photovoltaic power short-term prediction based on grey related analysis and QPSO-SVM[J].Power System and Clean Energy，2016，32（2）：109-115（in Chinese）.

[9]吕锋，张健.基于PSO的SVC附加阻尼控制器参数优化设计[J].电力电容器与无功补偿，2016，37（2）：11-15. LÜFeng，ZHANG Jian.Parameter optimization design of PSO-based SVC additional damping controller[J].Power Capacitor&Reactive Power Compensation，2016，37（2）：11-15（in Chinese）.

[10]陈梓铭.基于万有引力搜索算法的电力系统电压无功控制策略研究[J].江苏电机工程，2016，35（1）：61-65. CHEN Ziming.Gravitational search algorithm based voltage reactive power control strategy research[J].Jiangsu Electrical Engineering，2016，35（1）：61-65（in Chinese）.

[11]张铁峰，李佳，顾建炜.基于IEC61850的配电电压无功控制全模型架构研究[J].电力信息与通信技术，2016，14（4）：134-139. ZHANG Tiefeng，LI Jian，GU Jianwei.Research on the full model architecture of distribution voltage/var control based on IEC61850[J].Electric Power ICT，2016，14（4）：134-139（in Chinese）.

Im proved Particle Swarm Optim ization Algorithm Based on Adaptive Grid Density and Its App lication on M ulti-Objective Reactive Power Optim ization

XU Jiguang
（Wuhu Power Supply Company，State Grid Anhui Electric Power Supply Company，Wuhu 241100，Anhui，China）

Particle swarm optimization（PSO）algorithm is widely applied to multi-objective reactive power optimization due to its fast convergence，flexible parameter adjustment and so on.However，the fast convergence characteristic of particle swarm algorithm is extremely easy to converge to local optimal solutions.To solve the problem，based on adaptive grid density，an improved multi-objective particle swarm algorithm（AG-MOPSO）is proposed in this paper.Individual density of each particle is determined bymeans of adaptivemesh，and its information is used to maintain the external file.The non inferior solution density information is estimated and combined with the roulette gambling law to determine the global optimal solution，which enhances population diversity.With the network loss and voltage offset as the targets，the IEEE30 node system is used to test and calculate the calculation examples，and the results verify the efficiency of the improved AG-MOPSO algorithm in the optimization process.

multi-objective；reactive power optimization；particle swarm；adaptivemesh；Pareto optimal

2016-09-12。

徐基光（1963—），男，硕士，高工，研究方向为电力系统无功电压控制及电压稳定。

（编辑 董小兵）

国家基金资助项目（51405244）。

Project Supported by National Nature Science Foundation of China（51405244）.

1674-3814（2017）02-0021-05

TM72

A