四边形中动点问题的几种情况

安徽省太湖县寺前初级中学(246400)

吉 兴●

四边形中动点问题的几种情况

安徽省太湖县寺前初级中学(246400)

吉 兴●

本文针对四边形中动点问题的不同情况，给出相应的求解方法，对学生学习具有指导意义.

动点；最值；形状；函数

一、动点移动产生的最值问题

最值问题一直与动点有着千丝万缕的关系，在四边形中动点的引入为最值问题提供了良好的背景，此类题多以特殊的四边形为主，我们要掌握四边形的相关知识才能解答.学生在解决此类问题时要注意找出动点的特殊位置进行求解.

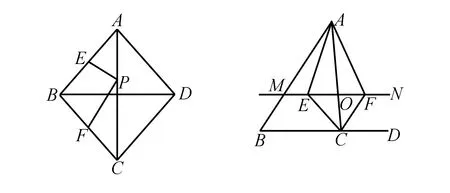
例1 如图所示，四边形ABCD是菱形，BD=6，AC=8.对角线AC上存在一动点P，AB、BC的中点分别为E、F，求PE+PF的最小值.

解析 这是典型的两点在直线同侧求线段和最小值的问题，学生应该对于此类问题的求解方法较为熟悉，就是将同侧的点变为异侧，然后根据三角形两边之和大于第三边的性质判断出只有三点在同一直线时和最小.故作F关于AC的对称点F′，此点也为CD的中点，连接EF′，交AC于点P，此时EF′就是线段和的最小值.由于四边形ABCD为菱形，所以存在EB平行且等于CF′.故四边形EBCF′为平行四边形，EF′=BC.由菱形对角线互相垂直可求出BC=5.故PE+PF最小值为5.

本题中不光是对于求最值问题方法的考察，对菱形性质的检验也体现的很到位.我们要对题目有充分的认识，看到题中所提到的图形，我们就应该在脑海中浮现出该图形的各种性质，这就需要学生对于知识反复记忆并使用.

二、由动点产生的动态图形形状判定

点的移动必然会带来图形形状的变化，在初中数学平面几何部分学到的特殊四边形有可能在变化出现，出题者正是抓住了这点，经过反复推敲就出现了此类问题.学生要熟记特殊四边形的证明方法才能正确解答.

例2 点O为如图所示的△ABC中AC边上的一个动点，过点O作直线MN∥BC，设点E、F分别为MN与∠ACB的平分线及∠ACB的外角平分线的交点.

(1)四边形AECF为矩形时O点的位置，说明理由；

(2)四边形AECF是正方形时点O的位置以及△ABC满足的条件，说明理由.

解析 分析两问，对于正方形的证明是建立在四边形为矩形的基础上的，我们只要证明出何时为矩形，就能使问题得以解决.由题中提到的角平分线可知∠ECF=90°，故我们只需证明何时为平行四边形就可以了.动点的好处在于点O可以出现在AC上的任意位置，平行四边形的性质就是对角线互相平分.所以在证明出O为EF的中点后问题就得证了.由直线MN∥BC及角平分线可知，∠OEC=∠OCE，∠FCO=∠CFO，因此有EO=CO=OF.当O为AC中点时四边形AECF为矩形.而在(2)问中，只需要讨论△ABC应满足的条件就可以.在满足矩形的条件下要证明图形为正方形，一种方法是证明邻边相等，一种是对角线互相垂直.显然在此题中证明角是很简单的，即当∠ACB为直角时满足对角线垂直.

此题中对于动点的讨论更为深入，将几何证明问题与动点的结合更加考验学生的逻辑思维能力.在解决此类问题时我们可以运用逆向思维，先根据要证明的图形的性质确定动点位置，再进行后续过程的证明.

三、与动点有关的函数关系

前面两种情况介绍的都是更加注重于几何图形的证明，而此类问题将函数与平面几何相结合着重考查的是学生的计算能力.这就需要学生将函数知识与几何图形联系在一起，在增加出题多样性的同时也检验了学生的综合能力.

例3 如图所示，有一四边形OABC是矩形，线段BC上存在一动点D(不与端点B、C重合)，直线y=-x+b过点D与折线OAB相交于点E.点A、C的坐标分别为(3,0)，(0,1).记△ODE的面积为S，求S与b的函数关系式.

解析 题中已经很明确地给出点E在折线OAB上，相当于提醒我们情况有两种，一种是E在OA上，另一种是E在AB上.针对第一种情况我们只需求出OE的长以及高即可，是较为简单的.第二种情况，我们就不能再通过底乘以高来求了，因为求这两个的过程繁琐，计算量也很大.这时我们就可以利用矩形面积减掉几个直角三角形的面积来求.先通过极限情况确定在不同直线上b的取值范围，再按照上述思路求解.当直线过A点时，求出b=3/2.当直线过B点时，b=5/2.直线过C点时，b=1.如下面两图所示(1)当E在OA上时，即1

本题中以分类讨论的思想为前提，结合三角形面积的计算以及范围的选取进行完整的解答.数形结合思想的运用让我们更好地对第二种情况进行求解.多种数学方法以及技巧的应用组成了解此题的要点，值得我们深入分析讨论.

纵观全文，三种不同情况的介绍也展示了四边形中动点问题的多样出题思路.学生在解决此类问题时必须要熟练掌握几何证明、函数求解、图形性质等多方面知识，运用逻辑思维能力将它们联系在一起综合运用，求出正确答案.

G632

B

1008-0333(2017)08-0037-01