夯实基础找方法 一题多解拓思路

广东省广州市番禺区化龙中学(511400)

李立平●

夯实基础找方法 一题多解拓思路

广东省广州市番禺区化龙中学(511400)

李立平●

数学的世界丰富多彩，一道数学题可以用一种方法去解答，还可以用多种方法去解答，这就是我们经常运用到的一题多解.

数学;一题多解;中考

一、试题呈现

(2015年广州中考第23题)如图9，AC是⊙O的直径，点B在⊙O上，∠ACB=30°.

(1)利用尺规作∠ABC的平分线BD，交AC于点E，交⊙O于点D，连接CD(保留作图痕迹，不写作法)；

(2)在(1)所作的图形中，求△ABE与△CDE的面积之比.

解法1 作OF⊥BC，设⊙O的半径为r,∴DF=CF

解后分析 有关弦的问题，常作其弦心距(有时还须作出相应的半径)，通过垂径定理，来沟通题设与结论间的联系.

解后分析 在题目中若已知圆的直径，一般是作直径所对的圆周角，利用“直径所对的圆周角是直角”这一特征来证明或求解.

解法3 连接OD,设⊙O的半径为r.

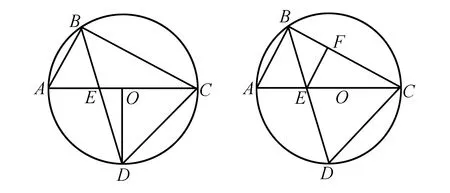
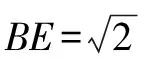
解后分析 由于题中的已知条件中有直角三角形，通过做辅助线构造直角三角形，得到两个三角形相似，利用相似三角形的面积比是相似比的平方得到答案.

二、解题反思

1.抓解题关键，建构方法体系

以上四种解法殊途同归，又各具特色，其关键是抓住基本图形和等量关系，添加适当的辅助线将看似复杂的的图形转化为基本图形.在解决问题时，要注意从数量和图形两方面寻求突破，多积累解题经验，建构解决问题的方法体系.

2.辨解法优劣 ，优化解题方法

本题方法虽多，但是各有优劣，如解法4作EF⊥BC构造直角三角形，这种方法在圆中的辅助线一般比较少，见弦作弦心距和见直径作圆周角这两种方法学生平时接触得比较多，容易理解.在平时组织学生做题时，要引导学生及时总结解题方法并仔细辨析方法的优劣，掌握题型的最优解法.

3.寻方法本质，渗透数学思想

在多种解法中，我们不难发现，其本质就是用了转化和方程思想.从最基本图形入手，抓住相似三角形，直角三角形等基本图式，寻找与本题的关联点进行转化，还有方程思想，在不知道半径的具体长度时可以直接假设⊙O的半径为r，设而不求，用半径r表示线段的长度.

一题多解不仅可以开拓学生的思维能力，找出最佳的解题方法，从而提高解题效率，又可激发学生的学习兴趣.要想掌握一题多解的方法，平时就要重视夯实基础.只有把基础打好了，在解题过程中多动脑筋，多找方法，才能顺利解答各种难题.

[1] 史宁中.感悟数学思想 积累数学活动经验[M].数学课程标准(2011)解读.

[2] 徐秀峰. 数形巧突破 转化妙解题[J].中学数学教学参考(初中版),2015(5).

G632

B

1008-0333(2017)08-0031-01