组合雾化过程中熔滴的飞行动力学与热历史的数值模拟
耿江江,刘允中,王腾
(华南理工大学 国家金属材料近净成形工程技术中心,广州 510640)
组合雾化过程中熔滴的飞行动力学与热历史的数值模拟
耿江江,刘允中,王腾
(华南理工大学 国家金属材料近净成形工程技术中心,广州 510640)
采用数值模拟方法研究组合雾化过程中熔滴的飞行动力学以及冷却凝固过程与熔滴随飞行距离的变化关系,模拟过热度和旋转盘转速对熔滴飞行和冷却凝固的影响规律。结果表明:在组合雾化过程中,熔滴尺寸显著影响熔滴的动力学和热历史过程,熔滴越小,速度变化越快,飞行距离越短。过热度对于熔滴的冷却凝固影响不明显,但大的过热度会延缓熔滴的凝固过程。因此,大的过热度不利于雾化室的设计。旋转盘的旋转速度对于熔滴热历史的影响稍大于过热度的影响,高转速可以缩短熔滴冷却凝固过程的飞行距离。通过测量二次枝晶间距,推算出实验制得粉末的冷却速率范围为103~106K/s,与数值计算的结果基本一致。
组合雾化;动力学;热历史;熔滴直径;过热度;旋转盘速度;二次枝晶间距
组合雾化法是一种新的制粉工艺,它是由多级雾化法[1-2]衍生过来的。采用组合雾化法制备的金属粉末球形度好、纯度高、含氧量低、粒度细、粒度分布窄、卫星颗粒很少,具有好的流动性和均匀的铺展性,且成本低,可大量生产,近年来受到很多人的关注。组合雾化法把自由气雾化和离心雾化有效地结合起来,其工作原理为:将金属熔体过热到一个较高的温度,进行低压自由气雾化,将金属熔体雾化成较粗的熔滴,并同时使之进入高速旋转装置,在高速旋转盘上形成薄而稳定的液膜,当液膜到达旋转盘边缘时,被离心雾化成更细的熔滴,在随后的飞行过程中凝固成固态粉末。熔滴凝固前和凝固时温度随时间的变化对于熔滴最终的组织和粉末形貌有极显著的影响,并且,熔滴到达高速旋转盘之前的飞行轨迹对于雾化室尺寸的设计具有重要的指导作用。因此,了解和掌握组合雾化的关键工艺参数(如过热度和旋转盘转速等)对熔滴热历史(即熔滴凝固前和凝固时的温度随时间的变化)和飞行轨迹的影响规律十分重要。目前,有人对单级离心雾化[3]和喷射成形过程[4-6]的熔滴动力学和热历史进行了数值模拟,LIU等[7]模拟了多级雾化过程中熔滴的热历史,但尚未有对组合雾化数值模拟的报道。实际的组合雾化是一个更复杂的过程,难以用实验方法获得雾化和飞行过程中熔滴动能和热历史的数据。本文作者对组合雾化过程中熔滴的飞行轨迹和凝固情况进行数值模拟,为之后的实验研究提供一定的理论基础。
1 理论模型
1.1 熔滴的飞行动力学
本文基于以N2为雾化介质,采用组合雾化法制备AlSi10Mg合金粉末进行研究。根据组合雾化的特点,将合金熔滴的飞行过程和热历史分为气雾化和离心雾化2个阶段。由于在雾化时,液态金属被粉碎,形成由不同直径的熔滴构成的喷射体,一般来说,喷射体内的熔滴尺寸遵从对数正态分布[8],所以可用质量中位径dm表征喷射体内熔滴的尺寸特征,并可用dm尺寸的单个熔滴代表整个喷射体来研究熔滴的飞行过程和热历史。
1.1.1 气体雾化阶段
经气体雾化而形成的合金熔滴在高速气流的作用下作加速运动进入高速旋转装置,其运动规律直接影响熔滴与气体之间的热交换。熔滴在气流场中作加速运动,可用牛顿运动方程表示[9]:
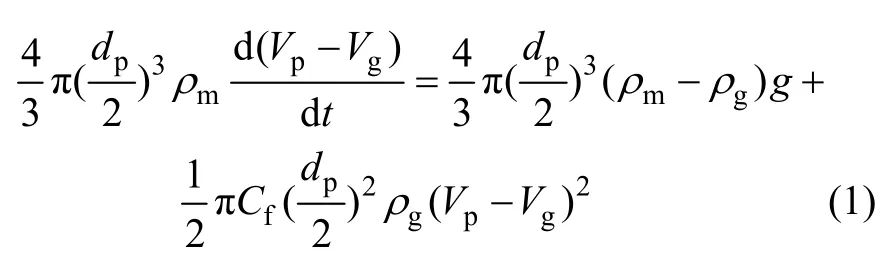
式中:dp为熔滴的平均直径;Vp和Vg分别为熔滴和雾化气体的速度;g为重力加速度,g=9.8 m/s2;Cf为阻力系数,为雷诺数,Re=其中,Vr为相对速度,μg为气体粘度;ρg是 N2的密度;ρm是熔滴的密度;t是熔滴的飞行时间。
雾化气体速度的轴向衰减规律[6]为:
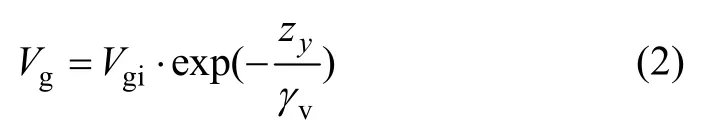
式中:Vg为轴向气体速率;Vgi为雾化器出口处的初始轴向气体速度;zy为轴向距离;γv为衰减系数,γv=a1Vgin。其中:a1=3.04×10-4m-0.24s1.24,n=1.24。
气体的初速度与气体雾化压力直接关联,根据气体动力学原理[10]:
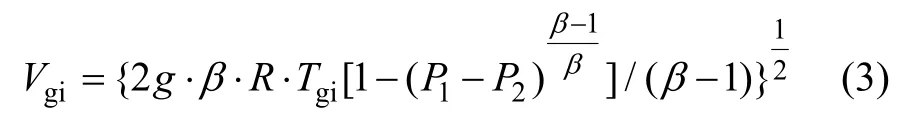
式中:g为重力加速度,9.8 m/s2;R为气体常数,R=8.3 J/(mol·K);β为压容比,(Cp是比定压热容,Cv是比定容热容);Tgi为压缩气体进喷嘴前的温度,一般为室温298 K;P1为大气压力,P2为雾化气体压力。
用式(1)即可求得合金熔滴的运动规律,由于气雾化阶段的熔滴飞行距离较小,计算结果表明熔滴一直仅作加速运动。
1.1.2 离心雾化阶段
旋转盘边缘的熔滴具有与旋转盘边缘相同的切向速度,利用下式计算:

式中:n为旋转盘转速;R为旋转盘半径。旋转盘边缘的熔滴在气体的拖拽力下运动,其运动方程[9]为:
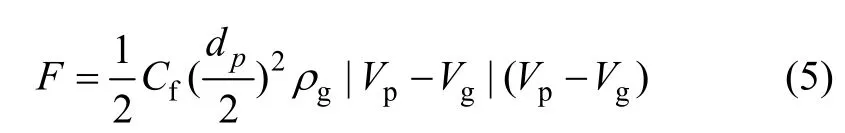
熔滴被离心后,在水平方向上雾化介质的速度随飞行距离的变化为:
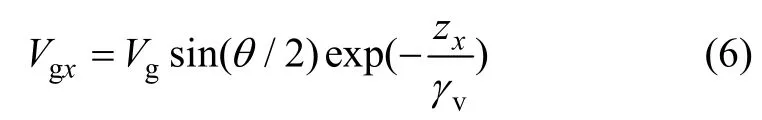
式中:Vgx为雾化介质水平方向速度;Vg为轴向气体速率;θ为雾化角;zx为水平距离。
1.2 熔滴尺寸的变化
在气雾化阶段,根据Lubanska公式[11]:
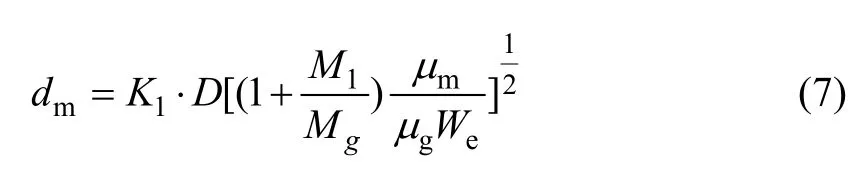
式中:dm为熔滴的平均尺寸;K1为常数,K1=40~50,这里K1取50;D为液流直径;Ml和Mg分别为金属熔体与雾化气体的质量流率;μm和μg分别为金属熔体与气体的运动粘度。
在离心雾化阶段,熔滴平均尺寸dm的计算公式[12]为:
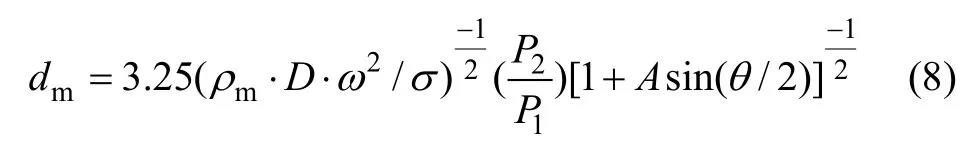
式中:σ为金属熔体的表面张力;ω为离心盘的转速;A为常数,根据现有的雾化设备,A取7.255。
1.3 熔滴的传热规律
在气雾化点(金属液体从漏包底小孔顺着环形喷嘴中心孔轴线自由落下,雾化气体由环形喷口高速喷出形成一定的喷射顶角,而环形气流构成一封闭的倒置圆锥,于顶点交汇,此顶点即气雾化点),金属熔体的温度远远高于雾化介质的温度,因此熔滴的传热主要通过熔滴表面的热对流,热辐射可以忽略。假设熔滴的冷却符合牛顿冷却条件,忽略熔滴内部温度差,则热传递系数h可表示为[13]:
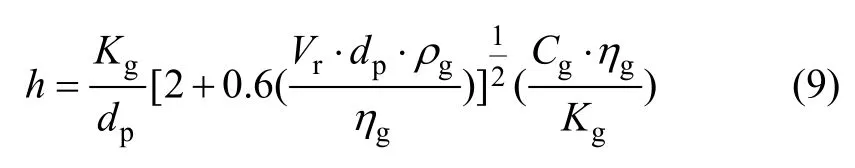
熔滴通过与气体的对流而损失热量,导致熔滴温度降低,这一过程可表示为[6]:
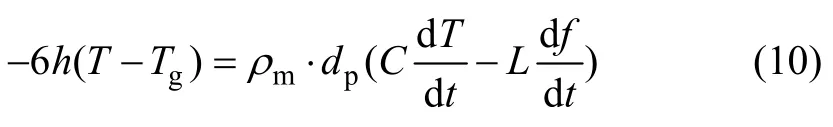
式中:T和Tg分别为熔滴和气体的温度;C与L分别为熔滴的比热容和液体金属的熔化潜热;f为熔滴的凝固分数。飞行过程中,熔滴以对流方式把热量传递给环境,熔滴温度逐渐降低。对AlSi10Mg合金而言,熔滴经历5个阶段:液相冷却、形核与再辉(再辉是由于快速凝固过程结晶潜热的释放速率大于熔滴表面的热交换,熔滴温度迅速升高,使得金属出现重熔的现象。)、偏析凝固、共晶转变和固相冷却。
1.3.1 液相冷却
在液相冷却阶段,熔滴将热量传递给环境,自身温度降低,固相含量一直为零,直到形核温度Tn。在这一阶段,熔滴的热损失由熔滴的焓所补偿。根据传热学基本原理,该冷却过程的温度变化可用下式表示:
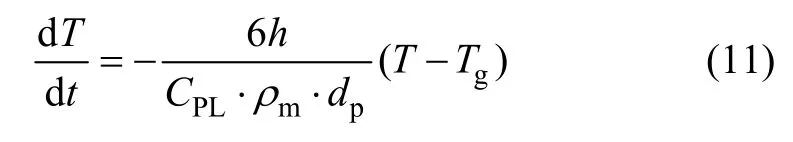
式中:CPL为熔滴的液态比热容;Tg为雾化介质的温度;ρm是熔滴的密度;dp为熔滴的平均直径;T为熔滴的温度,h为热传递系数;t是时间。一般认为气体喷射流在开始(出口处)的温度 Tgi和终了温度 Tgf分别为25 ℃和75 ℃,在这个温度增加区间,气流的温度与喷射距离呈指数规律增长,即[6]:
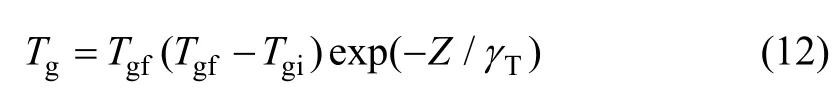
式中:γT为常数,一般取0.1 m。
1.3.2 形核与再辉
熔滴冷却到液相线时,由于缺乏形核质点,并不立刻发生形核,而是过冷到一定的温度,即达到形核温度。由于组合雾化过程中,冷却速率相对较小,假设过冷度为30~60 ℃。在这一阶段,放出的热量远大于熔滴传给环境的热量,熔滴温度升高,产生再辉。在组合雾化中,熔滴的尺寸相对较小,凝固过程符合壳状模型,熔滴的凝固相体积分数可表示为[10]:
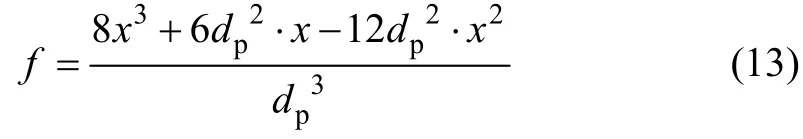
式中:x为固液界面移动的长度;dp为熔滴的平均直径。
晶体生长速度为:

式中:K为熔滴中固液界面的移动速率,K≈0.01 ms/K;ΔT为熔滴的过冷度[14]。
熔滴的温度和凝固相的体积分数变化分别用下式计算:
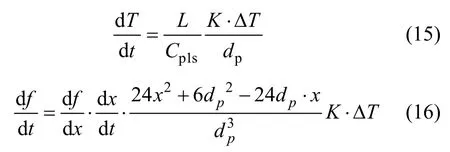
式中:Cp1s表示固、液混合体的比热容。

1.3.3 偏析凝固
再辉过程中,随熔滴温度升高,熔滴的潜热释放率降低,当熔滴内部潜热释放率等于表面散热速率时,再辉结束,熔滴开始偏析凝固。再辉温度Tr表示为[6]
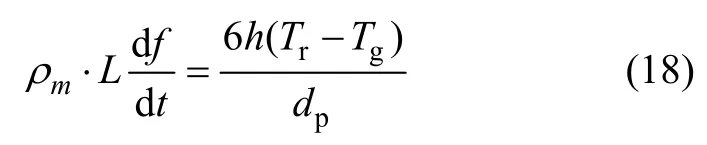
偏析凝固过程可用Scheil方程[15]近似表示为:
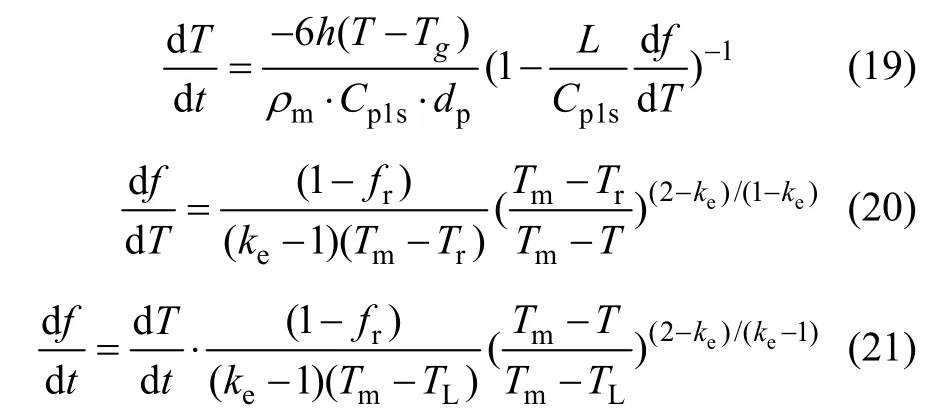
式中:fr为再辉结束时凝固相的体积分数;Tm为基体金属的熔点;TL为AlSi10Mg合金的熔点;ke为溶质平衡分配系数;h是热传递系数;L为熔化潜热。
1.3.4 共晶转变
当偏析凝固过程进行到共晶转变温度时,熔滴中剩余液相发生共晶转变。在共晶转变期间,熔滴温度一直保持在共晶温度,直至凝固结束。该过程中凝固分数可表示[16-17]为:
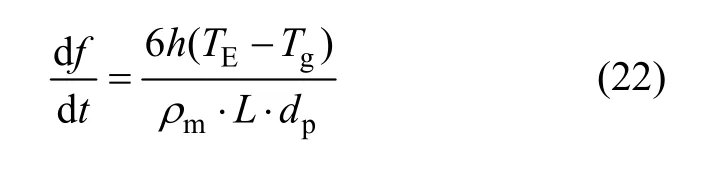
1.3.5 固相冷却
固相冷却阶段,熔滴通过对流传热使温度降低,温度变化符合下式[18]:
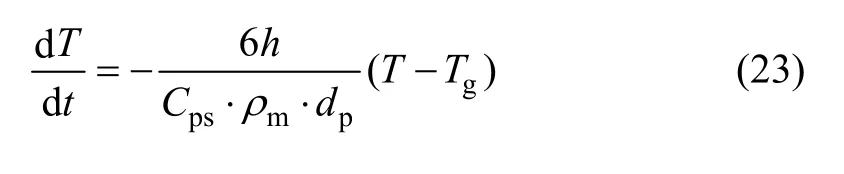
2 雾化过程计算
式(1)~(23)是一阶非线性常微分方程,采用经典四阶RungeKutta方法即可求得在一定工艺条件下,雾化过程中熔滴的速度、温度、凝固相体积分数、冷却速率等参数随飞行距离的变化。假设熔滴在dt时间内连续加速,相应的距离dZ与dt间的关系可用下式表示:

式中:u为时间dt内的初始速度;v为时间dt内的结束速度。dZ的取值足够小,以保证计算的精确性。为了简化计算,做如下假设:
1) 所有熔滴都是球形,在气雾化点,熔滴的轴向距离为零,熔滴速度为零。
2) 所有熔滴之间没有相互影响。
3) 所有熔滴的物性参数的动态变化只受雾化气流的影响,忽略气体紊流对熔滴的影响。
4) 在离心雾化前,对离心盘进行预热,并且由于组合雾化工艺中离心盘的转速很高,形成的液膜在离心盘上停留的时间很短,所以忽略熔滴在离心过程中温度的变化。
雾化合金 AlSi10Mg和雾化介质氮气的热物性参数列于表1。
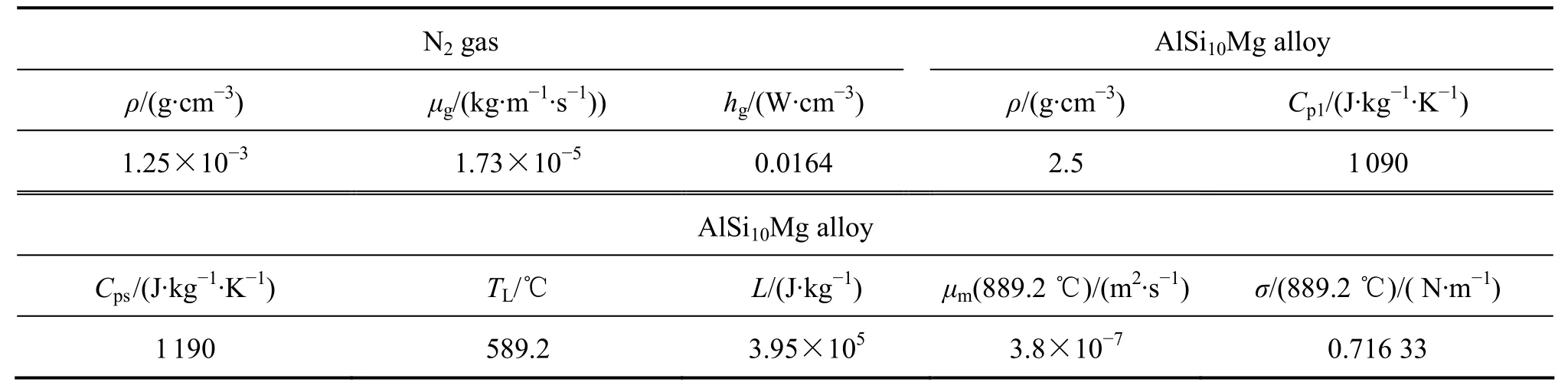
表1 雾化合金AlSi10Mg和雾化介质氮气的热物性参数Table 1 Physical properties of AlSi10Mg alloy and N2gas
3 计算结果与讨论
3.1 数值计算结果
图1所示为熔滴速度、凝固相体积分数、熔滴温度、传热系数、冷却速率以及气体与熔滴的相对速度随飞行距离的变化。气体初速度为260.735 m/s,雾化点到离心盘的距离为7.67 cm,金属液流直径D为4.2 mm。
图 1(a)所示为组合雾化过程中熔滴的速度变化。在气雾化阶段,在气体拖拽力和自身重力的作用下,熔滴一直加速,直至撞到离心盘上。熔滴撞到离心盘时,轴向速度迅速衰减为 0。在离心力的作用下,熔滴由于粘性力在离心盘上形成一层流动的液膜。在离心盘的边缘处,由于惯性与表面张力的作用,液膜分裂成熔滴,熔滴的切向速度远大于径向速度,因此认为离心盘边缘处熔滴的水平速度约等于熔滴的切向速度,即离心盘边缘的切向速度。因为液膜在盘边缘处分裂形成的熔滴的水平方向速度小于之前的轴向速度,所以存在较大的速度差。经过离心雾化后形成更细小的熔滴,随后在环境中做减速运动。在整个过程中,小直径熔滴速度变化更快,且在气雾化结束时小直径熔滴的最大速度大于大直径熔滴的最大速度。
熔滴的凝固主要发生在离心雾化之后。从图1(b)可知,在液相冷却阶段,固相的体积分数为零。再辉过程中,由于过冷液相中形核和冷却速率非常快,所以固相的体积分数急剧增加,再辉结束时,固相体积分数在0.1左右。偏析凝固期间,凝固速度降低,熔滴固相分数增加率较小。共晶转变期间,凝固速度增加,共晶转变结束时,固相体积分数为 1。固相体积分数的模拟计算可为雾化室的设计提供一定的理论基础。
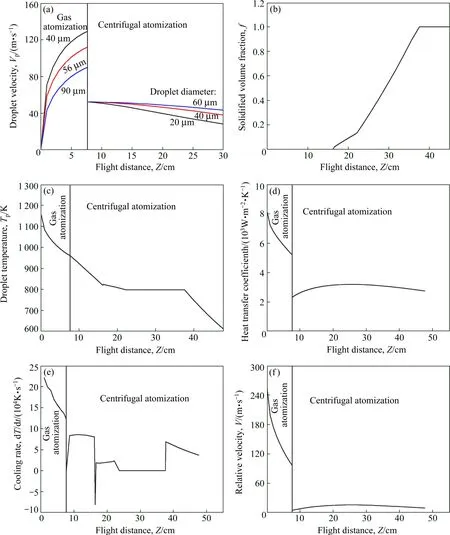
图1 熔滴的动力学与热历史Fig.1 Dynamic and thermal history during flight of droplets
图 1(c)所示为熔滴温度的变化。熔滴温度的变化主要与熔滴的对流传热强度有关。从图 1(c)可见,在气雾化阶段,主要发生熔滴的液相冷却。离心雾化之后,熔滴粒径减小,但因熔滴与周围气体之间的相对速度减小,对流传热强度变差,所以熔滴的温度变化幅度与气雾化阶段相差不大。当达到一定的过冷度时,熔滴开始形核和再辉,在形核和再辉阶段熔滴内部潜热释放率大于表面散热速率,温度快速上升,但达到的最高温度仍然低于熔滴的熔点。因此,过冷度也大大减小。凝固主要由再辉与内部潜热的释放决定。形核与再辉时间很短,因此熔滴的飞行距离很小。偏析凝固期间,熔滴温度的变化速率不大,直到共晶温度。共晶期间,温度不变,直至熔滴变为全固相。然后,熔滴进入固相冷却阶段。
传热系数主要与熔滴直径、熔滴及气流的相对速度有关。如图1(d)所示,在气雾化点,气体速度最大,熔滴速度为零,相对速度最大,因此传热系数最大。随后,在气雾化阶段,气体速度呈指数衰减,熔滴速度增加,导致熔滴与气流的相对速度减小,传热系数随之减小。当熔滴到达离心盘时,熔滴速度发生急剧变化,所以传热系数产生突变。在旋转盘边缘形成的熔滴在离开旋转盘后,在气体的拖拽力下减速。离心雾化之后,熔滴粒径减小,但熔滴与气流的相对速度较小,传热系数没有气雾化阶段大。离心雾化之后,传热系数先缓慢增加,到达一定值又缓慢减小。
熔滴飞行过程的冷却速度是温度对时间的微分。由于熔滴温度降低的阶段性特征,因而熔滴飞行过程中冷却速度的变化也较复杂。冷却速率的变化主要和传热系数、熔滴与气体之间的温差有关。图 1(e)所示为熔滴的冷却速率随飞行距离Z的变化。在Z=0时,传热系数和熔滴与气体之间的温差均最大,因而冷却速率最大。随飞行距离增加,传热系数以及熔滴与气体之间的温差逐渐减小,冷却速率逐渐减小。离心雾化后,熔滴与气体之间的温差仍在减小,但传热系数增大,冷却速率增大,到达一定值后减小。当熔滴开始形核再辉时,由于潜热的释放,熔滴温度迅速上升,冷却速率出现负值。再辉结束开始偏析凝固时,熔滴又以极大的速率冷却。熔滴温度达到共晶温度时,熔滴开始共晶反应,温度保持不变,冷却速率为 0。熔滴完全凝固后,开始固相冷却,因传热系数降低,冷却速率降低。通过计算不同粒径熔滴的冷却速率,可得出熔滴冷却速率的范围为103~106K/s。
熔滴与气流的相对速度的变化主要和熔滴的运动状态有关。在气雾化出口处,气体速度最大,熔滴速度为 0,气雾化过程中,熔滴在自身重力和气体拖拽力的作用下作加速运动。因喷射距离短,在到达离心盘之前,熔滴一直保持加速状态,气体速度呈指数衰减,因此熔滴与气流的相对速度减小(如图1(f)所示)。由图 1(c)的熔滴速度变化,可以得出离心雾化之后熔滴与气流的相对速度的变化趋势。
图2所示为熔滴的过热度对熔滴温度和凝固进程的影响。由图可见,熔滴过热温度对于其冷却和凝固过程影响不大。当熔滴的过热度增加时,其表面张力减小,形成更细的熔滴,因此冷却速率增加,整个凝固过程所用时间减少。但细化的熔滴与增加的过热度相比,并没有使得熔滴提前凝固。熔滴温度越高,熔滴冷却到形核温度所需的时间更长。从图2(a)可看出,过热度对于熔滴凝固结束时的飞行距离有一定的影响:过热度越大,熔滴的飞行距离越大,为了保证熔滴在碰到腔室壁前完全凝固,这就要求更大的雾化室。
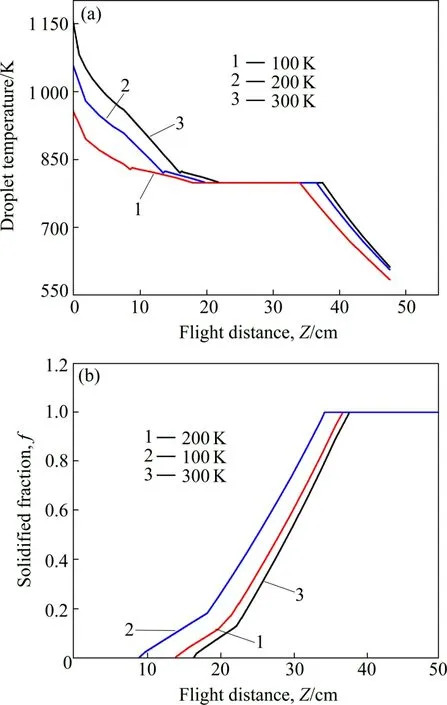
图2 过热度对熔滴温度和凝固进程的影响Fig.2 Effect of superheat on cooling procedure (a) and solidification procedure (b) of the droplets
图3所示为旋转盘速度对熔滴温度和凝固进程的影响。从图3可见,旋转速度对于熔滴的冷却和凝固过程的影响比过热度的影响更显著。随旋转速度增加,金属液受到的离心力越大,因而熔滴越细。旋转速度越大,在盘边缘形成的熔滴的切向速度越大,因而熔滴与气体的相对速度越大,使得传热系数增加。而熔滴越小,熔滴自身的焓越少,使得冷却速率增大,熔滴的冷却和凝固过程相应提前,凝固时间缩短,因而完全凝固时的飞行距离也随之减小。所以旋转盘转速较大时在保证熔滴在碰到雾化室器壁时不发生粘壁和进一步破碎的前提要求下,雾化室可设计得小些。
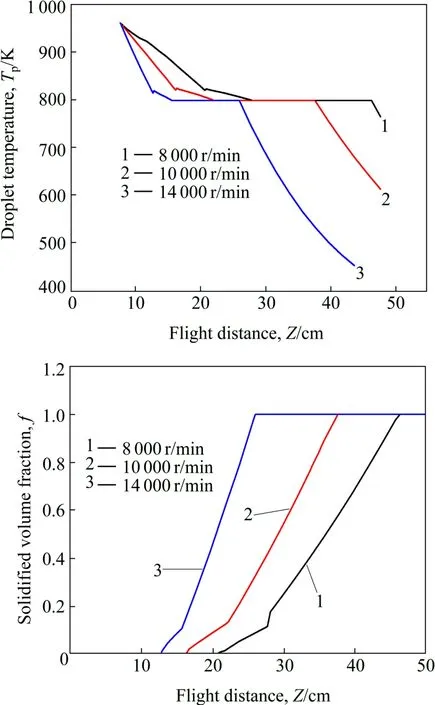
图3 旋转盘转速对熔滴温度和凝固进程的影响Fig.3 Effect of disk rotation speed on cooling procedure (a) and solidification procedure (b) of the droplets
图4所示为熔滴直径对凝固过程的影响。分别以20,40,和60 μm尺寸的熔滴为例,这3种熔滴的凝固过程都发生在离心雾化之后。随熔滴直径增大,凝固开始时间明显推迟。直径为 20 μm的熔滴在18.77 cm时已结束凝固,而直径为60 μm的熔滴在22.67 cm处才开始凝固。尺寸越大,整个凝固过程的持续时间越长。
3.2 实验验证
利用自行设计的雾化装置,采用组合雾化法制备AlSi10Mg合金粉末。具体过程如下:采用中频感应加热装置对AlSi10Mg母体合金加热至预定温度,打开熔炼坩埚中的止通装置,熔融金属在重力和喷嘴出口处抽吸压力作用下通过雾化喷嘴进入雾化室,同时雾化气体氮气对金属液流不断冲击,形成大量弥散的金属熔滴,金属熔滴飞至离心盘,在离心盘上形成一层很薄的液膜,液膜在离心力的作用下粉碎成更细的金属熔滴,最终金属熔滴在雾化室中通过热交换逐渐降温凝固成金属粉末。气雾化压力 P=0.6 MPa,旋转盘的转速n= 8 000 r/min,喷射高度H=17 cm,过热度为300 K。图5所示为铝硅合金雾化粉末的截面组织,由图可见粉末内部有大量的枝晶组织存在。通过金相显微镜观察,测出不同粒径颗粒的二次枝晶间距,然后通过二次枝晶间距估算出合金的冷却速率[19]。对于10~90 μm的颗粒,其二次枝晶间距为0.3~5.0 μm范围,推算出冷却速率范围为103~106K/s,与图1(e)中的数值计算结果基本吻合。
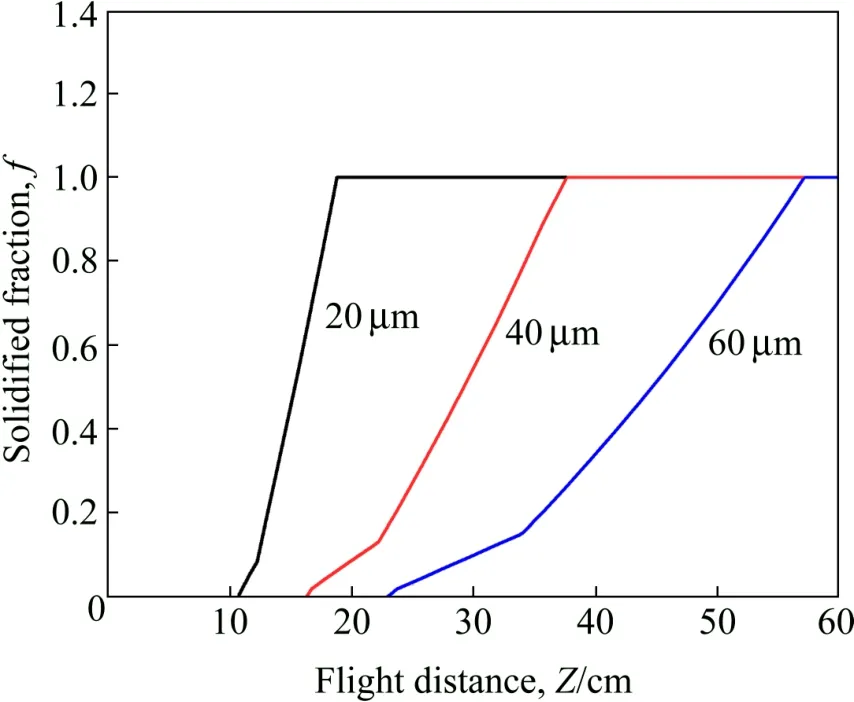
图4 熔滴直径对凝固过程的影响Fig.4 Effect of droplet diameter on solidification procedure
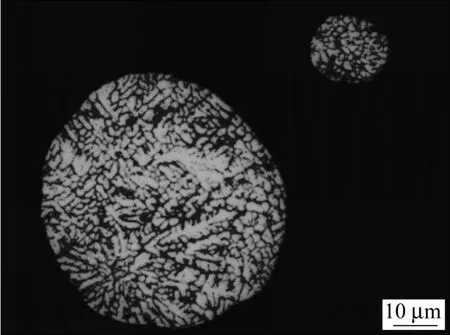
图5 组合雾化法制备铝硅合金粉末的显微组织Fig.5 Microstructure of aluminum silicon alloy prepared by combination atomization
4 结论
1) 在组合雾化法制备金属粉末时,熔滴直径对于熔滴的速度有很大影响。熔滴直径越小,速度变化越快,最高速度也越大。
2) 熔滴的冷却速率主要与熔滴的传热系数和熔滴直径有关。传热系数越大,直径越小,则熔滴的冷却速率越大。
3) 过热度对熔滴的冷却过程影响不明显,过热度越大,熔滴完全凝固时的飞行距离更远,要求更大的雾化室,对于雾化室的设计不利;旋转速度对于熔滴冷却过程的影响比过热度显著,旋转速度越高,熔滴凝固开始和结束的时间均提前,相应地,雾化室可以设计得小一些;熔滴尺寸对熔滴的凝固过程有显著影响,熔滴尺寸减小可以增大过冷度和冷却速率,使熔滴在更短的飞行距离内完成凝固。
4) 通过测量二次枝晶间距,推测实验制得粉末的冷却速率为103~106K/s,与数值计算结果基本吻合。
REFERENCES
[1]LIU Yunzhong, MINAGAWA K, KAKISAWA H, et al. Melt film formation and disintegration during novel atomization process[J]. Transactions of Nonferrous Matals Society of China, 2007, 17(6): 1276-1281.
[2]LIU Yunzhong, KAKISAWA Ha, HALADA K. Production of fine metallic powders by hybrid atomization process[J]. The Japan Society of Mechanical Engineers, 2003, 46(3): 260-264.
[3]李会平, TSAKIROPOULOS P. 旋转盘离心雾化熔滴飞行动力学与凝固进程[J]. 中国有色金属学报, 2006, 16(5): 793-799. LI Huiping, TSAKIROPOULOS P. Droplet dynamic and solidification progress during rotating disk centrifugal atomization[J]. The Chinese Journal of Nonferrous Metals, 2006, 16(5): 793-799.
[4]袁武华, 陈振华, 徐海洋, 等. 多层喷射沉积耐热铝合金管坯热流分析(I)-雾化过程热流分析[J]. 湖南大学学报, 2004, 31(1): 7-11. YUAN Wuhua, CHEN Zhenhua,XU Haiyang, et al. Heat flow of multi-layers spray deposited heat-resistant Al alloy pipe blank[J]. Journal of Hunan University, 2004, 31(1): 7-11.
[5]张永安, 熊柏青, 刘江, 等. 喷射成型过程中雾化粒滴的数值模拟[J]. 中国有色金属学报, 1999, 9(1): 78-82. ZHANG Yongan, XIONG Baiqing, LIU Jiang, et al. Numerical simulation of the droplets during spray forming[J]. The Chinese Journal of Nonferrous Metals, 1999, 9(1): 78-82.
[6]GRANT P S, CANTOR B, KATGERMAN L. Modelling of droplet dynamic and thermal histories during spray forming:ⅠIndividual droplet behavior[J]. Acta Metallurgica, 1993, 41(11): 3097-3108.
[7]LIU Yunzhong, CHEN Zhenhua, WANG J N. Numerical simulation of the thermal history droplets during multi-stage atomization[J]. Science& Technology of Advanced Materials, 2001, 2(1): 177-180.
[8]PRYDS N H, HATTEL J H, PEDERSEN T B, et al. An integrated numerical model of the spray forming process[J]. Acta Materialia, 2002, 50(16): 4075-4091.
[9]沈军, 蒋祖龄, 曾松岩, 等. 雾化沉积快速凝固过程的计算机模拟-Ⅰ. 理论模型[J]. 金属学报, 1994, 30(8): 337-341. SHEN Jun, JIANG Zuling, ZENG Songyan, et al. The numerical simulation of rapid solidification during spray deposition process-Ⅰ. Theoretical model[J]. Acta Metallurgica Sinica, 1994, 30(8): 337-341.
[10]梁红玉. 微纳米晶高Si铝合金材料制备工艺及组织形成机理研究[D]. 上海: 上海大学, 2006: 57-64. LIANG Hongyu. The research of manufacturing process and microstructure evolution of micro-nanostructured high-silicon aluminum alloys[D]. Shanghai: Shanghai University, 2006: 57-64.
[11]LUBANSKA H. Correlation of spray ring data for gas atomization ofliquid metals[J]. Journal of Metals, 1969, 22(2): 45-53.
[12]LIU Yunzhong, MINAGAWA K, KAKISAWA H, et al. Hybrid atomization: Processing parameters and disintegration modles[J]. The International Journal of Powder Metallurgy, 2003, 39(2): 29-37.
[13]傅晓伟, 张济山, 孙祖庆. 喷射沉积过程的计算模型及优化软件[J]. 金属学报, 1999, 35(2): 147-151. FU Xiaowei, ZHANG Jishan, SUN Zuqing. Modeling and optimizing software of spray deposition process[J]. Acta Metallurgica Sinica, 1999, 35(2): 147-151.
[14]LEVIC G, MEHRABIAN R. Heat flow during rapid solidification of under cooled metal droplet[J]. Metallurgical Transaction, 1982, 13(2): 221-234.
[15]LEE E S, AHN S. Solidification progress and heat transfer analysis of gas-atomization alloy droplets during spray forming[J]. Acta Metallurgica ET Materialia, 1994, 42(9): 3231-3243.
[16]LAWRYNOWICZD E, LIB, LAVERNIAE J. Particle penetration during spray forming and co-injection of Ni3Al+ B/Al2O3intennetallic matrix composite[J]. Metallurgical & Materials Transaction B, 1997, 28(5): 877-897.
[17]SEOK H K, OH K H, RA H Y, et al. A three-dimensional model of the spray forming method[J]. Metallurgical & Materials Transactions B, 1998, 29(3): 699-708.
[18]MATHUR P, APELIAN D, LAWLEY A. Analysis of the spray deposition process[J]. Acta Metallurgica, 1989, 37(2): 429-443.
[19]MATYJA H, GIESSEN B C, GRANT N J. The effect of cooling rate on the dendrite spacing in splat-cooled aluminum alloys[J]. Journal of the Institute of Metals, 1968, 96(1): 30-32.
(编辑 汤金芝)
Numerical simulation of droplet flying dynamic and thermal history in the process of combination atomization
GENG Jiangjiang, LIU Yunzhong, WANG Teng
(National Engineering Research Center of Near-net-shape Forming Technology for Metallic Materials, South China University of Technology, Guangzhou 510640, China)
A mathematical model was established to describe the in-flight dynamics and thermal history of droplets as a function of flying distance during combination atomization. It was developed to simulate the influence of superheat and rotational speed on the flight and solidification of droplets. The results show that the droplet diameter has an obvious effect on dynamic and thermal behavior of combination atomized droplets. With decreasing droplet diameter, the velocity of droplets changes quickly and the flight distance becomes short during solidification of the droplets. The droplet superheat has a weak effect on cooling rate and solidification. However, large superheat would delay the solidification process of the doplets, which is not conducive to the design of the atomization chamber. Rotational speed has a slightly greater influence on the droplet thermal history than the superheat. A higher rotational speed can shorten the flight distance during solidification. This paper calculates the cooling rate of the powder by measuring the secondary dendrite spacing, which ranges from 103to 106K/s and is consistent with the numerical calculation results.
combination atomization; dynamics; thermal history; droplet diameter; superheat; rotational speed; the secondary dendrite spacing
TF123.112
A
1673-0224(2017)01-1-08
广东省科技计划资助项目(2014B010129002)
2016-07-27;
2016-10-09
刘允中,教授,博士。电话:020-87110081;E-mail: yzhliu@scut.edu.cn

