基于问题的互助学习
——以 “比例的意义”的教学为例
◇李培芳
学习是个性化的过程,学生的学习速度和学习水平不可能一致,有学习就有差异。然而在班级授课制下,教师往往无法全面顾及活生生的每一个鲜活的个体。于是,学习速度快的学生不得不在一定的程度上“陪学”,陪着学习速度慢的学生慢慢地学;学习速度慢的学生有时候也在“陪学”,他们陪着学习速度快的学生学自己一时无法理解的内容,这是一个问题的两个方面。
学习差异真实存在且无法回避。教学唯一的途径是利用学习形成的差异,不可能也不应当企图消弭学习的差异。然而如何利用学习差异帮助学生学习一直是班级授课制下的难题。据此,我们开展了“基于问题的互助课堂”的研究。我们发现:互助课堂或是一个可行的途径。
一方面,学生是喜欢互助的。在助人方面他们是天生的“慈善家”,对几乎所有人,孩子都有天然给予帮助的自觉自愿,这种自觉的行为本身就是目的,没有附加条件的目的。同时,孩子更愿意接受来自同伴的帮助。特别是在学校的学习中,我们观察了很多师生一对一的交流与学生之间一对一的交流,事实是,不管多么融洽和谐的师生交流都无法与学生之间的交流相比。
另一方面,互助让课堂有质量地“慢”下来了,尤为可贵的是,那是全体学生都能接受的“慢”。以前的“慢”可能是学习速度快的学生听老师重复讲解,现在的“慢”是学习能力强的学生在帮助同伴,同时也在检验自己是否可以完成“成功地帮助同伴完成学习”。在这样的“慢”里,没有人在学习之外。
基于上述思考,我们不断探索基于问题的互助课堂的形态与策略,以期在班级授课制的前提下探寻有效的个别化教学的方式。
本文试图通过“比例的意义”这一教学课例,反映出基于问题的互助课堂的课堂形态与教学方式。这一课例是笔者刚上完的一节常态课,也算是我们研究互助课堂最新的样态吧。
教学过程
一、根据课题提出问题
(教师出示课题:比例的意义)
师:同学们,今天我们要学习“比例的意义”,你们有什么问题要问吗?
生:什么是比例?
生:比例有什么用?
生:比例和比有什么关系?
(教师根据学生的回答,即时板书上述三个问题)
[意图与思考:基于问题的互助课堂,首先要有问题,问题的来源最好来自学生。新课之始,让学生根据学习课题提问题是一种常用且有效的方式。有的老师会觉得这个问题好像成了一种“套路”,很多学习内容都可以这样问,学生一般也都从“是什么”“为什么”“怎么样”三个方面提问题。这种雷同的问题使很多老师甚至都不好意思问了。其实不然,“是什么”“为什么”“怎么样”是一种全面而相对缜密的思考方式,即便是大哲学家也常常这样思考问题。我们发现“就着课题提问题”可以适用于许多教学内容,常问常新,无须回避。]
二、尝试自学解决问题
师:就这三个问题,有两种学习方法供大家选择,方法A是老师将这三个问题向同学们讲了,方法B是同学们自己看书学习,你们选择方法A还是方法B?
(学生都选择方法B并独立看书学习)
[意图与思考:好的教学一定是充分发挥学生学习主动性与积极性的教学,基于问题的互助课堂也不例外。本环节,有的老师可能觉得没有必要,因为学生必然选择B。必然选择的问题还要问吗?其实还是要问的,这一问问出的是对学生的尊重,给出的是学生学习方式选择的权利。这样的做法对学生自主学习意识的建立是有帮助的;另一方面,也旨在培养学生对学习的责任意识,因为学习方式是自己选的,学习责任也就需要自己去承担。]
三、同伴互助交流所得
师:这样,每位同学对这三个问题都有自己的想法,请每个小组的B同学将自己的想法与A同学说一说。A同学认真倾听并负责在观点不同的地方提出来讨论。
教师重点观察学习困难较大的学生所在小组的讨论情况。以观察结果为根据,确定下一环节全班讨论时“讨论什么”。
[意图与思考:基于问题的互助课堂,互助是学习的重要方式,同桌两人以A同学、B同学作区分,在互助的具体环节中,相对难的问题由学习能力较强的A同学阐明观点,相对简单的问题由B同学阐述观点。交流时,一般是同桌交流,同桌交流可以保证学生交流时不 “溜号”且交流的频率高。当同桌无法解决问题时,根据情况可以向前后桌寻求帮助,或者保留问题在全班讨论时提出。]
四、师生交流深入学习
师:有没有同桌互助无法解决的问题?
生:“比例有什么用”我们好像不太明白。
师:有同样问题的请举手(约三分之一的同学举手)。这样,咱们先来确认前两个问题是不是清楚了(学生表示都清楚了)。那请大家合上书,老师检查一下大家的学习情况。谁能说说什么是比例?
生:就是两个比,比值相等。
生:就是用等号把两个比连起来,有四个项的式子。
生:1∶3=2∶6,这就是比例。
师:大家能举例,也知道比例是什么样子,但是无法说出什么是比例,说明大家还需要学会归纳总结。什么是比例呢?比例就是表示两个比相等的式子。用什么来表示它们相等呢?用等号。来,同桌之间互相说说什么是比例。
(即时巩固:同桌两个学生分别写一个比例,互助检查)
师:第二个问题,比例和比有什么区别,大家也都清楚了,老师问一个问题,比例和比最大的区别是什么?
生:比例有四个项,比只有两个项,前项和后项。
生:比例有两个比号,比只有一个。
生:比例有等号,比没有。
生:比例有两个比,比只有一个比。
生:比例是等式,比不是等式。
师:同学们觉得哪个回答最好?(大部分认为最后一位同学的回答最好)是啊,前面几位同学发现的是它们表面的不同,这位同学看到了实质上的不同。
师:“比例有什么用”同学们普遍觉得有困难,我们等会儿集中来讨论。
[意图与思考:在基于问题的互助课堂里,教师常常处于不知道教什么的状态,因为你要教的是同学互助无法解决的问题,同学互助能解决的就交给他们自己解决或群体讨论解决。教师可以从如下两方面寻找“互助后该教什么”:一是课堂观察,特别是到“学习困难较大的学生所在小组”那里去观察讨论的情况;二是在深入理解教材与深刻读懂学生的基础上做出教学判断,在这方面教师的经验与学习同等重要。]
五、课堂练习确认学习
1.会举例。
同桌互助:各举一个例子后,判断对方写的对还是错。找出特别好的例子或有错的例子,全班交流。
同桌交流:说出自己举例的方法,让同伴按照你说的方法再举一个例子。
2.会判断。
和 0.15∶0.45能否组成比例。
(第①题后,教师提醒书写格式)
师:在互助时候有没有发现同学中可爱的错误,说出来给大家提个醒,这对大家都是莫大的帮助。
生:刚才某同学求比值时忘变倒数了。
师:谢谢出现错误的几位同学,每一个错误都是一个提醒,错误提醒了你,你可别忘了提醒全班哦。
3.会改错。
师:第②题,如果改动其中一个数,让它能组成比例,你会改吗?
(学生尝试,汇报交流)
4.会创造。
①用10以内的自然数创造一个比例。
②用12的因数创造一个比例。
③用10以内的合数创造一个比例。
说明:题③没有答案,老师抱歉地表示出错题了。其实这是老师故意出错,这个错让学生的思考强度有不小的增强,同时让课堂更好玩了些。
[意图与思考:在基于问题的互助课堂里,学习发生在学生之间的比较多,老师教得少,学生到底学得如何,互助是否有效,这是老师很担心的问题,也是该学习方式是否有意义的关键考量。因而,在我们的课堂里,强调保证至少15分钟的练习环节,这个环节通过一些针对性、全面性的问题来确认学生的学习效果。我们发现,学生很喜欢这个环节,因为不只是老师,学生也非常着急地想知道自己的学习效果。学生对问题是有喜好的,因为问题可以照见他们的成功,也能照出他们的不足。]
六、协同互助深度学习
师:下面,我们一起来思考“比例有什么用”。谁愿意分享一下你的思考?
(没人举手,学生面有难色)
1.照片放大与缩小中的比例。
(课件出示图1)
师:哪一张照片,你觉得别扭、不自然,像是被处理过的?

图1
生:右边那张。
师:为什么?
生:因为那张不成比例。
生:因为右边那张看上去,头显得特别大。
师:大家眼力真好,没错,右边的照片老师处理过了,将头拉长了。一般的小孩儿,头与身体的比是1∶4。我们来看看正常放大后应该是怎样的,如图2。
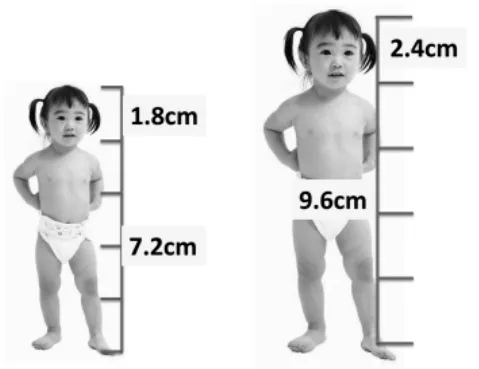
图2
师:从图2中,你能写出几组比例?
(学生写比例,汇报,互查互助。略)
2.影子也是讲比例的。
师:你能找出图3中明显的错误吗?

图3
(学生都能发现影子的长度不对)
师:是这样的,其实影子也是讲比例的。我们接着来看图4。写出你从图中看到的比例。
(学生写比例,汇报,互查互助。略)
3.回到问题:比例有什么用?
师:看了这两个例子,你能说说比例有什么用吗?
生:生活中很多地方存在着比例,学了比例就可以解决生活中的问题。
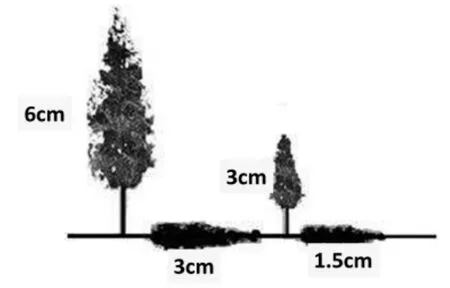
图4
生:可以用比例来判断图片是不是变形了。
生:学了比例,可以运用到生活中。
师:同学们的感觉真好,生活中确实存在着大量的比例,要发现这些比例,就需要有数学的眼光,只有学了比例才能发现比例。当你发现了比例后,就可以运用比例的知识去解释一些现象甚至解决问题,当然这需要我们更深入的学习才行,今天我们只是初步认识比例的意义,更多的数学奥秘还等着咱们一起去探索。
[意图与思考:这个环节有的老师可能觉得应该前置到“环节四:师生交流深入学习”中,因为毕竟是学生都不会的问题,应该在前面的全班讨论中一并解决。其实不然,主要原因是:前几个知识点是本课的重点与核心,是学生本课应知、应会的,而“比例有什么用”这个内容是知识的拓展,在后续的教学中还将予以重点讨论,这里的学习只是让学生看到数学的应用价值,同时尝试用数学的眼光观察世界。另一方面,由于这一内容有趣、有挑战,在课末,仍然能吸引学生的学习注意。此外,更多老师教学时会将这一板块作为教学引入的情境,让学生从图中找到数据,写出比,再通过计算,发现两个比的比值相等,而后揭示比例的概念。笔者更倾向于将这一环节放在课的最后,因为让学生先掌握比例,再用比例的眼光看生活中的现象,这样的学习更有挑战性,且教学重点内容放在课前最黄金的学习时段,将有利于提高教学的实效。值得一提的是,在本环节的教学过程中,教师较少组织学生互助学习,师生的共同思考成了本环节学习的主要方式。教学方式的选用不应当也不可能是简单机械的。倡导什么不意味着只施行什么,因地因时选择合适的教学方式或许才是最好的方式。]

