直面疑惑排除矛盾——两次试教“平行四边形的面积”的思考

◇刘　颖　陈克胜

“探索活动：平行四边形的面积”是北师大版教材五年级上册第四单元“多边形的面积”中的内容，它是在学生掌握了面积概念、长方形面积计算、长方形特征以及用数方格等方法比较图形面积大小的基础上进行教学的。怎样使学生在原有知识经验的基础上，探索出平行四边形的面积计算公式，是本节课要解决的问题。

在教学中，我们多次进行教学尝试，力求最大限度地暴露学生的疑惑，使学生排除矛盾，解决问题，从而探究出平行四边形面积的计算公式。

一　大胆猜想，暴露疑惑

教材给出的情境如图1所示：

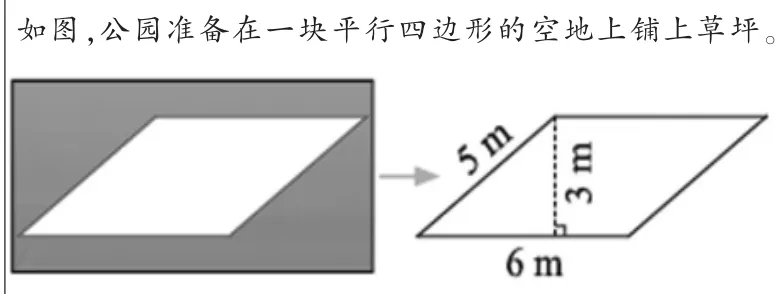
图1

同时，提出第一个问题：如何求这块空地的面积？说一说你的想法和理由。

提出这个问题的目的是借助学生已经学习过的长方形面积，鼓励学生猜想平行四边形的面积该如何计算，为此，我们采用了以下的教学措施：

第一次试教片段：

师：为了美化城市环境，市政的工作人员准备给一些空地铺上草坪，（图略）你能求出这块长方形空地的面积吗？

生：可以利用长方形面积公式求出草坪的面积是多少。

师：除了用公式计算平面图形的面积，我们还可以用什么方法求出图形的面积？

生：数方格的方法。

师：不错，是一种好方法。（出示图2）你能想办法求出这块平行四边形空地的面积吗？请同学们拿出学具袋和任务单（装有一个平行四边形和一张透明的方格纸），认真完成任务单中的探索（一）。

图2

探索（一）的题目是这样的：

你通过（ ）的方法得出平行四边形的面积是（）m2的。

师：谁来说说自己研究的结果？

生：我通过数方格得出平行四边形的面积是18m2。

（PPT动态演示数方格，师生交流数方格方法，确定结果）

师：（如图1）经过测量，我们发现这个平行四边形的底是6m，邻边是5m，底上的高是3m，平行四边形的面积18m2与测量所得的数据有何联系呢？请你试着大胆猜想一下。

通过数方格的方法学生已经知道平行四边形的面积是18m2，在猜想18与测量所得数据有何联系时，学生会自动排除6×5，即底×邻边这一类型和其他类型的例子，大多数学生立马会猜想到6×3，即底×高这一类型。乍一看结果很喜人，学生既得到了表扬，老师又得到了想要的结果。但深思后不难发现，本应该暴露在课堂上的种种猜想却不见了，特别是在分析学生的作业情况后，发现有不少学生仍将隐藏在头脑中“长方形的面积=长×宽”负迁移到平行四边形的面积计算上。

第二次试教片段：

教师在引入题目后，对学生的学具及探索活动中的题目进行了调整。

师：（出示图2）你能想办法求出这块平行四边形空地的面积吗？请同学们拿出学具袋和任务单，认真完成任务单中的探索（一）。

出示小组合作要求，其中学具袋中的学具大致有以下两类：一类是有一个标有底边、邻边和高的长度的平行四边形和一张透明的塑料方格纸；另一类是只有一个标有底边、邻边和高的长度的平行四边形。

探索（一）的题目是这样的：

你是通过（ ）的方法得出平行四边形的面积是（）m2的；利用图中所给数据，请你试着大胆猜想平行四边形的面积可能怎样进行计算。

经过这样的改动，学生的方法大致出现了以下五种：

①用数方格的方法得出平行四边形的面积是18m2；

②用算式6×3得出面积是18m2；

③用算式5×6得出面积是30m2；

④用算式3×5得出面积是15m2；

⑤把“周长”（6+5）×2=22（m2）理解成“面积”。

通过不同结果的对比，学生的思维发生激烈碰撞，学生把焦点聚在一个问题上：同样的平行四边形，怎么有这么多种答案？究竟哪种才是正确的呢？

建构主义学习理论告诉我们：学习不是被动接受信息刺激，而是学习者根据自己的经验背景对外部信息进行主动地选择、加工和处理，从而获得自己的意义的过程[1]。在交流中，学生发现用数方格的方法得出的平行四边形面积是正确的，进而可以排除邻边×邻边得出的数据，最后得出用6×3求得的平行四边形的面积有可能是对的。为下面的学习埋下了伏笔。

二　辩证分析，直面疑惑

在实际的教学过程中，往往有部分老师利用猜想6×3等于18就无意识地表露出这种列式计算是正确的，从而获得结论是底×高。仔细思考，虽然6×3=18从最后的结果来看是对的，但缺少了一些必要的辩证环节：我们只能说用列式6×3计算平行四边形的面积有可能是对的。故在经过上一环节后，我们的教学作了如下安排。

在讨论中，学生意识到6×3=18这种列式得出的面积数据是正确的，经过分析得出这里的6指的是平行四边形的底，3指的是平行四边形的高，进而学生猜想得出平行四边形的面积有可能等于底×高。但这仅仅是通过一个平行四边形的面积猜想得出的，不能肯定地得出平行四边形的面积=底×高，至此，“是不是所有的平行四边形的面积都能用底×高来计算呢”这个问题的提出，将本节课推上高潮。

教学片段：

师：我们发现列式18=6×3求解平行四边形的面积有可能是对的，这里的6指的是平行四边形的什么？3指的是平行四边形的什么？

生：这里的6指的是平行四边形的底。

生：这里的3指的是平行四边形的高。

师：平行四边形的面积有可能怎么算？

生：我猜平行四边形的面积=底×高。

其他学生点头表示同意。

师：是不是所有的平行四边形的面积都可以用底×高来计算呢？如何来验证我们的猜想呢？请同学们拿出学具袋，小组合作，验证你们的猜想。

学生动手操作，老师巡视指导，而后进行全班汇报。

汇报提纲：

①为什么要把平行四边形转化成长方形？

②如何把平行四边形转化成长方形？

③为什么都要沿着高剪开？（形成直角）

④拼成的长方形的面积与原来平行四边形的面积之间有什么关系？

⑤平行四边形的底和高与转化后的长方形的长和宽有什么关系？

师：想一想，我们为什么要把平行四边形转化成长方形？

生：要用学过的图形面积研究新的图形面积。

师：非常好的思路！在转化的过程中，平行四边形发生了什么变化？

生：平行四边形的面积没有变。

师：拼成的长方形的面积与原来平行四边形的面积之间有什么关系？

生：长方形的面积=平行四边形的面积。

师：平行四边形的底和高与转化后的长方形的长和宽有什么关系？

生：转化后长方形的长相当于平行四边形的底。

生：转化后长方形的宽相当于平行四边形的高。

生：这样就可以利用长方形面积公式，得到平行四边形的面积公式是底×高。

最后，教师鼓励小组合作验证平行四边形的面积=底×高，并反过来再利用公式平行四边形的面积=底×高，验证6×3列式是正确的，学生心中的疑惑就全部解开了，教学效果也随之提升。

三　对比练习，理解疑惑

练习是一节课的重要补充，目的有二：一是夯实学生的基础知识和基本技能；二是深化学生的思维，以有利于今后的发展。在练习中，我们既要适当体现课堂中学生暴露出的疑惑，也要体现一定的层次性、灵活性和深刻性。

为了体现层次性，我们设计了三个层次的练习。

第1题为基础练习，目的是考查学生对平行四边形面积的掌握程度，第（1）题给出底和底边上的高，第（2）题给出底和对边上的高。（如图3）

1.计算下面平行四边形的面积。

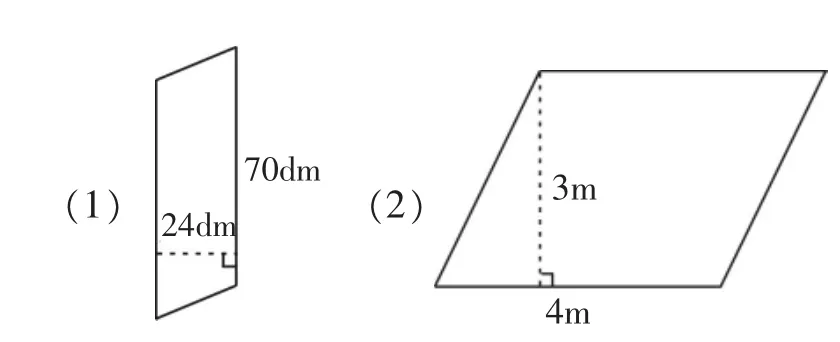
图3

第2题为巩固提高题，目的是通过对比练习使学生明确平行四边形面积计算公式中的底和高是对应的。在设计过程中，为了兼顾灵活性，特将此题题型设置为选择题。

2.请你判断。[2]

（1）下面哪个平行四边形的面积是3×4=12（m2）？

（2）计算下面图形的面积，哪个算式是正确的？（如图4）

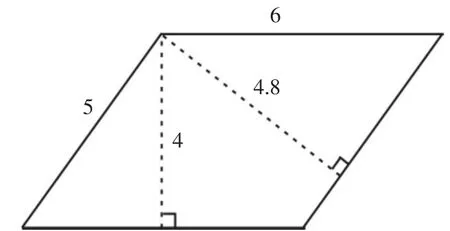
图4

A.6×4B.5×4.8C.6×4.8D.6×5

第3题为拓展应用题，考查学生综合运用平行四边形面积和周长相关知识解决问题的能力，同时也体现了一定的深刻性。

3.有一块平行四边形的菜地（如图5），如果在它的四周围上篱笆，篱笆的总长度是多少？

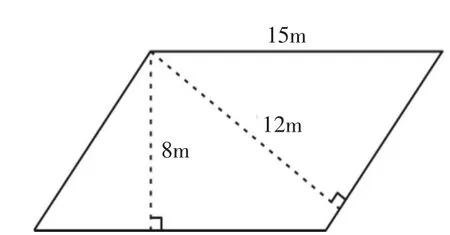
图5

参考文献：

[1]斯苗儿，朱国荣，顾志能，袁晓萍.教学，当直面学生的疑惑——关于“平行四边形的面积”一课所思所行[J].小学数学教育，2015（1/2）.

[2]张冀文.“平行四边形的面积计算”教学实录与设计意图[J].小学教学参考·数学，2009（7）.