一节高观点支持下的数学课

◇周卫东

为齐华的课堂写过多篇评析，整体感觉到：他的课堂越发清新隽永，越发深刻精到，越发广阔恢弘。看完“分数的意义”这则课例，使人油然而生“登高壮阔天地间，大江茫茫去不还”的诗意感。

“分数的意义”（或称“分数的再认识”）一课，历来是教学研究的热点课题，随堂课、研讨课、比赛课……多年来，同行们努力从不同的视角、用不同的方式诠释着对这一内容的理解。

但是，这一内容并不好教。究其原因有三：一是知识点较多，诸如单位“1”、分数的意义、分数单位等，附加不同教者在理解这一内容时的一些“增殖”目标；二是内容较为抽象，本课教学正逐步摆脱对具体素材的依附，把之前对分数的初步认识进行“数学化”提炼，形成纯理论的表达；三是时间跨度较大，苏教版教材分别在三年级上册、三年级下册两次安排了“分数的初步认识”的学习，而“分数的意义”的学习则安排在五年级下册，离前两次相关内容的学习已有了一年半之久。

应该说，齐华是一位善于啃“骨头”的人，而且越是“难啃的骨头”他越是能啃出味道、啃出精彩来！“分数的意义”的教学就是一例。

一 高视角

长期以来，教师对单位“1”的理解大多局限于教材，从文本的逻辑出发，依次呈现“一个物体”“一个计量单位”“多个物体”三种素材中具体分数的含义，然后进行统整、提炼、抽象，揭示：“无论是一个物体、多个物体，还是一个计量单位，都有一个共同的名称，就叫单位‘1’，通常用自然数‘1’来表示。”随后通过大量的实例进行巩固、强化。这样的教学被教师们高度认同且由来己久，似乎没有多少人能“跳出如来佛的掌心”。

数学有一种“自我生长”的力量，客观、冷峻、抽象、严密，它不依靠人类的探索，而是一直在那里，等着被发现。“微风人独立，蓦然一回首”，这是数学发现的写照。齐华就是一个善于发现的人。课堂的开始部分就呈现出别具一格、耳目一新的画面：出示6个同样的小正方形，并引发思考，“这些小正方形可以用什么数来表示呢？”在此 “问题场”中，激活学生的思维，学生通过合理想象，在充分的讨论、争辩中，形成“6个正方形可以用任何数来表示，关键看我们把多少个正方形看成‘1’，‘1’变了，这些正方形表示的数也就变了”的共识，从而理解了关于单位“1”的含义。继而，通过一幅图的多维解读，让学生理解：整数就是单位“1”的叠加，有几个单位“1”，就可以用整数几来表示；如果不满1个单位“1”，或者比几个单位“1”还多一小部分时，就用分数来表示。

这样的教学，使单位“1”跳出了一般化定义，犹如一把“尺子”，成为一个被比的标准，在“度量意义”的视角下被赋予了更深层的含义，充分体现了分数的一个最重要内涵，即它的无量纲性。

二 宽界面

如果说齐华看待教材的内涵有着“高视角”的眼光，那么，他在教学内容外延的拓展上，更有着异于一般人的“宽界面”特征。

再比如，课堂的最后部分，让学生围绕“刚才我们只是在数轴上找到某一个分数的位置，试想一下，如果我们把这几个不同的分数在同一条数轴上表示出来，你有什么感觉”的持续思考、对比，渐次感受到 “有点乱”“有点麻烦”“因为分数有着太多的分数单位，从而给我们的比较、计算、解决问题等带来很大的麻烦。所以，日常生活中，分数离我们越来越远”等关于分数的不足，促使学生在分数与小数的比较中进一步感受分数的特点，并进而形成“我们生活的世界，遵循着优胜劣汰的原则……好在，人们逐渐认识到分数的这一缺点，又对分数进行了一些改造，并发明了一种全新的数。这一内容，我们将在后面的学习中继续来研究”的学习心向和学习需求。

三低结构

新形势下，数学课堂呈现出低结构活动的特点：注重联系，关注结构；强调过程，淡化结果；突出可选择性与可生成性……这也正是基于“培养全面发展的人”的总体目标对课堂教学提出的全新要求。齐华的课堂正朝向这个方向逐渐地改变。

这节课突出了对分数含义的多元表征。不囿于教材上的标准定义“把单位‘1’平均分成若干份，表示这样的1份或几份的数，叫作分数”，而是基于经验，顺着学情，让学习“向四面八方打开”，引导学生从 “用文字表示”“画图表示”“用数轴表示”“用分数单位表示”等不同的侧面对分数的含义进行诠释与表达。

这节课突出了学习过程的结构化形态。很欣赏这节课的板书（如图1），此板书以思维导图的方式呈现学习过程，让学生感受到：学习素材之间是有联系的，学习方式与学习内容之间是有联系的，数和形之间是有联系的，形式与本质之间是有联系的。

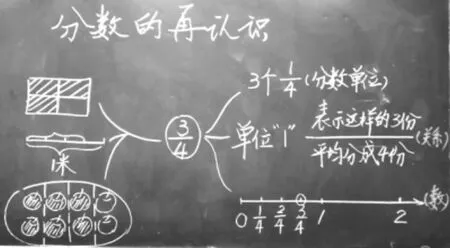
图1

行文至此，我翻开与齐华的QQ聊天记录：“我请你评课，是知道你对这节课有深入思考。”“评课不是找赞歌，是求深解。”这样的话打动了我心中那最柔软的部位，让我敬佩他实事求是、服膺真理的精神。

齐华说得没错，对“分数的意义”的教学，我做过一些研究。仔细研读齐华的这则课例，在敬佩他求深、求广、求新等研究精神的同时，也感觉到本课的一些缺憾，其中最明显的就是：这节课承载的目标显得稍多。该课有五个部分，与一般教学相比，增加了诸如“分数可以表示一个具体的数”“分数的许多不足之处”等教学目标，而这些深层次目标，要想让学生清楚、明白并进而达到理解、通透的水平，显然不是在一两个课时内所能解决的。我非常认同约翰·D·布兰思福特在《人是如何学习的》（P.18）一书中的观点：“必须用少量主题的深度覆盖去替换学习过程中对所有主题的表面覆盖，这些少量主题使得一些关键概念得到理解。”我们不妨适当地降低重心，俯就儿童，减轻负载，在数学与儿童之间找到一个适切的坐标，朝向儿童发展的“可能性”，一步一步地迈近。