设计梯度，层次教学

魏菊

[摘 要] 受多种因素的影响，不同的学生数学的学习效果必然不同. 准确意识到学习差异的存在，从实际角度关注教学现状，做出最为适合学生的有效设计，由学习差异入手，开展有梯度、有层次的课堂教学是非常关键的，对于提升高中数学教学实效是至关重要的.

[关键词] 差异；认知；处理

高中数学的学习效果受到很多因素的影响，除了来自教师方面的教学方式之外，学生本身作为学习活动的主体，也在发挥着更为重要的影响作用. 每个学生都是独立的个体，他们的思维水平、知识基础与接受能力之间都存在着较为显著的差异. 在这样的差異作用之下，每个学生面对不同的知识内容，学习的效果必然也是不同的. 对于高中数学的整体教学效果来讲，这一因素的影响是很大的. 因此，准确意识到学习差异的存在，并正确处理学生之间的学习差异，对于提升高中数学教学实效来讲是至关重要的.

[?] 为教学目标设计梯度，分层次做好学习准备

每个知识模块学习展开之前，教师都会为学生设计相应的学习目标，作为整次教学活动的方向指引. 在目前的教学过程当中，教师大多会将学习目标进行统一设计，这无形当中便为所有学生提出了相同的学习要求. 这种做法并不够科学合理. 既然每个学生的知识能力状况都不一样，接受新知识的效果自然也是不同的. 让存在学习差异的学生达成相同的学习目标，显然是不现实的. 由此，为学生设计出层次化的教学目标，便成了教学优化的第一步.

例如，在为概率统计的内容设置教学目标时，笔者通过一道分层题目予以展现：

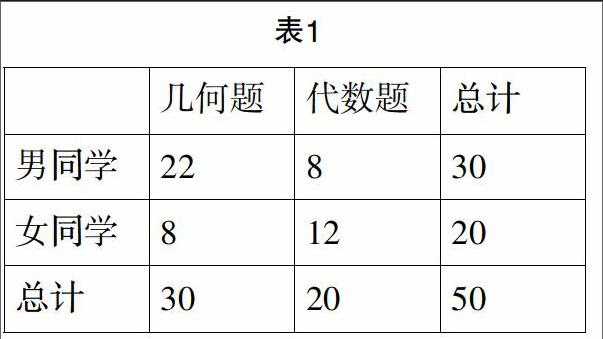
某研究小组的学生猜想，由于性别差异所决定的思维方式不同，男生与女生在解答几何题与代数题时的能力也是不同的. 为此，他们以分层抽样的方式抽取了30名男生与20名女生，对他们解答相同的一道几何题与一道代数题的结果进行了统计，结果如下表（单位：人）.

（1）通过分析表格中的数据，能不能将解答不同问题的能力与性别差异有关的概率确定为97.5%？

（2）若小张用5～7分钟的时间解答一道几何题，小李需要用6～8分钟，那么，二人分别解答同样一道几何题，小李比小张解答速度快的概率是多少？

两个问题中不仅呈现了不同的知识内容，更揭示出了不同层次的能力要求，这也为学生提供了灵活的学习目标选择空间.

为教学目标设计梯度，为层次教学开了一个好头. 这让学生从学习开始之初便得以寻找到一个适合自己的平台高度. 笔者认为，对于高中学生来讲，最合适的学习目标应当确定为“踮踮脚，够得着”的高度. 这样既不会浪费学生的学习精力，也不会对学生造成过大的心理压力. 分梯度的目标设计，让差异化的学生找到了相应的学习方向，接下来的学习活动自然开展得更加有的放矢.

[?] 为课堂教学设计梯度，分层次呈现知识内容

课堂教学作为高中数学教学的主体部分，自然也成了层次教学铺开的主战场. 根据知识内容各自的重点与特点，教师往往会选择不同的教学方法. 这也决定了，层次教学的处理会随着教学方法的变化而有所不同. 无论具体情况如何，教师只需要把握住这样一个总体原则：让每一个学生都能够适应课堂，在自己现有的知识基础上，最大化地扩充知识版图.

例如，集合常常被学生认为是比较基础和边缘的内容，不会投入过多关注，然而想要将这部分内容的分数稳稳拿住，也不是那么容易的. 在对这部分知识进行教学时，笔者也采取了层次教学的方式来突出教学重点：现有集合A={x

-2≤x≤5}，集合B={x

m+1≤x≤2m-1}.

（1）若A∩B= ，则m的取值范围是什么？

（2）若A∪B=A，则m的取值范围是什么？

表面看来，这两个问题之间是并列的关系. 但是，真正解答起来便会发现，其中包含了一个从知识内容到思想方法的阶梯性延伸. 在分析上述问题的过程当中，学生首先需要运用基础知识，准确理解已知条件的含义，再运用分类讨论的思想方法，将每一种情况分析周全，方能得到正确答案. 层次化的问题设置，也让学生看到了集合知识学习的全部落点.

有的教师会认为，将知识内容分梯度地呈现出来，会造成教学内容的不完整. 这是一个思想误区. 对于任何一个部分的知识内容，我们都会为之设定从基础到拔高的教学要求. 只要教师把基础要求作为层次教学的初始，以之开始向更高要求逐步延伸，就完全可以让课堂教学保质保量. 这也让学生在接触知识时得以更加全面地看到其所能达到的下一个高度，从而为下一步深入学习做好准备.

[?] 为作业布置设计梯度，分层次重温课堂所学

对于高中数学教学来讲，课后作业不仅是对课堂所学知识的重温与巩固，更是对知识能力进行拓展延伸的绝佳机会. 因此，课后作业的布置必须得到教师的普遍重视，更要将层次教学的理念渗透到作业设计当中去. 具体说来，就是在同一道习题当中多设几问，将问题难度细化、分开.

例如，在完成了线面关系内容的课堂教学后，笔者为学生布置了这样一道作业习题：

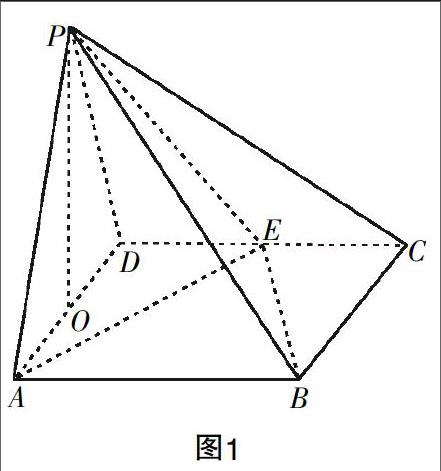
如图1所示，在四棱锥P-ABCD中，平面ABCD是一个正方形，平面PAD是一个等边三角形，且两个平面相互垂直，点O和点E分别是AD边和CD边的中点，且AD边长为2.

（1）求证：OP⊥平面ABCD；

（2）求二面角P-BE-A的余弦值；

（3）若要让线段PM与平面PAD成30°角，能否在线段AB上找到这样的点M？

在这三个问题的设计中，笔者有意识地从知识深度上拉开了梯度：先是引导学生调动线面垂直的知识解题，然后引出难度稍有增加的二面角的内容，最后则是线面关系的开放性问题. 这一连串问题思考下来，学生对于线面关系的理解不知不觉地走到了一个新高度，并让不同学习效果的学生都找到了自己需要努力的方向.

实际上，分层次的作业设置，并不需要教师将原有的作业题目推倒重来，而是只要选择重难点问题进行重新优化即可. 特别是对于一些难度较大的作业题，教师可以按照问题分析的思维路径，在同一个方向上由浅入深地多提几个问题，让问题之间形成难度阶梯，并引导学生逐步走向预设的思维深度. 这样一来，既实现了分层布置作业的效果，还为学生解答难题提供了辅助.

[?] 为阶段测试设计梯度，分层次检验知识效果

除了必要的期中、期末考试之外，平时学习中的阶段测试也是高中数学教学有效开展的必要保证. 在以往的教学当中，教师往往会对阶段测试的检验功能更加关注，其实，如果能够在阶段测试中体现出层次教学的特点，对于知识教学效果来讲会是一个无形的二次推动.

例如，在立体几何章节的阶段测试当中，笔者特意设计了这样一个问题：

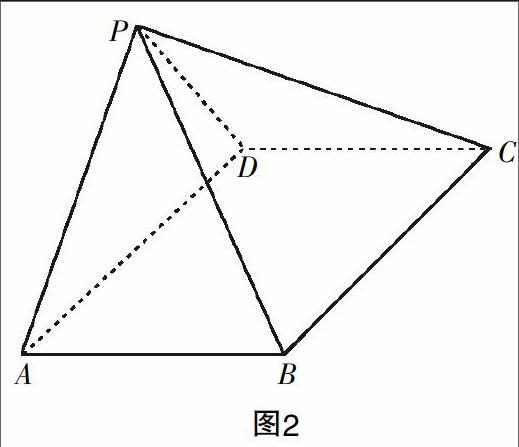
如图2所示，在四棱锥P-ABCD中，底面ABCD是一个矩形，且平面PAD与底面ABCD垂直.

（1）求证：AB⊥PD；

（2）若∠BPC是一个直角，且PC的长为2，PB的长为，现欲使得四棱锥P-ABCD的体积达到最大，应当将AB的長度确定为多少？此时，平面CPD与平面PCB之间所形成的夹角的余弦值是多少？

这两个问题的设定，很清晰地体现出了测试当中的考查要点. 第一个问题只对线线垂直这个基本内容进行了考查，第二个问题则是从点、线、面的关系以及最值确定等内容的综合角度进行了考查. 两个问题的逐次安排，从内容数量和知识难度的角度都呈现出了明确梯度，在层次鲜明的设定之下，知识检验效果也更为利落了.

对于高中数学教学来讲，阶段测试就像是一种无声的语言，蕴含着教师对学生提出的学习要求. 学生当前应当将知识内容掌握到何种程度，从测试当中的问题难度设置就可以看得出来. 因此，分层次地设计测试问题，实际上就是在分层次地对学生提出学习要求. 这样区分能力特点设计出的阶段测试，往往能够在分层次的过程中收获最佳知识检验效果.

综上所述，为了从实际角度关注教学现状，做出最为适合学生的有效设计，由学习差异入手，开展有梯度、有层次的课堂教学是非常关键的. 这样的做法，不仅能够为不同学习能力状态的学生提供相应的思维平台，让数学教学效果渗透到每个角落中去，更能够让课堂教学更具层次深度，让知识学习过程愈发立体. 通过较长一段时间的层次化教学实践，作者明显看到了学习效果所呈现出的优化幅度. 希望更多教师能意识到这个教学侧面，并通过其将数学课堂打造得更加完善高效.