基于子集模拟的埋地管道失效概率评估*
骆正山,李 娇
(西安建筑科技大学 管理学院,陕西 西安 710055)
0 引言
管道的风险评价[1-4]是管道完整性研究中的1项重要内容,而管道定量风险评价的核心内容是对管道失效概率的评估和计算,失效概率的准确性对风险评价具有重要意义[5]。对于失效概率的计算目前国内外主要有3种计算模型:一是数据库分析模型。通过对失效信息的收集、统计和分析确定失效因素,欧美国家已建立较完备的数据库[6],但是目前国内管道失效数据库并不完善,难以对管道系统失效概率进行有效评估;二是故障树分析模型。张振兴等[7]通过建立故障树定性分析管道失效事件发生概率;汪长永等[8]利用模糊综合评价法对油气管道进行风险评价。但用故障树模型难以客观地确定权重,条件独立性检验的结果不可靠;三是结构可靠性理论模型。在失效数据库尚未完善的情况下使用结构可靠性模型计算失效概率是最有效和准确的[9],目前最常用的是一次二阶矩法和蒙特卡洛方法。柳春光等[10]利用一次二阶矩法对埋地管道的失效概率进行了分析;Rackwitz和Fiessler[11]在改进的一次二阶矩基础上对管道进行可靠性分析;Peter等[12]利用蒙特卡洛方法计算了管道失效概率;罗更生等[13]利用蒙特卡洛方法对管道在随机因素影响下的可靠性问题进行了分析。后2种方法均需要大量的随机抽样,计算量大且效率较低,在失效概率较小并出现高维问题时,缺乏1种通用的算法来计算埋地管道失效概率,因此迫切需要能准确有效地对埋地管道失效进行分析的方法。子集模拟[14-17]是1种针对小失效概率问题的方法,其基本思想是引入合理的中间失效事件,通过划分一系列具有序列包含关系的子集,将需要计算的小失效概率转化为较大的条件失效概率乘积形式,利用蒙特卡洛方法对条件样本点进行抽取,从而能估计大的条件失效概率。以下利用子集模拟计算可靠性的优点,建立了埋地管道失效概率模型,并对随机变量进行敏感性分析。
1 埋地管道失效概率模型
1.1 子集模拟的特点
对系统可靠性的分析问题而言,为了保证其运行安全,失效概率必须非常小。而对于结构系统的概率可靠性计算方法,蒙特卡洛模拟法是应用最广泛的,该方法对于可靠性评估问题适应性强,不需要失效域信息,并且对变量维数的变化不敏感,但其缺点是所需要的抽样数目过于庞大,计算效率非常低下。因此,引入一种能显著提高多维小失效概率问题计算效率的方法,即由AU等[18]发展的子集模拟方法(SS),通过引入合理的中间失效事件,将小概率问题转化为一系列较大的条件概率的乘积(图1)。

图1 子集模拟示意Fig.1 Subset simulation

1.2 埋地管道的失效模型
按照目前的ASME B31G标准,埋地管道系统的失效应力为:
(1)
式中:σ为材料流变应力,σ=σS+68.95(σS为管道材料的屈服强度,MPa);A为通过管壁厚度纵向平面的缺陷面积,A=0.85Ld,mm2;A0为未受损管道纵向面积,A0=Lt,mm2;t为壁厚,mm;d为腐蚀缺陷深度,mm;MT为Folias系数,它与腐蚀缺陷长度L,管道外径D和管道壁厚有关,即:
MT=
(2)
(3)
O’Grady T J II等[21]研究表明,在稳态下将腐蚀速率视为线性发展也是合理的。基于此假设,管道缺陷深度方向的腐蚀速率Rd=Δd/ΔT(mm/a),长度方向的腐蚀速率RL=ΔL/ΔT(mm/a),式中,Δd为2次测量缺陷深度的差值;ΔL为2次测量缺陷长度的差值;ΔT为2次检测时间的间隔。如果最后1次(T0)时刻检测到腐蚀深度和长度分别为d0和L0,则T时刻腐蚀的深度和长度分别为d(T)和L(T),即:
d(T)=d0+Rd(T-T0)L(T)=L0+RL(T-T0)
(4)
将式(4)代入式(3),则管道失效压力为:
(5)
1.3 基于子集模拟的管道失效概率模型

管道失效概率(Pf)可以基于管道失效过程中一系列故障域(或子集)来计算,即通过条件概率P(F1)和P(Fi+1|Fi)的乘积来计算管道失效概率Pf,如式(6):
Pf=P(Fm)=P(Fm|Fm-1)P(Fm-1|Fm-2)…P(F2|
(6)
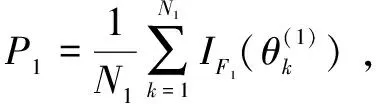
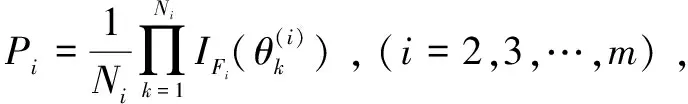
(7)
式(7)即可算出埋地管道总失效概率,Pf越小,则表示计算Pf时需要越多的随机变量样本,管道失效事件越罕见。但即使Pf很小,通过式(7)合理的选取中间失效区域{Fi:i=1,2,…,m-1},也可高效模拟出埋地管道的失效概率。如假定P(F1),P(Fi+1|Fi)≈0.1,i=1,2,3,则Pf≈10-4,对蒙特卡洛法来说Pf太小,计算效率低并且需要极大量的样本,但通过条件失效概率计算则很容易得到。可以看出,子集模拟方法在对埋地管道小失效概率问题计算上的高效性和便捷性。
1.4 基于子集模拟的参数灵敏度分析
对埋地管道进行可靠性灵敏度分析有助于计算出在埋地管道运行的过程中哪些随机变量对系统可靠性较敏感以及修改哪些随机变量的参数更有利于埋地管道的维护和保养。在上述分析的基础上使用子集模拟,Pf可以被转化为一系列条件失效概率Pi(i=1,2,…,m)。通过P1可以获得随机变量相对分布参数α(均值μ或者标准差σ)失效概率的偏导数。即所谓的可靠性敏感度,如式(8)所示:
(8)
通过分析可以反映出分布参数对于失效概率的意义。根据样本均值,其可靠性敏感度可以通过式(9)和式(10)得到:
(9)
(10)
2 实证研究
通过上述研究,收集数据对某埋地管道的失效概率以及随机变量进行模拟分析。根据可靠性理论,假设下列随机变量均服从正态分布,根据系统实际情况选取各随机参数的均值及变异系数,结果如表1所示。其中:k,n为腐蚀模型参数(腐蚀指数,腐蚀乘子);αp为膨胀系数;Δθ为温差;P,Ep分别为工作压力,弹性模量;vp,σs,Km,Ic分别为管道泊松比,管道屈服强度,弯曲弯矩系数,冲击系数;Kd,Bd,Cd分别为管道基座系数,沟槽宽度,土体荷载计算系数;σRL,χ,W,γ分别为最大残余应力,管道弯曲曲率,竖直载荷,土体重度。

表1 随机参数及分布
在任意1个模型中都包含多个失效事件会导致系统失效,由于在失效事件中存在共同的随机变量且失效模式都是相互关联的,因此对于管道失效预测要考虑整个系统。由失效模式之间的相关系数可知所有的失效模式都正相关,即埋地管道系统中失效模式可能会同时发生。因此,根据可靠性理论系统失效概率Pf,s可由式(11)计算:
(11)
式中:Pf,j为基于第j种失效模式的失效概率;r为系统中考虑到的失效模拟数量。
子集模拟最大的优势就是能够更有效的预测小失效概率,为验证子集模拟计算埋地管道失效概率的有效性,在Matlab中编制相应的计算程序,分别利用子集模拟与蒙特卡洛法计算失效概率,计算结果见表2。

表2 失效概率计算结果

图2 管道失效概率的变异系数Fig.2 Coefficients of variation of pipe failure probability
由表2可以看出,当失效概率的数量级很小时使用蒙特卡洛法是非常低效的,子集模拟仅需要少量样本就可以达到MCMC上万个样本的精度,伴随着精确性的提高也节省了大量的计算时间,研究表明相比MCMC,子集模拟的计算时间要节省67%。

利用子集模拟方法来对影响埋地管道系统失效概率的参数进行计算,确定各参数的重要性以便对影响因子较大的参数进行进一步分析。通过式(9)和(10)得到各随机变量对管道失效概率的不同影响程度。经计算得到在管道运行第10a时对失效概率影响最大的前5个因素,其对失效概率的灵敏度分布见图3。

图3 各参数灵敏度分布Fig.3 Distribution of parameters sensitivity
由图3可知,在埋地管道服役第10 a的随机参数中,工作压力、腐蚀速率、管道壁厚和屈服强度是对管道系统失效概率影响最重要的4个因素。
通过上述分析,已经得到了在管道运行的过程中对失效概率影响较大的参数,但是无法确定在管道整个服役过程中各随机参数是如何影响管道失效概率的,根据子集模拟计算方法在Matlab中编写程序进一步模拟埋地管道各随机参数在不同服役年限中对失效概率的影响,其模拟结果如图4所示。
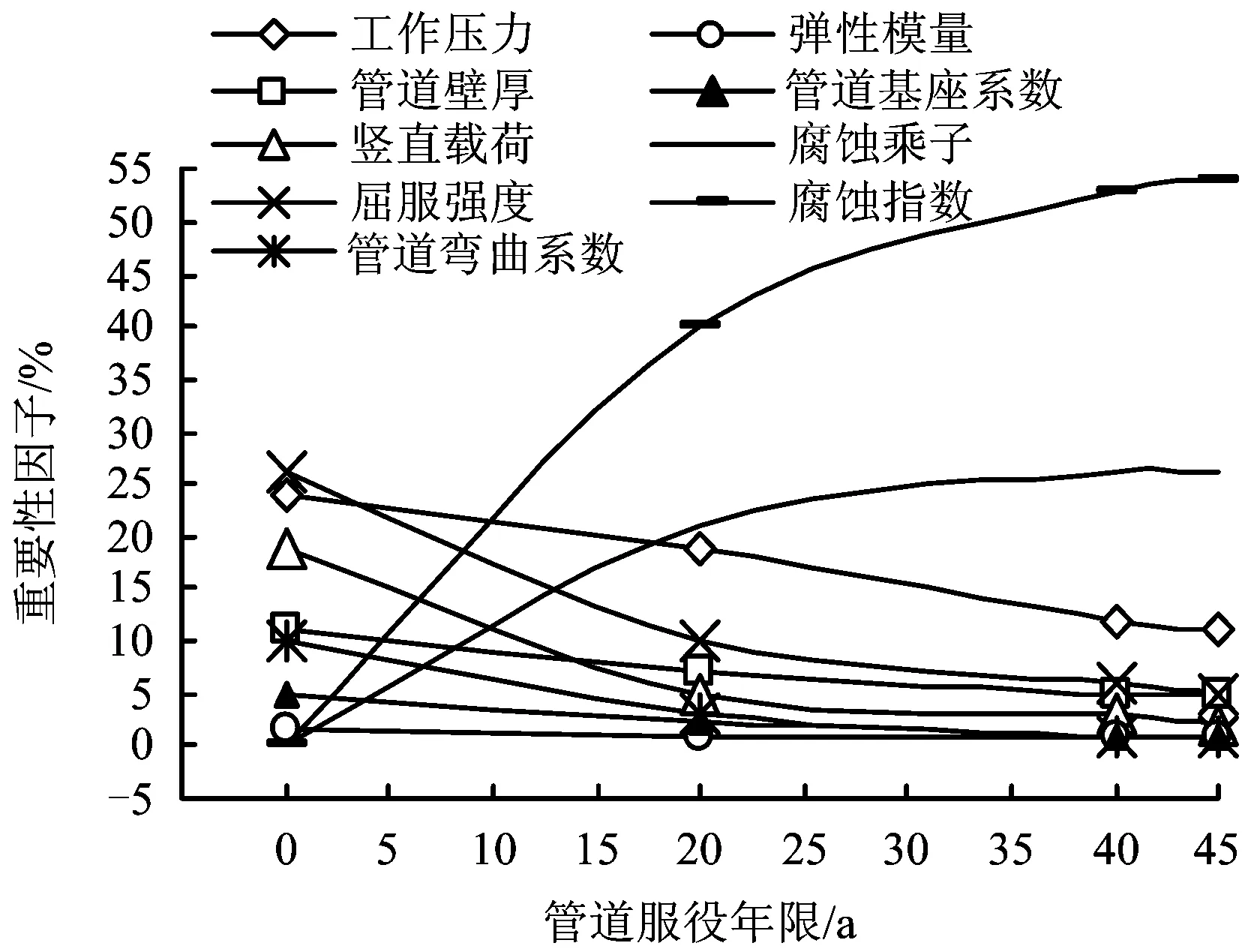
图4 埋地管道的随机参数重要性因子变化Fig.4 Variation of the importance factor of random parameters of buried
分析图4可得出如下结论:
1)随着埋地管道服役寿命的增加,屈服强度、管道壁厚、管道弯曲系数和竖直载荷这几个参数对系统失效概率的影响均呈降低趋势。
2)腐蚀在管道的运行过程中逐渐成为管道失效的主要影响因素。尤其在管道服役后期时,腐蚀因素对管道失效概率影响占到65%,而其余随机参数中除了工作压力外,均在9%左右。
3 结论
1)针对目前国内在确定埋地管道失效概率方面的主观评价法和不适于实际需求的模拟方法,根据系统小失效概率的特点引入子集模拟方法对埋地管道失效概率进行计算,经过试验模拟证明,采取子集模拟方法计算小失效概率在计算时间和效率上都有大幅度提高。
2)根据埋地管道系统的失效概率模型,推导出管道系统随机变量参数的偏导数,从而得到计算参数灵敏度的方法。在此基础上可以定量计算各随机参数对管道失效概率的影响情况,确定在管道运行过程中需要重点维护和监测的变量。
3)通过分析可以看出,在管道整个服役过程中,不同参数对失效概率的影响是大不相同的,在管道运行中期,对失效概率影响较大的主要是屈服强度、工作压力、竖直载荷以及管道壁厚;在管道运行后期,为了保证管道的安全运营应该重点对腐蚀情况进行监测和防护。
[1]姚安林,赵忠刚,张锦伟. 油气管道风险评估质量评价技术[J]. 天然气工业,2013,33(12):111-116.
YAO Anlin,ZHAO Zhonggang,ZHANG Jinwei. Quality evaluation for oil and gas pipeline risk assessment [J]. Natural Gas Industry,2013,33(12):111-116.
[2]张杰. 基于主成分-聚类分析法的管道风险评价方法[J]. 油气储运,2014,33(2):139-143.
ZHANG Jie.Pipeline risk assessment method based on principle component-clustering analysis[J].Oil & Gas Storage and Transportation.2014,33(2):139-143.
[3]胡翩,刘书海,王德国,等. 基于变权综合理论的天然气管道动态风险评价[J]. 中国安全科学学报,2012,22(7):82-88.
HU Pian,LIU Shuhai,WANG Deguo,et al. Dynamic risk assessment for natural gas pipelines based on variable weights comprehensive theory[J].China Safety Science Journal.2017,22(7):82-88.
[4]冯云飞,孟繁博,朱富斌,等. 基于灰色层次分析法的长输管道风险评价[J]. 油气储运,2013,32(12):1289-1294.
FENG Yunfei,MENG Fanbo,ZHU Fubin,et al. Risk assessment of long-distance pipeline based on gray analytic hierarchy method[J].Oil & Gas Storage and Transportation.2013,32(12):1289-1294.
[5]俞树荣,李建华,李淑欣,等. 埋地管道腐蚀剩余寿命预测概率模型[J]. 中国安全科学学报,2008,18(6):11-15.
YU Shurong,LI Jianhua,LI Shuxin,et al. Probability model for the prediction of corrosion remaining life of underground pipelines[J].China Safety Science Journal,2008,18(6):11-15.
[6]Young DY,Jong BA. A method of quantitative risk assessment for transmission pipeline carrying natural gas[J].Journal of Hazardous Materials,2015,123(1):1-12.
[7]张振兴,成庆林,孙巍. 基于FTA的输油管道凝管失效可能性研究[J]. 化工设备与管道,2015,52(5):58-61.
ZHANG Zhenxing,CHENG Qinglin,SUN Wei. Research of failure probability of congelation in oil pipeline based on FTA[J].Process Equipment & Piping,2015,52(5):58-61.
[8]汪长永,杨卫,殷焕召,等. 模糊综合评价法在油气管道跨越工程风险评价中的应用[J]. 中国安全生产科学技术,2010,6(3):143-146.
WANG Changyong,YANG Wei,YIN Huanzhao,et al. Application of fuzzy comprehensive evaluation in risk evaluation in risk evaluation of pipeline crossing engineering[J].Journal of Safety Science and Technology.2010,6(3):143-146.
[9]李军,秦朝葵,马洪敬. 城市高压燃气管道的结构可靠性分析[J]. 中国安全生产科学技术,2014,10(11):113-118.
LI Jun,QIN Chaokui,MA Hongjing. Analysis on structural reliability of urban high-pressure gas pipeline[J].Journal of Safety Science and Technology.2014,10(11):113-118.
[10]柳春光,冯晓波. 连续埋地管线沉陷情况下可靠度分析[J]. 大连理工大学学报,2011,51(4):581-586.
LIU Chunguang,FENG Xiaobo. Reliability analysis of continuously buried pipeline subjected to settlement[J].Journal of Dalian University of Technology.2011,51(4):581-586.
[11]Rackwita R,Flessler B.Structural reliability under combined ranfom load sequences[J].Computers&Structures,1978,9(5):489-494.
[12]Carr P.Riser and Pipeline Corrosin Risk Assessment[C]//Offshore Technology Conference Asia. 2014.
[13]罗更生,周煜. 含裂纹油气管道可靠性评定方法及敏感性分析[J]. 石油学报,2011,32(6):1083-1087.
LUO Gengsheng,ZHOU Yu. A reliability assessment method of crack-containing oil-gas pipelines and its sensitivity analysis[J].Acta Petrolei Sinica.2011,32(6):1083-1087.
[14]宋述芳,吕震宙. 基于马尔可夫蒙特卡罗子集模拟的可靠性灵敏度分析方法[J]. 机械工程学报,2009,45(4):33-38.
SONG Shufang,LYU Zhenzhou. Structural reliability sensitivity analysis method based on Markov Chain Monte Carlo subset simulation[J].Journal of Mechanical Engineering,2009,45(4):33-38.
[15]张曼,唐小松,李典庆. 含相关非正态变量边坡可靠度分析的子集模拟方法[J]. 武汉大学学报(工学版),2012,45(1):41-45,53.
ZHANG Man,TANG Xiaosong,LI Dianqing. Reliability analysis of slope stability involving correlated non-normal variables using subset simulation method[J].Engineering Journal of Wuhan University,2012,45(1):41-45,53.
[16]房冠成,吕震宙,魏鹏飞. 结构系统可靠性及可靠性灵敏度分析的改进子集模拟法[J]. 航空学报,2012,33(8):1440-1447.
FANG Guancheng,LYU Zhenzhou,WEI Pengfei. Modified subset simulation method for reliability and reliability sensitivity analysis of structural system[J].Acta Aeronautica et Astronautica Sinica,2012,33(8):1440-1447.
[17]薛国峰,王伟,赵威. 基于多点Metropolis的子集模拟方法[J]. 哈尔滨工业大学学报,2011,43(S1):120-125.
XUE Guo-feng,WANG Wei,ZHAO Wei.Subset simulation methods based on Multiple-Try Metropolis[J].Journal of Harbin Institute of Technology,2011.43(S1):120-125.
[18]AU S K,BECK J L. Estimation of small failure probabilities in high dimensions by subset simulation[J]. Probabilistic Engineering Mechanics, 2001,16(4):263-277.
[19]徐瑞,张加兴,苏成. 非平稳随机激励下结构动力可靠度时域显式子集模拟法[J]. 工程力学,2013,30(7):28-33,39.
XU Rui,ZHANG Jiaxing. SU Cheng. Time-domain explicit formulation subset simulation method for dynamic reliability of structures subjected to non-stationary random excitations[J].Engineering Mechanics,2013,30(7):28-33,39.
[20]刘佩,姚谦峰. 基于子集模拟法的非线性结构动力可靠度计算[J]. 工程力学,2010,27(12):72-76.
LIU Pei,YAO Qian-feng.Dynamic reliability computation for non-linear structures based on subset simulation method[J]. Engineering Mechanics,2010,27(12):72-76.
[21]O’Grady T J II,Hisey D T,Kiefner J F.Pressure calculation for corroded pipe developed[J].Oil and Gas Journal.1992,90(42):64-68.

