加性噪声下增广容积卡尔曼滤波及其目标跟踪应用

刘 江 叶松庆

(中国科学院重庆绿色智能技术研究院 重庆 400714)

加性噪声下增广容积卡尔曼滤波及其目标跟踪应用

刘 江 叶松庆

(中国科学院重庆绿色智能技术研究院 重庆 400714)

传统容积卡尔曼滤波(CKF)有良好的滤波精度和较低的计算复杂度，使其广泛被应用于目标跟踪系统。但在高维非线性和波动性大的目标跟踪系统中，3阶和高阶CKF分别存在滤波精度不足和稳定性低的问题。为提高CKF的滤波精度并保证稳定性，讨论和给出加性噪声下的增广容积卡尔曼滤波(ACKF)。在仿真中，将CKF、UKF和ACKF应用于5维高非线性目标跟踪，并分析比较三者的目标跟踪性能。研究结果表明，在高维非线性目标跟踪系统中，3阶ACKF可以获得更好目标跟踪精度和稳定性，以及可接受的计算复杂度。

目标跟踪 增广容积卡尔曼滤波 非线性滤波 加性噪声

0 引 言

因为卡尔曼滤波(KF)具有良好的鲁棒性和最优特性[1-2]，它被广泛地应用于线性系统的状态估计和目标跟踪领域[3-4]。但对于非线性系统，经典卡尔曼滤波存在局限性。对此研究人员提出扩展卡尔曼滤波(EKF)，使其较好地适用于低维和低非线目标跟踪性系统[5]。但对于高维和高非线性系统，EKF会导致严重的系统失真和滤波误差。针对这类目标跟踪系统，研究人员对粒子滤波(PF)在移动物体跟踪系统中的应用进行了研究，并做了相关性能分析[6-8]。粒子滤波通过大量的随机样本和归一化权重对非线性系统的状态分布进行逼近，故粒子滤波存在计算复杂度高，滤波精度低和数值发散等缺点[9]。为解决这些问题，Julier等人[10]提出基于无迹变换(UT)的无迹卡尔曼滤波(UKF)。UKF通过UT变换和矩匹配获得确定性样本和权重，具有良好的滤波精度和较低的计算复杂度。相比于粒子滤波，UKF在非线性目标跟踪系统中有一定的性能优势[11-12]。UKF的滤波精度取决于UT变换所计算的均值和协方差。为提高UKF的滤波精度，人们提出了高阶UT变换[13-14]、新型Sigma集合[15]以及线性扩展形式的UKF[16]。以上提高UKF滤波精度的方法，均以修改样本集合或样本数量为目标。但Wu等人[17]从系统本身出发，讨论了UKF在加性噪声下的增广UKF(AUKF)，并对比分析AUKF和UKF的性能。研究结果表明，AUKF能比UKF更好地匹配奇数阶矩信息，并在非线性滤波中获得更好的滤波精度和稳定性。但为使样本和权重能匹配状态的4阶矩，UKF参数可能为负数[18]。当系统维数时，UKF在均值点上样本权重为 。该负权重可能致UKF的不稳定性[19]。在AUKF中，系统状态的维数增广后使得该不稳定性问题更加明显。

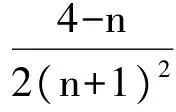
对比UKF和CKF，两者具有很高的相似性[21,28]。尤其是当UKF尺度因子κ=0，此时UKF与3阶CKF具有相同的样本点和样本权重[29]。根据AUKF的思想，Li等人[30]给出了加性噪声下增广CKF(ACKF)。3阶ACKF的样本点具有相同的正权重，且具有更好的滤波性能。

本文中，先对基于样本的卡尔曼滤波框架和球面-径向容积法则进行了总结，并给出3阶CKF的样本及其权重。然后给出一般形式下的增广球面-径向法则。基于此，讨论了增广形式的动态系统和测量方程，并给出ACKF的滤波流程。在目标跟踪仿真中，将UKF(κ=3-n)、3阶CKF、5阶CKF与3阶ACKF应用于5维的跟踪模型中，分析它们在目标的位置、速度以及角速度分量上的滤波性能。结果表明，3阶ACKF有更好的滤波性能，尤其是在非线性程度高的位置和速度分量上明显好于其他三种算法。因此3阶ACKF更适合于高非线性目标跟踪系统。

1 容积卡尔曼滤波算法

1.1 基于样本的卡尔曼滤波框架

卡尔曼滤波框架被广泛地应用于基于样本点的非线性滤波算法中。总结UKF和CKF，可知两者的区别主要在于样本选择策略和权重确定方法，但使用相同的卡尔曼滤波框架。因此，本节将对非线性卡尔曼滤波框架进行总结。

考虑如下非线性动态系

xk+1=f(xk)+vk

(1)

zk+1=h(xk+1)+wk+1

(2)

其中，xk∈n，zk∈m；vk和wk分别为互相独立的过程和测量高斯白噪声，协方差分别为Qk和Rk+1。

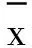
(3)

(4)

此时，基于卡尔曼滤波框架的非线性滤波过程如下：

(1) 时间更新

Si,k+1|k=f(Si,k|k)

(5)

(6)

(7)

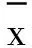
(2) 测量更新

(8)

(9)

其中，yk+1是测量值，以及：

(10)

(11)

(12)

(13)

(14)

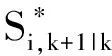
1.2 球面-径向容积法则

在CKF中，核心是通过球面-径向法则选择样本和权重集合，对一类积分I(f)=∫f(x)×exp(-xTx)dx的逼近[21,22,31]。通过坐标转换，将该积分转换到球面-径向坐标系中：

(15)

其中，Un={y∈n|yTy=1}为超球面。

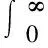
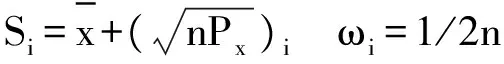
(16)

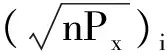
从式可知，3阶CKF具有完全对称的样本点，以及相同的非负权重。这使得3阶CKF比UKF具有更好的稳定性。在高维和高非线性的系统中，3阶CKF的滤波精度可能无法满足要求。Jia等人[22]给出了5阶CKF，并在仿真中对5阶CKF进行了分析和讨论。

2 增广容积卡尔曼滤波算法

2.1 增广球面-径向容积法则

本小节将给出增广容积卡尔曼滤波(ACKF)算法的具体形式。在此之前，为了不失一般性与方便讨论，考虑如下一步非线性变换函数：

u=g(x)+e

(17)

其中，x∈n，均值与协方差分别为和Px；e∈m，均值与协方差分别为0和E。

将式改写为增广形式：

u=ga(xa)=g(x)+e

(18)

其中，xa=[xT,eT]T，均值和协方差分别为：

(19)

(20)

以3阶球面径向容积法则为例，增广形式的样本及其权重如下所示：

(21)

其中，i=1,2,…,na，na=n+m。

将式(19)、式(20)代入式(21)，得到：

(22)

其中，j=1,2,…,n，l=1,2,…,m；以上所有样本点都具有相同的权重1/2na。

2.2 增广容积卡尔曼滤波算法

为了将增广卡尔曼滤波算法适用于动态系统式(1)、式(2)中，先将其写成增广形式：

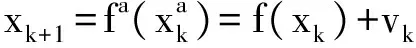
(23)

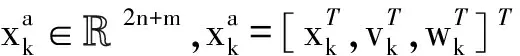
(24)

(25)

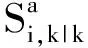
(26)

(27)

在增广形式下，式(7)中不再包括过程噪声项Qk。

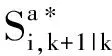
3 目标跟踪仿真

在本节中，将考虑一个空中交通管制系统[21]。在该系统中，空中飞行器按照指定角速度在水平面上做转弯动作。飞行器在空中水平面的轨迹如图1所示[21]。

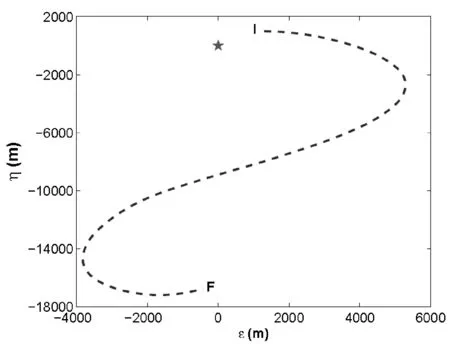
图1 飞行器轨迹(I-起点，F-终点，★-雷达站)

该转弯动作可以通过如下动态系统模型表征[21]：

xk-1+vk-1

(28)

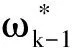
其中：

在测量站，雷达只能测量目标飞行器与自身的相对距离和夹角。因此，测量方程为：

(29)

其中，nk是均值和协方差分别为0和Rk=diag[1 000,100]的高斯白噪声。

本次仿真实验中，系统状态的初始真实值为：

x0=[1 000m,300ms-1,1 000m,0ms-1,-3°s-1]T

P0=diag[1 000m2,10m2/s2,100m2,10m2/s2,100mrad2/s2]

在k=0，系统状态的均值和协方差最优估计分别为x0|0=x0和P0|0=P0。仿真时间长度为200s，采样间隔Δt=1。

为了对CKF和ACKF的滤波性能进行评价，引入评价标准根均方误差(RMSE)。本仿真中，位置信息的RMSE的定义如下[22]：

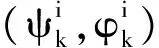
在目标跟踪测试中，系统状态的RMSEs时间平均值统计结果如表1所示。3阶ACKF、3阶CKF、5阶CKF以及UKF(κ=3-m=-2)的计算复杂度或计算时间开销如表2所示。系统状态的仿真结果如图2-图4所示。

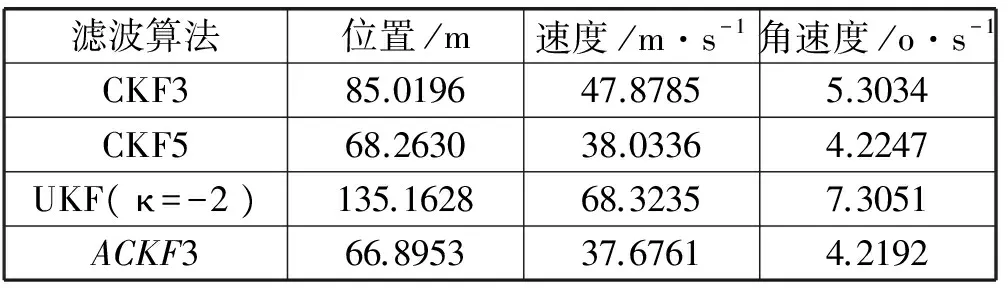
表1 各算法的RMSEs

表2 各算法的样本数与计算时间

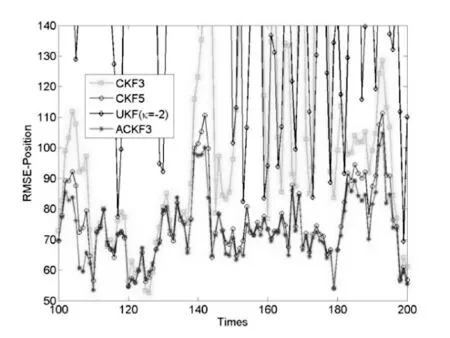
图2 位置RMSE

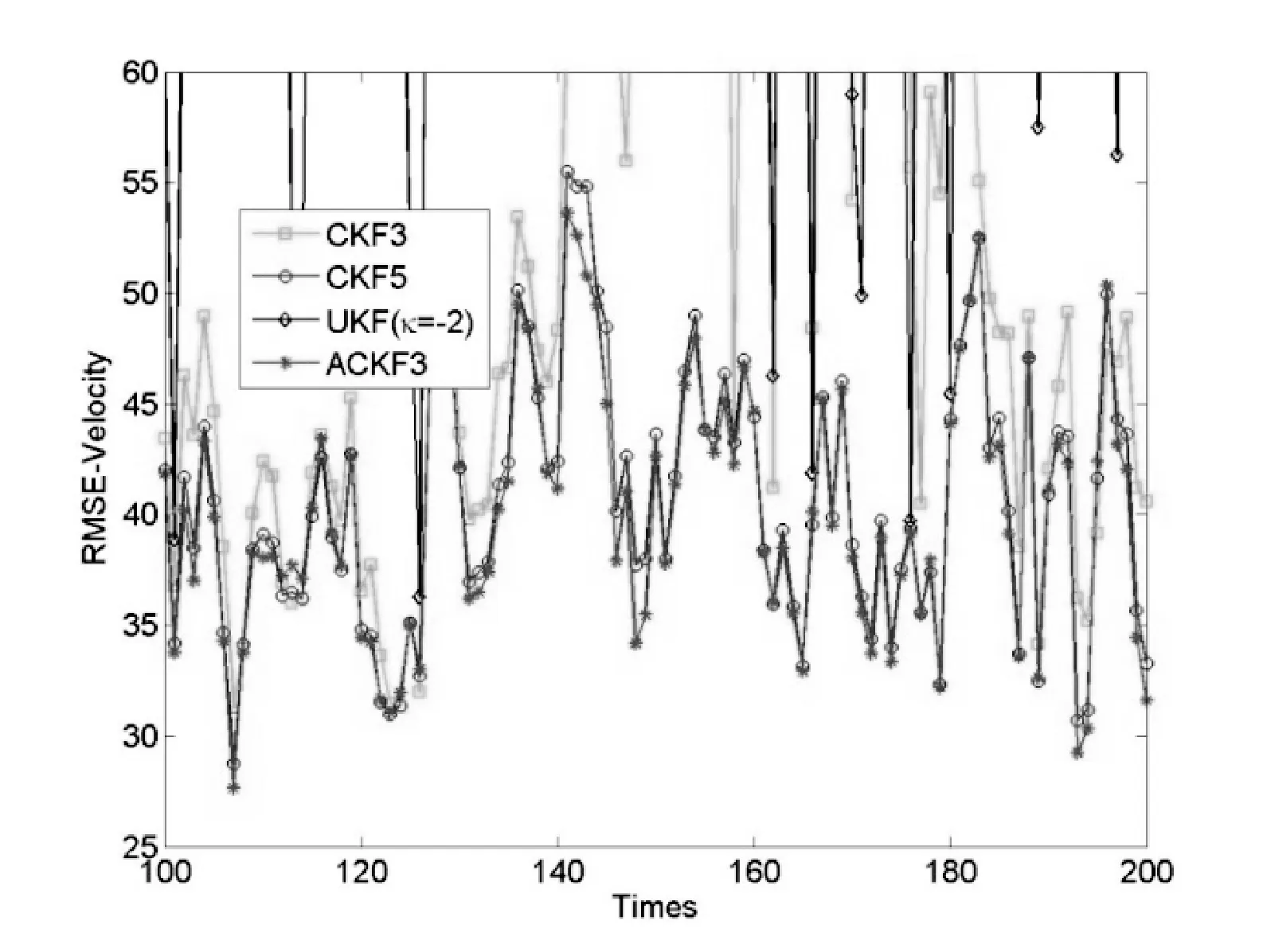
图3 速度RMSE

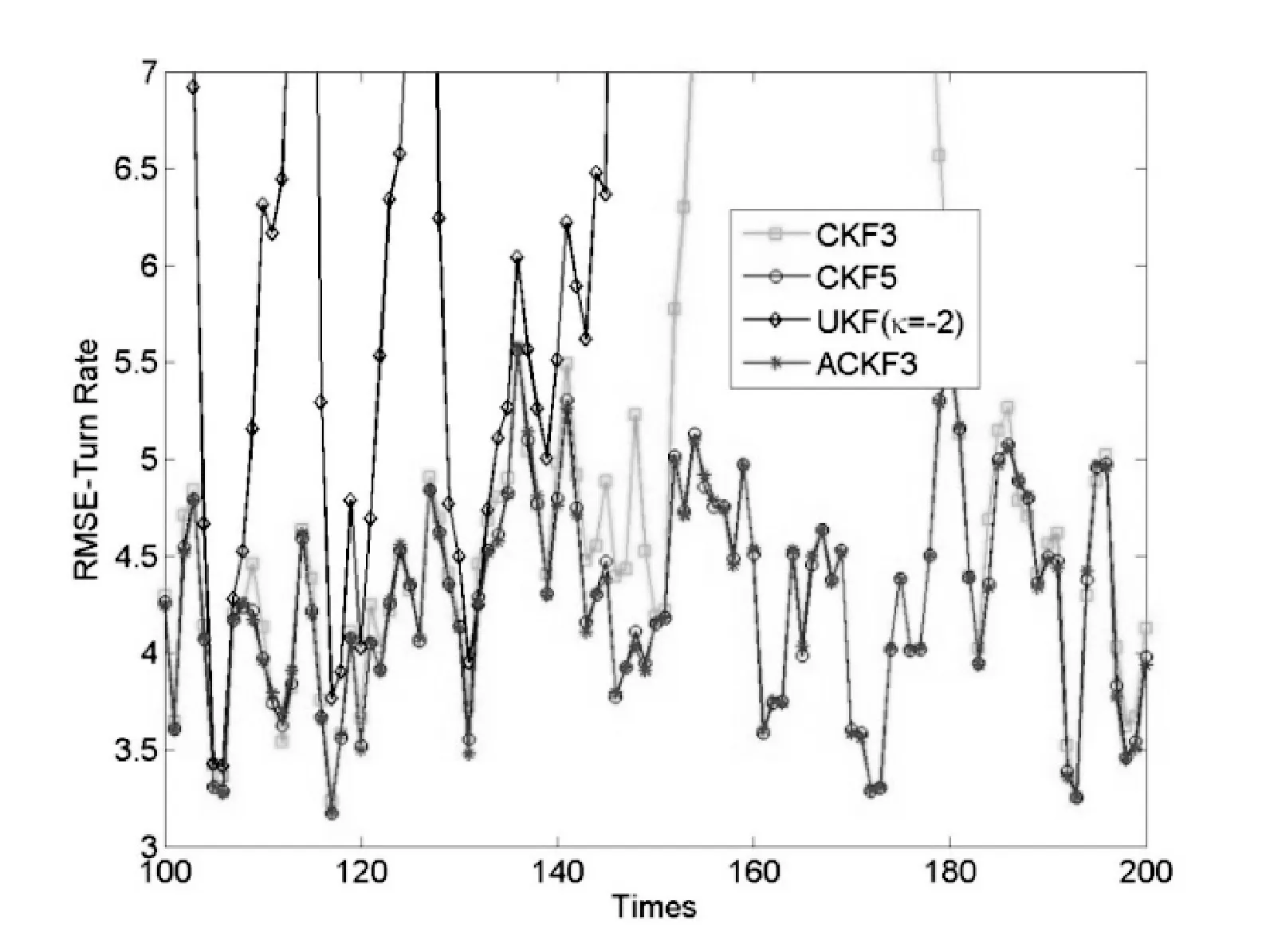
图4 角速度RMSE

从图2-图4可知，3阶ACKF在位置、速度和角度上的RMSE明显优于3阶CKF和UKF(κ=-2)，尤其是在位置和速度分量。这可能是由位置和速度分量的高非线性度，以及低测量精度导致。相比于5阶CKF，3阶ACKF依然具有更好的滤波精度。同时，3阶CKF3和UKF(κ=-2)的RMSE曲线波动幅度明显大于3阶ACKF。这表明3阶ACKF的滤波性能比3阶CKF更加稳定。同时，κ=-2使得UKF中出现负权重，这可能导致UKF的出现协方差非正定性以及目标跟踪失败问题。根据表1可知，3阶ACKF的统计RMSEs明显好于3阶CKF和UKF(κ=-2)；略为好于5阶CKF。表2显示，3阶ACKF的计算时间高于3阶CKF和UKF，且近似地正比于样本数。与5阶CKF相比，3阶ACKF的样本数只有其近似一半，却获得更好的滤波性能。从数值积分的角度分析，3阶ACKF比3阶CKF采用更多的样本数，更好地逼近非线性系统的分布；利用系统噪声和测量噪声，更好地匹配状态的奇数阶矩信息，获得更好的滤波精度和稳定性；而且其正权重保证了滤波的稳定。

4 结 语

本文对UKF、AUKF、和CKF在非线性目标跟踪系统中的性能做了分析比较，并给出了ACKF以及3阶ACKF的样本点和权重。在5维的高非线性目标跟踪模型中，3阶ACKF比3阶CKF、5阶CKF和UKF(κ=-2)具有更好的滤波精度和稳定性，以及可接受的计算复杂度。因此，对于高维非线性目标跟踪系统，ACKF是一个更好的选择。

[1] 孔军,汤心溢,蒋敏,等.基于多尺度特征提取的Kalman滤波跟踪[J].红外与毫米波学报,2011(5):446-450.

[2]GroverR,HwangP.IntroductiontorandomsignalsandappliedKalmanfiltering[J].InternationalJournalofAdaptiveControl&SignalProcessing,1992,6(5):516-518.

[3]UhlmannJK.Algorithmsformultiple-targettracking[J].AmericanScientist,1992,80(2):128-141.

[4]FrühwirthR.ApplicationofKalmanfilteringtotrackandvertexfitting[J].NuclearInstrumentsandMethodsinPhysicsResearchSectionA:Accelerators,Spectrometers,DetectorsandAssociatedEquipment,1987,262(2):444-450.

[5]EinickeGA,WhiteLB.RobustextendedKalmanfiltering[J].IEEETransactionsonSignalProcessing,1999,47(9):2596-2599.

[6]YangJ,SchonfeldD,MohamedM.Robustvideostabilizationbasedonparticlefiltertrackingofprojectedcameramotion[J].CircuitsandSystemsforVideoTechnology,IEEETransactionson,2009,19(7):945-954.

[7]ChangC,AnsariR,KhokharA.Multipleobjecttrackingwithkernelparticlefilter[C]//2005IEEEComputerSocietyConferenceonComputerVisionandPatternRecognition,Vol1,Proceedings,2005:566-573.

[8]OkumaK,TaleghaniA,DeFreitasN,etal.Aboostedparticlefilter:Multitargetdetectionandtracking[C]//ComputerVision-ECCV2004.City:Springer,2004:28-39.

[9]DoucetA,JohansenAM.Atutorialonparticlefilteringandsmoothing:Fifteenyearslater[J].HandbookofNonlinearFiltering,2009,12:656-704.

[10]JulierSJ,UhlmannJK.Ageneralmethodforapproximatingnonlineartransformationsofprobabilitydistributions[R].Technicalreport,RoboticsResearchGroup,DepartmentofEngineeringScience,UniversityofOxford,1996.

[11]ZhaoM,YuXL,CuiML,etal.SquareRootUnscentedKalmanFilterBasedonStrongTracking[C]//TheProceedingsoftheThirdInternationalConferenceonCommunications,SignalProcessing,andSystems,Springer,2015:797-804.

[12]JulierSJ,UhlmannJK.Unscentedfilteringandnonlinearestimation[J].ProceedingsoftheIEEE,2004,92(3):401-422.

[13] 张勇刚,黄玉龙,武哲民,等.一种高阶无迹卡尔曼滤波方法[J].自动化学报,2014,40(5):838-848.

[14] 黄铫,张天骐,高清山,等.一种提高无迹卡尔曼滤波精确度的方法[J].计算机仿真,2010,27(3):348-352.

[15]WangY,LiuJ,YangW,etal.AheuristicforSigmasetselectionofUKF[C]//SignalProcessing(ICSP),2014 12thInternationalConferenceon,2015:72-77.

[16]LiuJ,WangY,ZhangJ.AlinearextensionofUKFtohigher-ordermoment-matching[C]//DecisionandControl(CDC),2014IEEE53rdAnnualConferenceon,2014:5021-5026.

[17]WuY,HuD,WuM,etal.UnscentedKalmanfilteringforadditivenoisecase:augmentedvs.non-augmented[C]//ProceedingsoftheAmericanControlConference,2015:4051-4055.

[18]JulierSJ,UhlmannJK.AnewextensionoftheKalmanfiltertononlinearsystems[C]//ProceedingsofSpie,1997:182-193.

[19] 胡高歌,高社生,种永民,等.StochasticstabilityofthederivativeunscentedKalmanfilter[J].中国物理B(英文版),2015(7):64-73.

[20]HuberMF,HanebeckUD.Gaussianfilterbasedondeterministicsamplingforhighqualitynonlinearestimation[C]//Proceedingsofthe17thIFACWorldCongress,2008:13527-13532.

[21]ArasaratnamI,HaykinS.CubatureKalmanfilters[J].AutomaticControl,IEEETransactionson,2009,54(6):1254-1269.

[22]JiaB,XinM,ChengY.High-degreecubatureKalmanfilter[J].Automatica,2013,49(2):510-518.

[23]ZhaoY.PerformanceevaluationofcubatureKalmanfilterinaGPS/IMUtightly-couplednavigationsystem[J].SignalProcessing,2016,119:67-79.

[24] 鹿传国,冯新喜,张迪.基于改进容积卡尔曼滤波的纯方位目标跟踪[J].系统工程与电子技术,2012,34(1):28-33.

[25]PakkiK,ChandraB,GuDW,etal.Cubatureinformationfilteranditsapplications[C]//2011AmericanControlConference(ACC),IEEE,2011:3609-3614.

[26]PesonenH,PicheéR.Cubature-basedKalmanfiltersforpositioning[C]//PositioningNavigationandCommunication(WPNC),2010 7thWorkshopon,IEEE,2010:45-49.

[27]SinghAK,BhaumikS.Higherdegreecubaturequadraturekalmanfilter[J].InternationalJournalofControl,AutomationandSystems,2015,13(5):1097-1105.

[28] 潘泉,杨峰,叶亮,等.一类非线性滤波器—UKF综述[J].控制与决策,2005,20(5):481-489.

[29] 王小旭,潘泉,黄鹤,等.非线性系统确定采样型滤波算法综述[J].控制与决策,2012,27(6):801-812.

[30]LiP,YuJ,WanM,etal.TheaugmentedformofcubatureKalmanfilterandquadratureKalmanfilterforadditivenoise[C]//Information,ComputingandTelecommunication,2009.YC-ICT’09.IEEEYouthConferenceon,2009:295-298.

[31] 穆静,蔡远利.迭代容积卡尔曼滤波算法及其应用[J].系统工程与电子技术,2011,33(7):1454-1457.

AUGMENTED CUBATURE KALMAN FILTER FOR ADDITIVE NOISEAND ITS APPLICATION TO OBJECT TRACKING

Liu Jiang Ye Songqing

(ChongqingInstituteofGreenandIntelligentTechnology,ChineseAcademyofSciences,Chongqing400714,China)

Since the cubature Kalman filter (CKF) provides a good accuracy with low computational complexity, it is wildly applied in estimation and tracking systems. But for a tracking system involving high dimensionality and acute nonlinearity, 3-degree CKF and high-degree CKF encounter low accuracy and instability problems, respectively. To improve the the performance, augmented cubature Kalman filter for additive noise is discussed. In the simulation, CKF, UKF and ACKF are applied to 5-dimensional targets tracking system. Besides, their performances including accuracy, stability and complexity are compared by RMSEs. The results show that 3-degree ACKF can obtain better tracking accuracy and stability with acceptable computational complexity than UKF, 3-degree CKF and 5-degree CKF in highly nonlinear and dimensional systems.

Tracking Augmented CKF Nonlinear filter Additive noise

2016-01-18。国家自然科学

61202131)；中国科学院“西部之光”项目以及青年创新促进会项目(2015315)。刘江，副研究员，主研领域：计算机软件与理论，可计算理论。叶松庆，硕士生。

TP3

A

10.3969/j.issn.1000-386x.2017.03.025