一元二次方程的四种基本解法

江西省赣州市信丰县九渡中学(341600) 赖承勇 ●

一元二次方程的四种基本解法

江西省赣州市信丰县九渡中学(341600) 赖承勇 ●

一元二次方程和一元一次方程都是整式方程，它们是中学数学中的一个不可忽视的内容，它们不仅和二次函数有着密不可分的关系，也是初高中解决不等式问题的必须运用的知识之一．

一元二次方程所具备的三个特点:(1)只含有一个未知数;(2)未知数的最高次幂是2;(3)是整式方程．

一、直接开方法

例题1 解方程(3x+2)(3x－2)=4．

解析 因为(3x+2)(3x－2)=4，所以9x2－4=4，即，所以

评注 解一元二次方程时，通常先把方程化为一般式，而用直接开放法求解时，应注意方程两边同时开方时，只需要一边取正负号．如果形如(x+a)2=b时，应注意当b≥0时有解，否则无解．

二、配方法

例题2 解方程2x2－7x+2=0．

评注 在解决形如ax2+px+q=0的方程时，在使用配方法时，如果二次项系数不为1时，通常先把系数化为1，再进行配方．

三、公式法

例题3 某数学兴趣小组对关于x的方程(m+1) xm2+2+(m－2)x－1=0提出了一个问题:若使方程为一元二次方程，m是否存在?若存在，求出m并解此方程．

解析 存在．若使方程为一元二次方程，则m+1≠0，且m2+2=2，得m=0．

当m=0时，方程变为x2－2x－1=0．．因此，该方程是一元二次方程时，m=1，两根为

评注 在利用公式法求解一元二次方程的解时，需要先把方程化成一般形式进行求解，若b2－4ac≥0时，方程有解，否则方程无实数解．

四、因式分解法

例题4 解方程6x2－x－2=0．

解析 将方程左边用十字相乘法分解因式，有(2x+ 1)(3x－2)=0，所以2x+1=0或3x－2=0，从而x1=－

评注 在利用因式分解法时，方程一边必须为0，另一边可用任何方法分解因式．

变式训练1 (2015年湖北武汉四月调考)解下列方程:

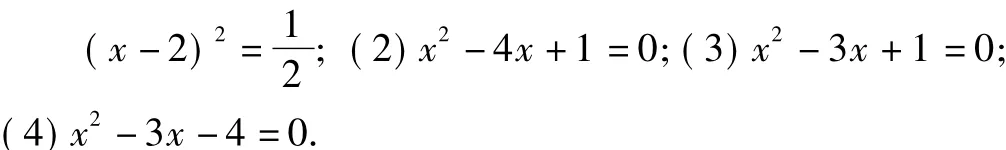
(3)因为 a=1，b=－3，c=1，所以 Δ=b2－4ac= (－3)2－4×1×1=5＞0，所以

(2)利用配方法得:(x－2)2=3，直接开平方，得x－2

(4)分解因式，得(x－4)(x+1)=0，即x1=4，x2=－1．

变式训练2 (2015年安徽省阜阳市第十五中学二模)请阅读下列材料:

问题:已知方程x2+x－1=0，求一个一元二次方程，使它的根分别是已知方程根的2倍．

请用阅读材料提供的“换根法”解答下列问题(要求:把所求方程化为一般形式):

(1)已知方程x2+x－2=0，求一个一元二次方程，使它的根分别为已知方程根的相反数，则所求方程为___;

(2)已知关于x的一元二次方程ax2+bx+c=0有两个不等于0的实数根，求一个一元二次方程，使它的根分别是已知方程根的倒数．

解析 (1)设所求方程的根为y，则y=－x，即x=－y．把x=－y代入已知方程，得y2－y－2=0．

变式训练3 (2015年湖南长沙中考真题)现代互联网技术的广泛应用，催生了快递行业的高速发展，据调查，长沙市某家小型“大学生自主创业”的快递公司，今年3月份与5月份完成投递的快递总件数分别为10万件和12．1万件，现假定该公司每月投递的快递总件数的增长率相同．

(1)求该快递公司投递总件数的月平均增长率;

(2)如果平均每人每月最多可投递0．6万件，那么该公司现有的21名快递投递业务员能否完成今年6月份的快递投递任务?如果不能，请问至少需要增加几名业务员?

解析 (1)设该快递公司投递总件数的月平均增长率为x，根据题意，得10(1+x)2=12．1，解得x1=0．1，x2=－2．2(不合题意，舍去)．答:该快递公司投递总件数的月平均增长率为10%．

(2)今年6月份的快递投递任务是12．1×(1+10%) =13．31(万件)．因为平均每人每月最多可投递0．6万件，所以21名快递投递业务员能完成的快递投递任务是0．6×21=12．6万件＜13．31万件，所以该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务，所以需要增加业务员(13．31－12．6)÷0．6≈2(名)．答:该公司现有的21名快递投递业务员不能完成今年6月份的快递投递任务，至少需要增加2名业务员．

选择恰当的方法能提高解题速度．(1)形如(x－a)2=b(a≠0)的方程可以用直接开平方法求解．(2)对于b为偶数又不易因式分解的可以用配方法较快解出．(3)对于b为奇数又不易因式分解的一元二次方程可以利用公式法求解．(4)能因式分解的就用因式分解法求解．

在解决一元二次方程的求解时，需要注意基本技能和解题技巧，方能胜券在握，当把基本方法掌握后，再对基本方法加以灵活运用，便可以做到熟能生巧．基础知识掌握扎实的情况下对以后学习将会起到事半功倍的作用．

G632

B

1008－0333(2017)02－0029－02