一道几何题的多种解法

湖南省郴州市北湖区郴州市九中(423000) 李林强 ●

一道几何题的多种解法

湖南省郴州市北湖区郴州市九中(423000) 李林强 ●

一、原题呈现

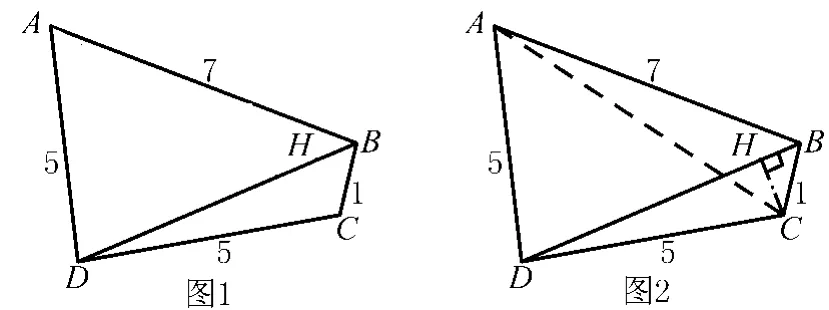
如图1、四边形ABCD中，∠ABC=∠CDA=90°，AD= DC=5，AB=7，BC=1，则BD=___．

二、解法展示

解法1 如图2，连接AC，过C点作CH⊥BD，垂足于H点．因为∠ABC=∠CDA=90°，所以，A、B、C、D四点共圆;又因为AD=DC=5，所以∠CAD=∠DCA=45°，所以△ACD是等腰直角三角形，所以∠CBD=∠CAD=45°．又因为BC=1，所以．在Rt△CDH中，CD=5，所△BCH是等腰直角三角形．所以由勾股定理可得:

解法2 如图3，把△DBC绕D点按逆时针方向旋转90°，得△DC'A．因为AD=CD=5，∠ADC=∠ABC=90°，所以∠ADC+∠ABC=90°，所以∠BCD+∠BAD=180°，由旋转对称性可知:∠BCD=∠DAC'，BD=DC'．BC=AC' =1，所以∠BAD+∠DAC=180°，所以B、A、C'三点在同一直线上，所以BC'=8，△BDC'是等腰直角三角形，BD=

解法3 如图4，分别延长AB、DC，两延长线交于E点．设BE=a，CE=b，过B点作BH⊥DE，垂足于H点．因为∠ADC=∠ABC=90°，所以∠A+∠DCB=180°．又因为∠BCD+∠BCE=180°，所以∠A=∠BCE．又因为∠E=∠E，所以△EBC∽△EDA，所以，即，所以5a=5+b①．在Rt△ADE中，有AD=CD=5，AB=7，由勾股定理得:AD2+DE2=AE2，即(a+7)2=52+(5+b)2②．把①式代入②式解得(舍去)．所以b=由可得．在Dt△BCH中，在Dt△BDH中，BD=

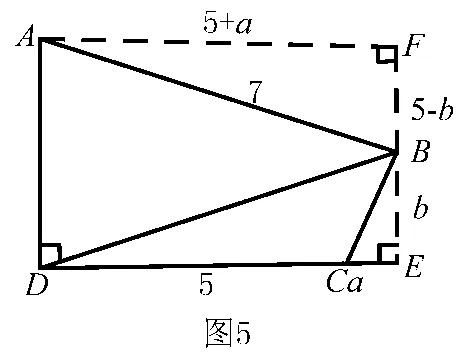
解法5 如图5，在四边形ABCD外部构造矩形ADEF．设CE=a，BE=b，那么BF=5－b，AF=5+a．由△AFB∽△BEC可得，即

在Rt△BDE中，

总之，这是一道好题，对培养学生的综合分析问题能力，所求问题转换图形的转换的思考很有益．一题多解的自然产生，基于扎实的数学思想、准确的切入点、教学问题的转换、一定的解决方法和解题技巧．建立教学模型，达到举一反三的效果．

复杂问题简单化，通俗易懂，符合学生的认知规律，有时图形转换能力要求较高，但解法的确来源于学生，对于不会做的通过讲解，很容易接受，因此也属于较自然的解法．

［1］文东．明晰本质，自然构造［J］．中学数学教学参考:中旬，2016(3):35－36

［2］王忠刚．一题多法的产生力求自然［J］．中学数学教学参考:中旬，2016(3):40－42

G632

B

1008－0333(2016)32－0025－01