基于Lamb波混合成像算法的薄板结构损伤定位

尹本进，李友荣，鲁光涛

(武汉科技大学机械自动化学院，湖北 武汉，430081)



基于Lamb波混合成像算法的薄板结构损伤定位

尹本进，李友荣，鲁光涛

(武汉科技大学机械自动化学院，湖北 武汉，430081)

针对传统椭圆法和双曲线法对结构损伤定位不精确的问题，提出了一种基于Lamb波的混合成像算法。该算法将椭圆法和双曲线法相结合，在使用相同数量传感器的条件下提高对信号数据的利用率，从而提高损伤定位的精度。通过有限元仿真对该算法进行验证，即建立一个无损伤模型和多个有损伤模型，模拟压电传感器以双面同相的激励方式获得单一模态的Lamb波，从而获得损伤的反射信号。用混合成像算法和传统椭圆法对仿真模型分别进行损伤定位。成像结果对比表明，混合成像算法对损伤的定位更精确，而且在结构有多处缺陷的情况下能检测到传统椭圆法无法识别出的损伤。

Lamb波；结构健康监测；损伤定位；椭圆法；双曲线法；成像算法；薄板结构

近年来，在航空航天、土木建筑等领域，由结构或设备损伤造成的事故屡见不鲜，往往导致财产损失和人员伤亡。在线健康监测能尽早发现隐藏的设备安全隐患，使结构检修和维护能及时进行，从而降低设备维修成本，提高结构使用寿命。

Lamb波具有传播距离远、能量衰减小、对结构损伤敏感等优点，被广泛用于结构健康监测中。Saravanos等[1]通过实验证明Lamb波可用于复合材料的结构损伤检测。赵军辉等[2]采用压电晶片双面同相和双面异相激励的方式来激发单一模态Lamb波，并对铝板中的裂纹进行了检测,结果表明S0模态Lamb波较A0模态Lamb波对裂纹识别能力要强一些。Lee等[3-4]利用Lamb波传输时间及幅值的衰减来表征结构损伤的程度并以此得到结构损伤位置信息。王强等[5]利用时间反转法对结构损伤反射波信号进行聚焦放大以提高信号的信噪比，并重构得到Lamb波波动图，最终得到了结构的损伤位置。Gorgin等[6]针对损伤形状提出一种基于概率的损伤识别方法，通过对接收到的Lamb波信号进行正态分布处理，并采用该分布的峰值所在的部分区间作为损伤部位。张宇[7]提出一种基于最大相似性原理与遗传算法相结合的方法对结构损伤反射波进行重构并获得结构损伤信息。郭杜斌等[8]提出了超声多途检测技术，通过仿真和实验证明超声多途可以对薄板缺陷进行定位识别，并得到损伤的尺寸大小。张帅芳[9]在ABAQUS有限元分析结果的基础上，利用四点定位法对结构损伤进行识别与定位。Kehlenbach等[10]采用椭圆法对结构损伤进行定位检测。Yu等[11]基于信号激励器、传感器和缺陷三者之间的几何位置关系提出一种双曲线定位方法并用于对结构缺陷进行定位。刘增华等[12]设计了一种集Lamb波A0单模态低频激励器及接收器于一体的压电陶瓷传感器，并采用椭圆成像和数据融合技术相结合的方法对结构损伤进行成像定位识别。Lu等[13]提出一种基于逻辑运算的时间延时叠加成像算法对铝板损伤进行了定位识别。

传统的基于Lamb波的椭圆或双曲线成像定位方法主要利用损伤反射波信号来绘制椭圆或双曲线，并通过不断叠加得到结构损伤的位置，其定位精度与传感器的数量成正比。然而，由于结构自身及监测成本的限制，往往只能在被监测结构表面粘贴有限数量的传感器。因此，如何有效利用有限的传感器来提高成像精度显得尤为重要。本文提出一种混合时间延时叠加成像算法,即将椭圆法和双曲线法相结合并通过延时叠加成像技术对铝板孔状损伤进行成像定位。与传统的时间延时叠加成像算法相比，本文算法在采用相同数量传感器的条件下可大大提高结构损伤的定位精度。

1 结构损伤成像定位基本理论

1.1 椭圆法

如图1所示，在Lamb波激励器S0处激发应力波，该应力波可从S0直接传播到信号接收传感器Si处，也可从S0经损伤处F反射后再到达Si。由此，结构损伤的反射信号ri(t)为

ri(t)=xi(t)-xbi(t)

(1)

式中：xi(t)为结构中存在损伤时传感器接收到的信号；xbi(t)为结构中无损伤时传感器接收到的信号；i为传感器编号。进一步，反射信号的传播时间ti为

(2)

式中：LS0-F-Si是Lamb波从激励器通过结构损伤反射传播到接收器所经过的距离；c0为Lamb波传播的群速度。Lamb波在各向同性介质中的传播速度c0由材料的物理特性及Lamb波的频率决定，与传感器的布置位置无关，因此可事先进行标定。当c0确定后，ti可通过传感器测得，则‖S0F‖+‖SiF‖为定值。由椭圆几何原理可知，损伤点F在以S0和Si为焦点的椭圆上。若Sj为另一传感器，则损伤点F也在以S0和Sj为焦点的椭圆上。两个椭圆的交点即为损伤点F所在位置。

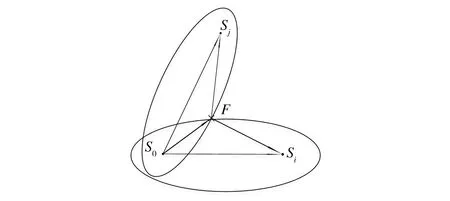
图1 椭圆法示意图

1.2 双曲线法

如图2所示，S0是信号激励器，Si、Sj、Sk是信号接收传感器。与椭圆法同理可得

(3)

(4)

式(3)与式(4)相减可得

(5)

由式(5)可知,损伤点F在以Sj和Si为焦点的双曲线上。两对双曲线的交点即为损伤所在位置[11]。

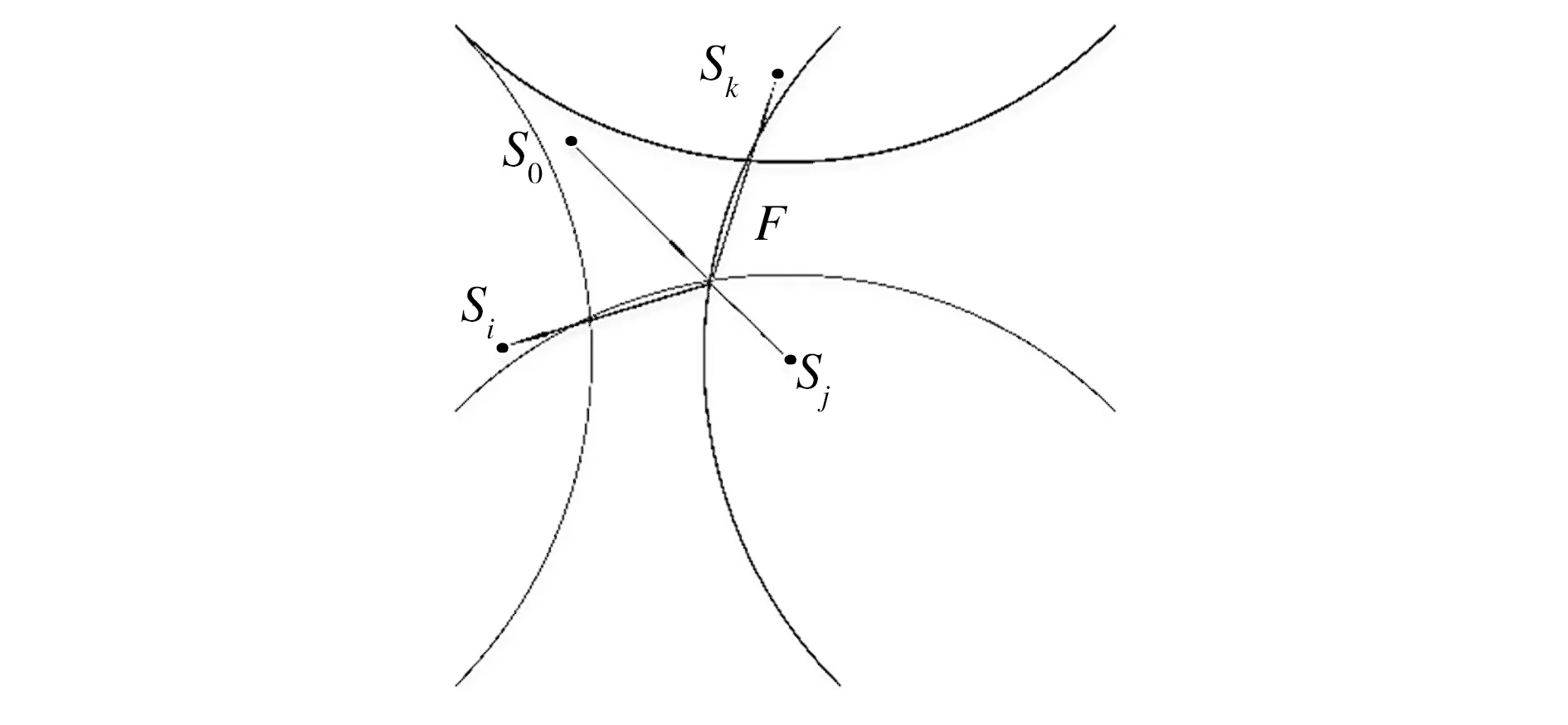
图2 双曲线法示意图

椭圆法和双曲线法都是基于传感器和损伤的几何位置关系而提出的，因此可以将椭圆法和双曲线法结合起来。在使用一个激励器和N个信号接收传感器的条件下，椭圆法能产生N个有效数据，双曲线法能产生N(N-1)/2个有效数据。两种算法结合后，在使用相同数量传感器的条件下，会有N(N+1)/2个有效数据，从而提高对数据的利用率。这样不仅能减少伪像，而且使真实损伤的定位更加精确。

2 损伤成像算法

2.1 反射系数的确定

传感器接收到的信号里面除了包含损伤反射信号以外，还存在边界反射信号。为了减小边界反射信号对成像结果的影响，定义了一个反射系数，据此对边界反射信号进行“滤波”处理。反射系数的计算公式为

(6)

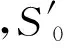
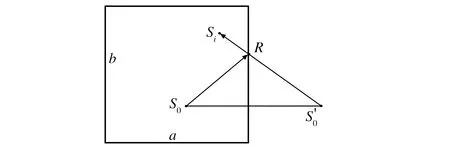
图3 边界反射示意图

加入反射系数后的信号可表示为

(7)

2.2 信号幅值的归一化

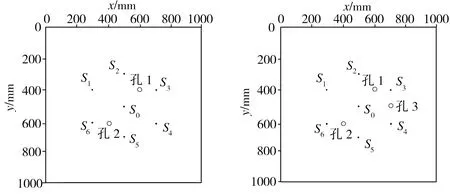
Lamb波在向周围传播过程中，振幅会随其传播距离产生衰减。为了使每个传感器接收到的信号对缺陷定位所产生的作用均相同，信号需要进行归一化处理。以第一个到达的脉冲波的波峰作为参考进行归一化处理,处理后的信号为

(8)

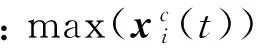
(9)

2.3 成像计算

根据椭圆法定位原理，对成像区域每个像素点进行赋值。由多个传感器得到像素点(x,y)的像素值为

(10)

其中,t(x,y)根据下式计算：

(11)

式中：S0(x)、S0(y)分别为信号激励器S0的x、y坐标；Si(x)、Si(y)分别为信号接收器Si的x、y坐标；toff为激励信号的最大波峰时刻与起始时刻的时差。同理，根据双曲线法原理，缺陷定位图像矩阵的计算表达式如下：

(12)

式中：rij(t)为ri(t)和rj(t)的互相关矩阵；Δt(x,y)由下式计算：

(13)

最终的图像像素矩阵为

I(x,y)=I1(x,y)·I2(x,y)

(14)

将像素矩阵I(x,y)缩放在0～1 dB的范围内，其中像素值为1 dB的位置代表缺陷位置。

3 有限元模拟

为了对本文所提出的算法进行验证，通过有限元方法模拟Lamb波在薄铝板中的传播过程，并利用本算法对铝板上孔状缺陷进行成像定位研究。铝板尺寸规格为1000 mm×1000 mm×1 mm，材料密度为2700 kg/m3，弹性模量为70 GPa，泊松比为0.33。

为了减小入射波入射角度及损伤反射波反射角度的影响，薄板结构的模拟损伤采用半径为5 mm的圆形通孔，且传感器呈圆周分布。一共建立了4个损伤模型，如图4所示,另外还设置1个无损伤模型进行对比分析。每个损伤模型中具体的通孔位置坐标见表1，所有模型中Lamb波激励器(S0)及接收传感器(S1～S6)的布置相同，其位置坐标见表2。

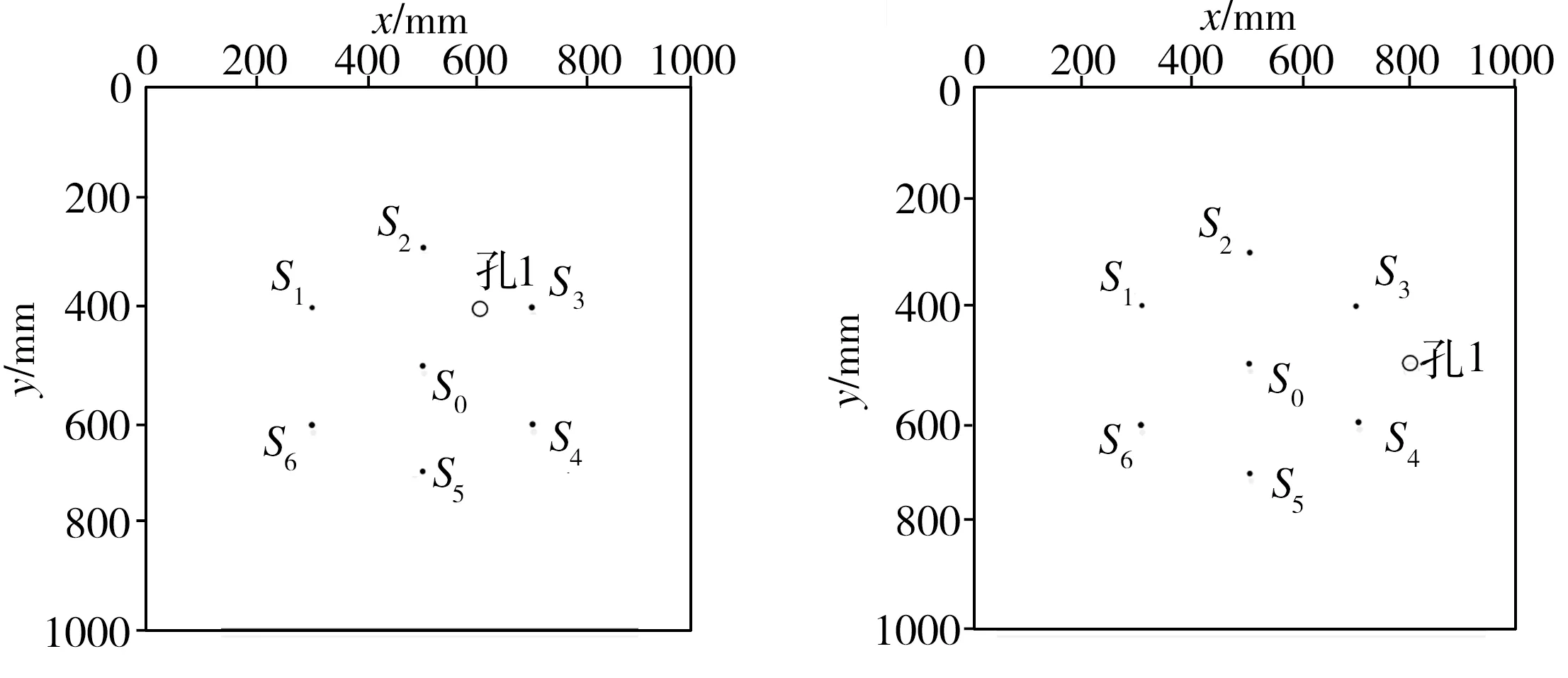
(a)损伤模型1 (b)损伤模型2

(c)损伤模型3 (d)损伤模型4

图4 损伤模型

Fig.4 Damage models

由于单一模态Lamb波对损伤较敏感[2]，且损伤反射波易于分析，故本文采用薄板双侧对称点同时激发的方式来施加载荷以产生单一S0模态的Lamb波。激励信号为高斯调制正弦脉冲信号，信号的中心频率为200 kHz，相对带宽为0.6，激励信号的时域波形如图5所示。

表1 损伤模型中孔的坐标(单位：mm)

表2 信号激励器和接收传感器的坐标(单位：mm)

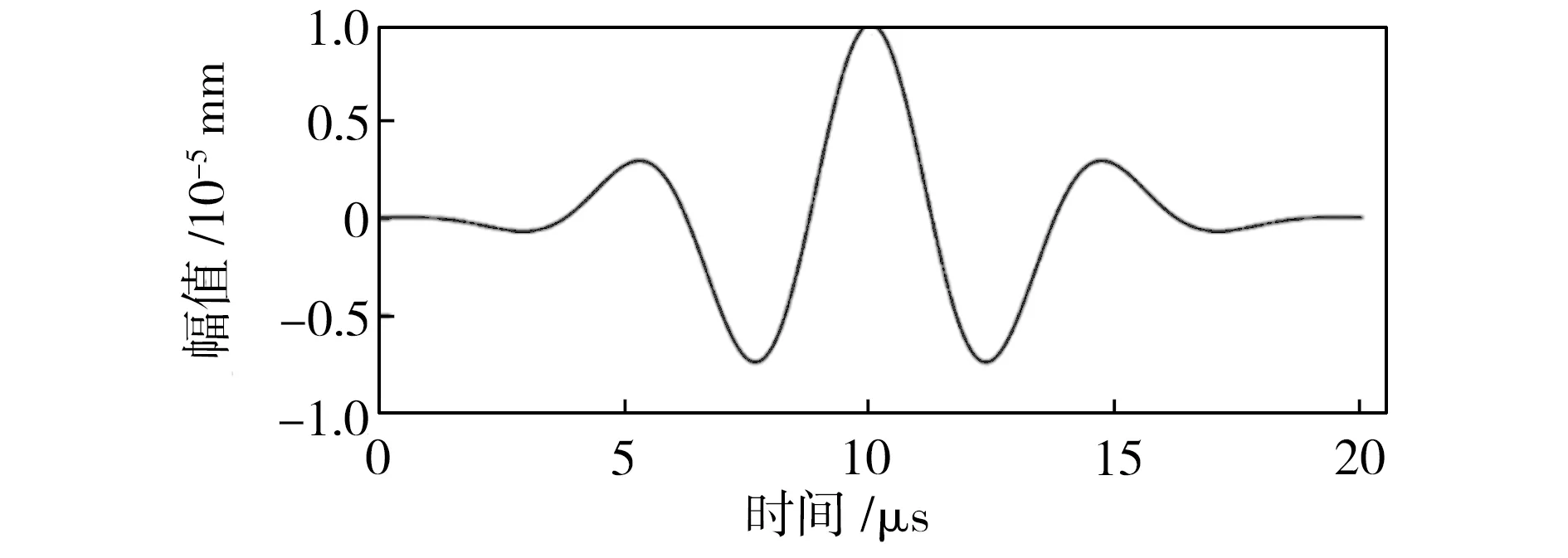
图5 激励信号波形图

4 损伤成像结果与分析

图6为传感器S6接收到的时域波形图,图中实线为损伤模型4的信号，虚线为无损伤模型信号。对比两个模型信号可以看出，第一个波是直接到达的首波，随后两个很小的波是通孔的反射波，另外一个通孔的反射波与边界反射波重叠。

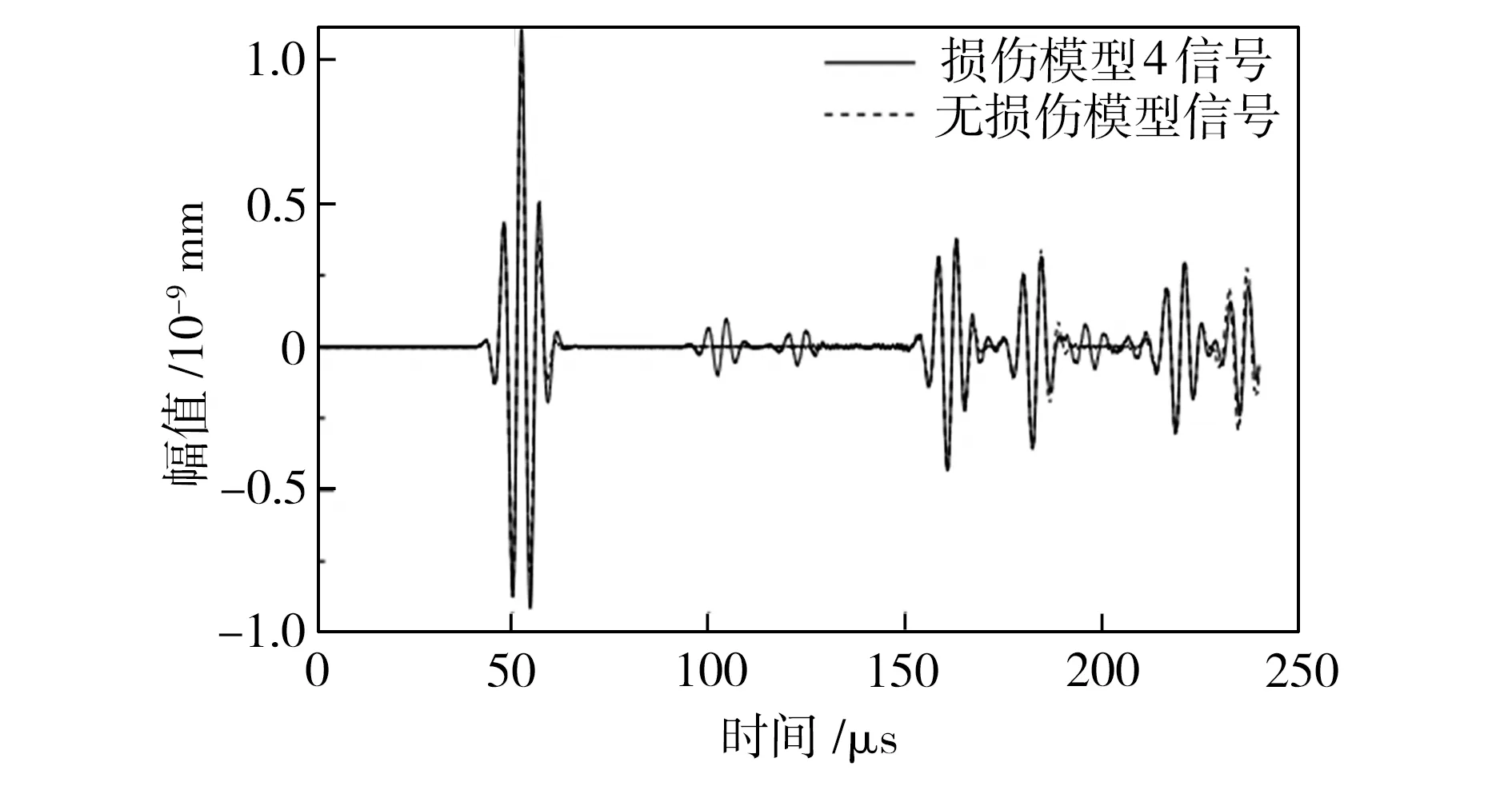
图6 传感器S6接受的时域信号

分别采用传统椭圆法[10]和本文提出的混合成像算法对4个模型进行损伤定位，其中模型4的损伤定位成像结果如图7和图8所示。将成像结果与损伤实际位置做误差分析，结果如表3所示。

(a)整体成像结果 (b)孔1局部放大

(c)孔2局部放大 (d)孔3局部放大

图7 损伤模型4采用传统椭圆法的成像结果

Fig.7 Imaging result of damage model 4 by traditional ellipse method

(a)整体成像结果 (b)孔1局部放大

(c)孔2局部放大 (d)孔3局部放大

图8 损伤模型4采用混合成像算法的成像结果

Fig.8 Imaging result of damage model 4 by hybrid algorithm

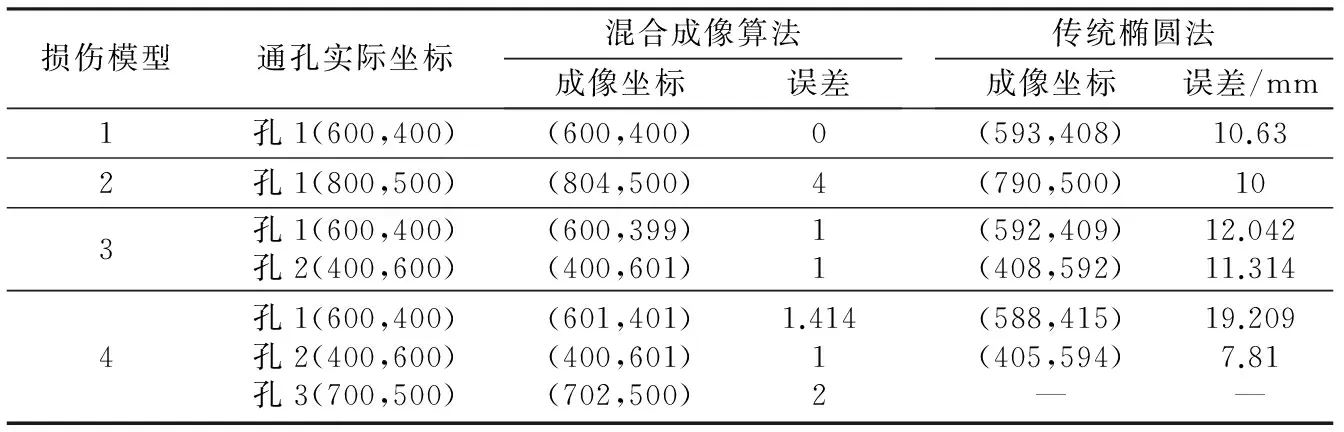
表3 成像结果及误差(单位：mm)

由图7、图8和表3中的成像结果对比可以看出，对于损伤模型4，传统椭圆法可检测出两处损伤，而本文提出的混合成像定位法可将3处损伤全部检测出来；对于全部4个模型，混合成像算法的定位精度均更高。由于缺陷是半径为5 mm的圆孔，而计算时选择以圆心坐标为基准，因此混合成像算法也会产生一些较小的定位误差，但相较椭圆法来说误差要小得多。

5 结语

针对薄板损伤检测问题，本文以椭圆法和双曲线法为基础提出混合成像算法，阐述了该算法的基本原理。利用有限元方法模拟压电传感器，同时采用双面同相的激励方式获得单一S0模态的Lamb波,很好地展现了Lamb波在薄板中的传播过程。利用混合成像算法和椭圆法分别对仿真模型进行损伤成像定位，成像结果对比分析显示，相较于传统的椭圆法，混合成像算法对损伤的定位更精确，其不仅在只有一个结构缺陷的情况下有很好的检测效果，而且在有多处结构缺陷的情况下依然适用。

[1] Saravanos D A, Heyliger P R. Coupled layerwise analysis of composite beams with embedded piezoelectric sensors and actuators[J]. Journal of Intelligent Material Systems and Structures, 1995,6(3): 350-363.

[2] 赵军辉,魏勤,袁媛，等.Lamb波检测板中裂纹的有限元模拟[J].压电与声光,2013,35(3):320-324,328.

[3] Lee B C, Staszewski W J. Lamb wave propagation modelling for damage detection(I): two-dimensional analysis[J]. Smart Materials and Structures, 2007,16(2): 249-259.

[4] Lee B C, Staszewski W J. Lamb wave propagation modelling for damage detection(II): damage monitoring strategy[J]. Smart Materials and Structures, 2007,16(2): 260-274.

[5] 王强，袁慎芳.主动Lamb波结构健康监测中信号增强与损伤成像方法[J].航空学报,2008,29(4):1061-1067.

[6] Gorgin R, Wu Z J, Gao D Y, et al. Damage size characterization algorithm for active structural health monitoring using the A0mode of Lamb waves[J]. Smart Materials and Structures, 2014,23(3): 035015.

[7] 张宇.基于Lamb波的结构损伤检测技术方法研究[D].西安：西北工业大学，2014.

[8] 郭杜斌，沈希忠，王磊.金属薄板缺陷的超声多途Lamb波检测[J].计算机测量与控制,2016,24(1):20-27.

[9] 张帅芳.超声导波在板中传播的时域频域数值模拟[D].大连：大连理工大学，2014.

[10]Kehlenbach M, Hanselka H. Automated structuralintegrity monitoring based on broadband Lamb wave excitation and matched filtering[C]//44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Norfolk, Virginia, 7-10 April, 2003: 1486-1492.

[11]Yu L, Cheng L, Su Z Q. Correlative sensor array and its applications to identification of damage in plate-like structures[J].Structural Control and Health Monitoring, 2012, 19(8): 650-671.

[12]刘增华，穆云龙，宋国荣，等.复合材料板Chirp激励的Lamb波成像技术研究[J].仪器仪表学报,2015,36(9):1961-1971.

[13]Lu G T, Li Y Y, Song G B. A delay-and-Boolean-ADD imaging algorithm for damage detection with a small number of piezoceramic transducers[J]. Smart Materials and Structures, 2016, 25(9): 095030.

[责任编辑 尚 晶]

Damage location for thin plate structures using hybrid imaging algorithm based on Lamb waves

YinBenjin,LiYourong,LuGuangtao

(College of Machinery and Automation, Wuhan University of Science and Technology, Wuhan 430081, China)

Aiming at the inaccuracy of structural damage location using traditional ellipse and hyperbola methods, a hybrid imaging algorithm based on Lamb waves is proposed. It combines ellipse method with hyperbola method to improve the utilization efficiency of signal data from the same number of sensors and the accuracy of damage location.The algorithm is verified by finite element simulation. A damage-free model and several damage models are established to simulate that piezoelectric sensors receive a single mode Lamb wave by the double-sided in-phase incentive method,and then reflection signals of the damages are obtained.The hybrid imaging algorithm and traditional ellipse method are used to detect damages in the models.The comparison of imaging results shows that the proposed hybrid imaging algorithm is more accurate in damage location and can identify multiple defects in the same structure which are beyond the identification ability of ellipse method.

Lamb waves; structural health monitoring; damage location; ellipse method; hyperbola method; imaging algorithm; thin plate structure

10.3969/j.issn.1674-3644.2017.02.010

2016-12-20

国家自然科学基金资助项目(51278084).

尹本进(1992-)，男，武汉科技大学硕士生.E-mail:yinben1992@163.com

李友荣(1946-)，男，武汉科技大学教授，博士生导师.E-mail:liyourong@wust.edu.cn

TH878；TB302

A

1674-3644(2017)02-0132-06