基于模态叠加法的面压载荷与基础激励等效方法

张 鹏 费庆国 吴邵庆 李彦斌

(东南大学土木工程学院, 南京 210096)

基于模态叠加法的面压载荷与基础激励等效方法

张 鹏 费庆国 吴邵庆 李彦斌

(东南大学土木工程学院, 南京 210096)

基于模态叠加法,将随机面压载荷等效为随机基础激励,为薄壁构件的振动台试验替代成本较高的噪声试验提供依据．该方法要求等效前后2种载荷作用下主模态位移一致,将单源载荷等效这一超静定问题合理简化为静定问题．以炭/炭复合材料悬臂板为研究对象,来验证载荷等效方法的有效性．分析结果显示,在随机面压载荷及等效随机基础激励作用下,板上典型部位随机正应力响应的功率谱密度高度吻合,在分析频段内危险点处x轴向正应力响应均方根分析误差低于1%,分布在板上的5个响应点处x轴向正应力响应均方根分析误差低于2%．该方法能有效地将随机面压载荷等效为基础激励,保证等效前后2种载荷作用下薄壁构件的随机动应力响应在频域及空间域上的分布一致性．

面压载荷; 基础激励; 载荷等效; 替代试验; 模态叠加法

高强随机脉动压力作用下先进复合材料结构的力学行为是工程上较为关注的问题之一[1-3]．在高强随机脉动压力作用下,复合材料薄壁结构可能会发生疲劳破坏[4]．在设计阶段,必须通过地面试验分析校核结构的可靠性．然而,噪声试验对设备的要求较高．在构件级设计阶段,复合材料的性能具有较大离散性,需开展批量试验分析,从而导致噪声试验的实施成本较高．因此,寻求一种节约成本的替代试验分析方法具有现实意义．振动台基础激励对平板类构件的作用效果类似于面压载荷,等同于一种分布载荷．振动台可以同时对多个较小尺寸构件施加基础激励,振动台试验的实施成本较低,因而采用振动台基础激励试验代替噪声试验具有较高的可行性．开展替代试验的关键是进行载荷等效,即将随机面压载荷等效为振动台基础激励的强迫位移载荷．

载荷等效在工程中得到了广泛的应用,主要包括将动载荷等效为静载荷[5-10]以及将动载荷等效为动载荷[11]两种情况．将动载荷等效为静载荷可有效简化结构在动载荷作用下的响应分析过程,提高结构强度、刚度设计以及结构优化设计的效率．该类方法主要包括加速度等效静载荷法[5]、位移等效静载荷法[6-7]、应力等效静载荷法[8-9]和能量等效静载荷法[10],其等效原则为,在等效前后2种载荷作用下,结构特定响应量相等．将动载荷等效为动载荷一般服务于疲劳寿命评估,其目的主要是简化疲劳试验加载、加速疲劳试验过程,等效原则为,等效前后结构关键部位的损伤量相同或呈特定比例[11]．

本文以C/C复合材料悬臂板为研究对象,基于模态叠加法,将板面受到的随机面压载荷等效为基础激励的随机强迫位移载荷．该载荷等效方法将动载荷等效为动载荷．将动应力响应作为疲劳寿命评估的输入条件.为服务于疲劳寿命评估,要求在随机面压载荷和等效基础激励的随机强迫位移载荷这2种载荷作用下,复合材料板上的随机动应力响应一致．特定频率点处结构的最大动应力响应多由单个主模态主导,因此上述载荷等效的直接目标为,载荷等效前后分析频率点处主模态的随机位移响应一致．分析结果表明,以主模态位移为直接等效目标,可使等效前后2种载荷作用下,结构上的随机动应力响应在频域及空间域上分布一致．

1 基础理论

1.1 模态叠加法

对于一个具有N自由度的线性平板结构,在板一侧的面压载荷p(ω)作用下(见图1(a)),频域内的动力学方程为

(-ω2M+jωC+K)X(ω)=Lp(ω)

(1)

式中,M,C,K分别为N×N阶质量矩阵、阻尼矩阵和刚度矩阵;X(ω)为结构在频域内的N×1阶位移响应向量,其中ω为角频率;L为N×1阶面压载荷影响向量,取决于面压载荷的有限元离散．式(1)由时域变换而来,该变换的初始条件为,初始位移与初始速度均为零．

(a) 面压载荷 (b) 基础激励

模态坐标系下频域内结构动力学方程为

(-ω2Mq+jωCq+Kq)Xq(ω)=ΦTLp(ω)

(2)

式中,Φ=[φ1φ2…φq]为N×q阶满足质量归一化条件的正则模态振型矩阵,其中,φi为第i阶模态振型,q为模态截断后的模态数;Mq,Cq,Kq分别为q×q阶模态质量矩阵、模态阻尼矩阵和模态刚度矩阵,且Mq=ΦTMΦ=I;Xq(ω)为结构在频域内的q×1阶模态位移响应向量,且X(ω)≈ΦXq(ω)．

求解方程(2),可得第i阶模态的位移响应xi(ω)为

xi(ω)=Hip(ω)p(ω)

(3)

式中,Hip(ω)为第i阶模态位移响应对面压载荷p(ω)的频响,即结构在单位面压载荷作用下第i阶模态的位移响应,且

(4)

式中,ωi为第i阶模态的固有频率．

进一步可求得随机面压作用下结构在任一自由度k上随机位移响应的自功率谱密度为

(5)

式中,Spp(ω)为随机面压载荷的自功率谱密度．

1.2 等效基础激励

令结构在固支或简支边界上的节点为约束节点,其余节点为非约束节点．当结构受到基础作用时,约束节点的位移等于基础激励的强迫位移载荷xe(ω) (见图1(b)),结构在频域内的动力学方程为

(-ω2M+jωC+K)X(ω)=0

(6)

式中,结构在频域内的位移响应X(ω)可表示为基础激励强迫位移xe(ω)与非约束节点相对约束节点的相对位移Xm(ω)之和,即

(7)

式中,Xm(ω)为m×1阶相对位移向量,其中,m+n=N,m为非约束自由度个数,n为约束自由度个数;E为N×1阶强迫位移载荷的影响向量,对应xe(ω)方向位移自由度的元素为1,其余为0．

令

(8)

将式(7)和(8)代入式(6)可得

(-ω2M+jωC+K)Y(ω)=Q(ω)xe(ω)

(9)

式中,Q(ω)为基础激励作用下等效节点力激励的N×1阶影响向量,且

Q(ω)=-(-ω2M+jωC+K)E

(10)

式(9)与式(1)具有相同的形式,等同于在分布载荷作用下的结构动力学方程．可通过模态叠加法求解式(9),得到第i阶模态的位移响应为

yi(ω)=Hie(ω)xe(ω)

(11)

式中,Hie(ω)为第i阶模态位移响应对基础强迫位移载荷xe(ω)的频响,即结构在单位基础强迫位移载荷作用下第i阶模态的位移响应,且

(12)

进一步可求得随机基础激励作用下结构在任一自由度k上随机相对位移响应的自功率谱密度为

(13)

式中,See(ω)为基础激励随机强迫位移的自功率谱密度．

按位移等效原则,当基础激励作用下任一自由度k上的相对位移响应与面压载荷作用下该自由度上的绝对位移响应一致时,2种载荷作用下结构上的应力分布也一致,此时可认为该基础激励为面压载荷的等效载荷,有

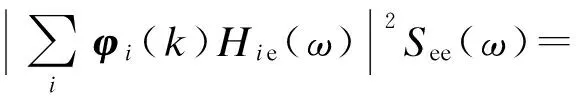
(14)

面压载荷及基础激励均为单源载荷,因此式(14)为超静定问题．结构低频响应一般由频率点处的主模态主导,忽略其余模态对响应的贡献,式(14)可简化为

(15)

式中,Hdp(ω)为第d阶模态位移响应对面压载荷p(ω) 的频响;Hde(ω)为第d阶模态位移响应对面压载荷xe(ω)的频响．

基于式(15),可求得等效基础激励的强迫位移功率谱为

(16)

根据式(16),将随机面压载荷等效为基础激励的随机强迫位移载荷,其等效原则为,等效前后主模态的位移响应一致．由式(16)获得的等效载荷可最大限度地满足式(14)所示的超静定方程．

2 算例验证

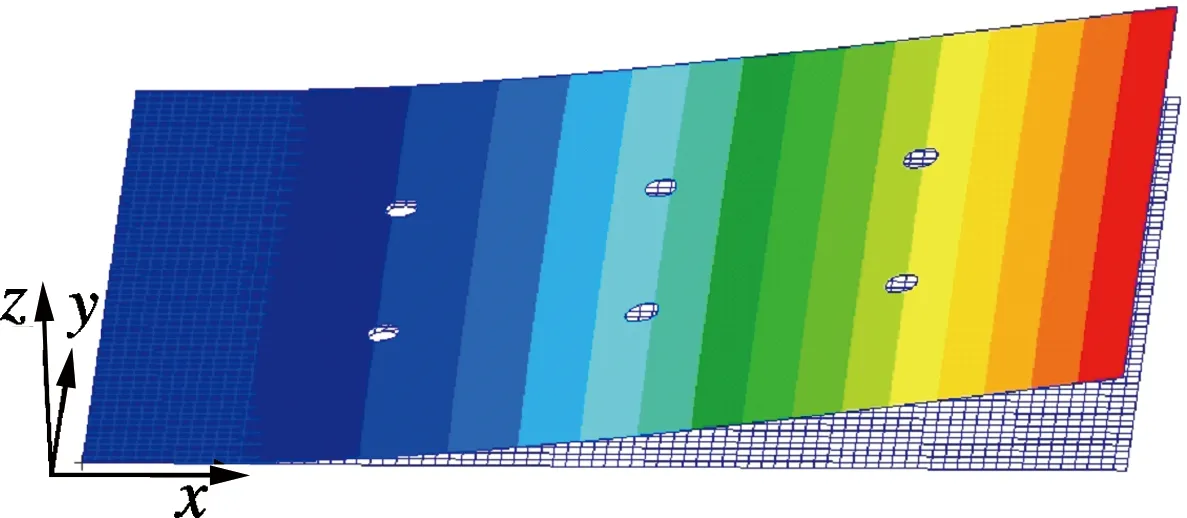
为验证所提载荷等效方法的有效性,以一开孔C/C复合材料悬臂板为研究对象,开展仿真研究．该悬臂板的有限元模型如图2所示．板尺寸为400 mm×300 mm×3 mm,板材料参数如下:x,y,z方向上的轴向拉伸模量分别为Ex=60 GPa,Ey=55 GPa,Ez=40 GPa;xy,xz,yz平面上的剪切模量分别为Gxy=32 GPa,Gxz=30 GPa,Gyz=29 GPa;xy,xz,yz平面上的泊松比分别为μxy=0.05,μxz=0.09,μyz=0.08;密度ρ=1 800 kg/m3．在一短边处30 mm范围内采用夹具夹持以实现固定约束．

图2 C/C复合材料悬臂板有限元模型(单位:mm)

2.1 模态位移频响分析

在悬臂板上表面施加单位面压载荷,分析获得板前39阶模态在0～2 000Hz内的位移,即板模态位移响应对面压载荷的频响Hip(ω),结果见图3(a)．类似地,可分析获得板模态位移响应对基础强迫位移载荷的频响Hie(ω),结果见图3(b)．

(a) 面压载荷

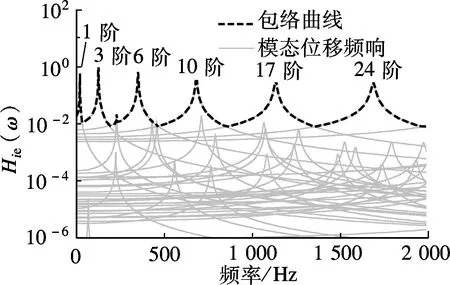
(b) 基础强迫位移载荷

图3中结果显示,在分析频段内,悬臂板第1,3,6,10,17,24阶模态对2种载荷的频响,在其固有频率附近频段内的取值远大于其余模态．这些模态在相应频段内即为主模态,板振动响应由主模态主导．图4给出悬臂板在0～2 000 Hz内各主模态振型及固有频率fi．由图可知,各主模态具有一个共同的特征:模态振型在短边方向(y轴向)的波数为零．这表明相对于其他模态,该类模态更易被面压载荷及基础强迫位移载荷激发．

2.2 载荷等效

噪声试验广泛采用中华人民共和国军用标准(GJB 150.17—86)推荐的用于噪声试验的1/3倍频程谱．本研究将该噪声1/3倍频程谱的上限转换成面压功率谱密度Spp,如图5所示(双对数坐标),其中基准功率谱密度S0为

S0=10(Lp-L0)/10

(17)

式中,Lp为噪声总声压级;L0=123.1dB．

采用式(16)计算等效载荷前,需确定各频率点处的主模态．图3中结果显示,基于模态位移对2种载荷的频响所确定的主模态存在差异．例如,由图3(a)可确定第1阶模态在多频段内为主模态, 但由图3(b)可判定第1阶模态仅在起始频段内为主模态．经比较,根据图3(b)中结果确定主模态阶次更合理．载荷等效过程中,各频率点处主模态阶次d如图6所示．

(a) 1阶，f1=20 Hz

(b) 3阶，f3=125 Hz

(c) 6阶，f6=350 Hz

(d) 10阶，f10=681 Hz

(e) 17阶，f17=1 132 Hz

(f) 24阶，f24=1 687 Hz

图5 双对数坐标下的随机面压载荷功率谱密度

在确定主模态的基础上,采用式(16)计算得到不同量级面压载荷下等效基础激励强迫位移的功率谱密度(见图7)．由图可知,在主模态发生更替的临界频率处,等效基础激励强迫位移功率谱的大小会发生突变．为考查图7中等效载荷的有效性,对载荷等效前后悬臂板上的应力响应进行了对比．

图6 不同频段内主模态的阶次

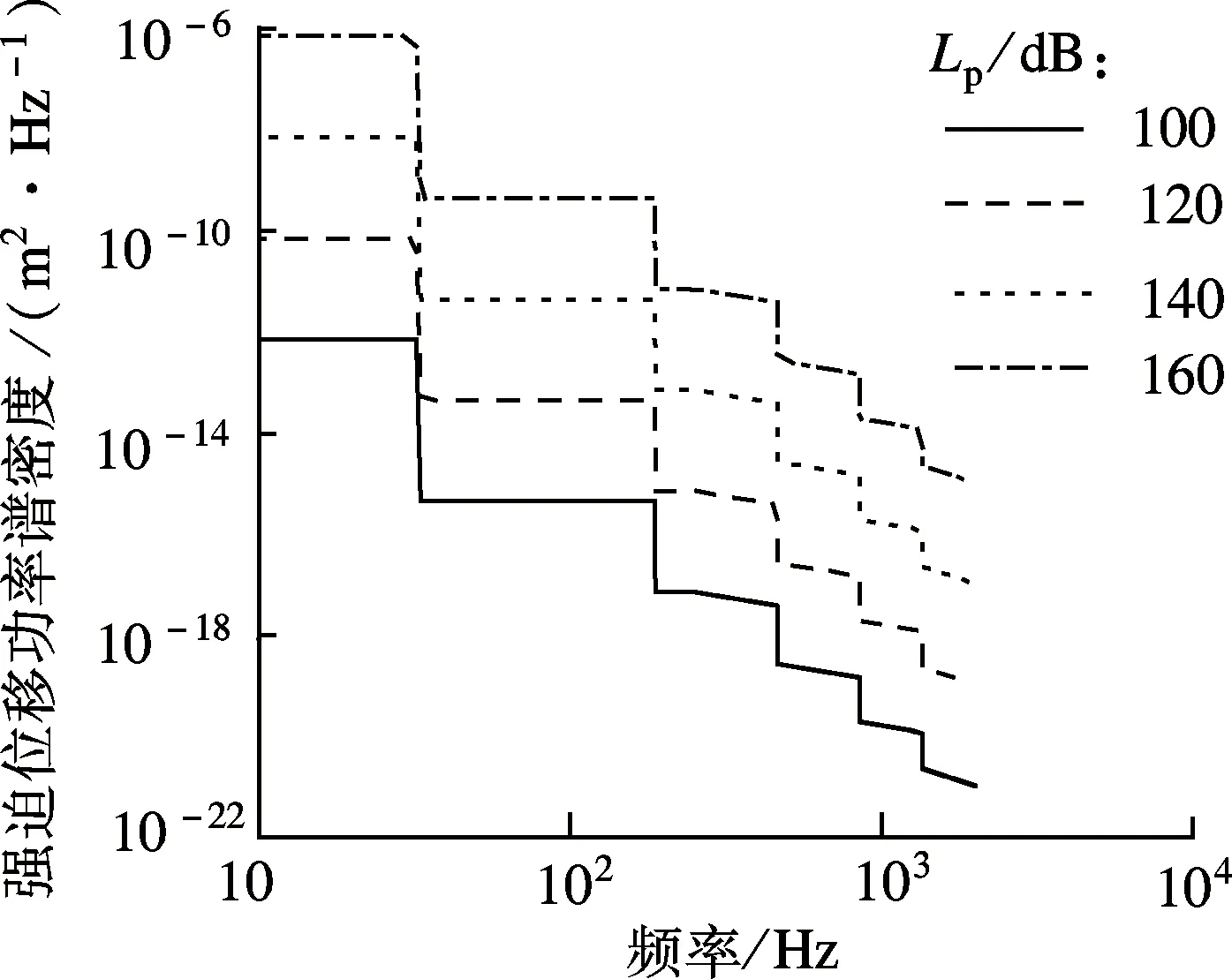
图7 等效基础激励强迫位移的功率谱密度

图8给出了等效前后2种载荷作用下板上A1，A2两个典型位置处的应力响应功率谱密度,随机面压载荷总声压级为140 dB．由图8可知,载荷等效前后板上典型位置处正应力响应的功率谱密度吻合较好,仅在远离峰值频率的频段内出现差异,该差异对应力响应均方根的影响甚微．在总声压级为140 dB的面压载荷作用下,载荷等效前后,板上A1～A5五个响应点处x轴向正应力响应在0～2 000 Hz范围内的均方根如表1所示．

(a) A1

(b) A2

图8 140 dB面压载荷等效前后板上x轴向正应力响应功率谱密度

表1 x轴向正应力响应均方根

表1中结果显示,最大应力响应出现在固支端,即危险点出现在固支端．载荷等效引起的A1～A5五个响应点处x轴向正应力响应均方根计算误差不超过2%,危险点处x轴向正应力响应均方根误差不超过1%,这对结构的强度设计及疲劳评估所产生的影响可忽略不计．图8及表1中分析结果验证了所提载荷等效方法的有效性．

3 结语

本文借助仿真分析手段,基于模态叠加法,将随机面压载荷等效为随机基础激励．该方法以主模态的位移为等效目标,忽略了其余模态对结构位移响应的贡献,将单源载荷等效这一超静定问题合理地转化为静定问题,简单易行．研究结果显示,在等效基础激励作用下,结构典型部位正应力响应功率谱密度与等效前所得结果吻合较好,所选5个响应点处x轴向正应力响应均方根误差不超过2%,危险点处x轴向正应力响应均方根误差不超过1%,从而验证了所提载荷等效方法的有效性．

References)

[1]孟光, 周徐斌, 苗军. 航天重大工程中的力学问题[J]. 力学进展, 2016, 46(1): 267-322. DOI:10.6052/1000-0992-15-018. Meng Guang, Zhou Xubin, Miao Jun. Mechanical problems in momentous projects of aerospace engineering[J].AdvancesInMechanics, 2016, 46(1): 267-322. DOI:10.6052/1000-0992-15-018.(in Chinese)

[2]Ciappi E, de Rosa S, Franco F, et al. On the dynamic behavior of composite panels under turbulent boundary layer excitations [J].JournalofSoundandVibration, 2016, 364: 77-109. DOI:10.1016/j.jsv.2015.11.024.

[3]李彦斌, 张鹏, 吴邵庆, 等. 复合材料加筋板计及热效应的声-固耦合分析[J]. 振动工程学报, 2015, 28(4): 531-540. DOI:10.16385/j.cnki.issn.1004-4523.2015.04.005. Li Yanbin, Zhang Peng, Wu Shaoqing, et al. Structural-acoustic coupling analysis of a composite stiffened panel in a thermal environment[J].JournalofVibrationEngineering, 2015, 28(4): 531-540. DOI:10.16385/j.cnki.issn.1004-4523.2015.04.005.(in Chinese)

[4]Liu L, Guo Q, He T. Thermal-acoustic fatigue of a multilayer thermal protection system in combined extreme environments [J].AdvancesinMechanicalEngineering, 2014, 6: 176891. DOI:10.1155/2014/176891.

[5]Leung K, Foist B L. Prediction of acoustically induced random vibration loads for shuttle payloads [C]//Proceedingsof36thStructures,StructuralDynamics,andMaterialsConferenceandExhibit. Washington DC, USA,1995: 1200-1208. DOI:10.2514/6.1995-1200.

[6]Lee H M. Testing for random limit load versus static limit load [R]. Huntsville, Alabama,USA: NASA, 1997.

[7]冯若强, 丁静鹄, 李庆祥, 等. 肋环型单层曲板网壳结构的风振响应及等效静风荷载[J]. 东南大学学报(自然科学版), 2012, 42(2): 328-333. DOI:10.3969/j.issn.1001-0505.2012.02.026. Feng Ruoqiang, Ding Jinghu, Li Qingxiang, et al. Wind-induced response and equivalent static wind load of single-layer geiger lattice shell with curved plate[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2012, 42(2): 328-333. DOI:10.3969/j.issn.1001-0505.2012.02.026.(in Chinese)

[8]柯世堂, 王浩. 考虑地形效应的大型电视塔等效静风荷载分析[J]. 东南大学学报(自然科学版), 2016, 46(3): 545-551. Ke Shitang, Wang Hao. Analysis on equivalent static wind loads of large television tower considering topographic effect [J].JournalofSoutheastUniversity(NaturalScienceEdition), 2016, 46(3): 545-551. (in Chinese)

[9]Ke S T, Ge Y J, Zhao L, et al. A new methodology for analysis of equivalent static wind loads on super-large cooling towers [J].JournalofWindEngineeringandIndustrialAerodynamics, 2012, 111: 30-39. DOI:10.1016/j.jweia.2012.08.001.

[10]张艳岗, 毛虎平, 苏铁熊, 等. 基于关键时间点的能量等效静态载荷法及结构动态响应优化[J]. 机械工程学报, 2016, 52(9): 151-157. DOI:10.3901/JME.2016.09.151. Zhang Yangang, Mao Huping, Su Tiexiong, et al. Energy equivalent static load method based on critical time point and structure dynamic response optimization[J].JournalofMechanicalEngineering, 2016, 52(9): 151-157. DOI:10.3901/JME.2016.09.151.(in Chinese)

[11]Rajaneesh A, Satrio W, Chai G B, et al. Long-term life prediction of woven CFRP laminates under three point flexural fatigue[J].CompositesPartB:Engineering, 2016, 91: 539-547. DOI:10.1016/j.compositesb.2016.01.028.

Equivalence method of pressure load and foundation excitation based on mode superposition technique

Zhang Peng Fei Qingguo Wu Shaoqing Li Yanbin

(School of Civil Engineering, Southeast University, Nanjing 210096, China)

The random pressure load is equivalent to the random foundation excitation based on the modal superposition method to provide evidence for the replacement of the expensive acoustic tests with the shaking table tests for thin-walled structures. The displacement of the leading modes under the two loads are required to be identical. The statically indeterminate problem of the single source load equivalence is properly simplified to a determinate problem. A carbon/carbon (C/C) composite cantilever plate is used as a research subject to investigate the validity of the load equivalence method. The results show that the power spectral density of the random stress responses at typical points of the plate under the random pressure load agrees well with that under the equivalent random foundation excitation. In the analysis of frequency band, the error of the root-mean-square (RMS) of thex-axial normal stress response at the high-risk point on the plate is less than 1%, and the errors of the RMSs of thex-axial normal stress responses at five points distributed on the plate are less than 2%. By using the proposed method, the random pressure load can be effectively equivalent to the foundation excitation, ensuring the consistency of the random stress responses on the thin-walled structures in both the frequency domain and the spacial domain when the structures are subjected to the two loads.

pressure load; foundation excitation; load equivalence; alternative test; mode superposition method

10.3969/j.issn.1001-0505.2017.02.022

2016-08-08. 作者简介:张鹏(1987—)，男，博士生；费庆国(联系人)，男，博士，教授，博士生导师，qgFei@seu.edu.cn.

国家自然科学基金资助项目(11402052，11572086)、教育部新世纪优秀人才支持计划资助项目(NCET-11-0086)、江苏省自然科学基金资助项目(BK20140616).

张鹏,费庆国,吴邵庆,等. 基于模态叠加法的面压载荷与基础激励等效方法[J].东南大学学报(自然科学版),2017,47(2):331-336.

10.3969/j.issn.1001-0505.2017.02.022.

TH113

A

1001-0505(2017)02-0331-06