行波输入下大跨度三塔悬索桥减震控制

王 浩 陶天友 张玉平 王春峰 李爱群

(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)

行波输入下大跨度三塔悬索桥减震控制

王 浩 陶天友 张玉平 王春峰 李爱群

(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)

为研究考虑行波效应的大跨度三塔悬索桥减震控制,以泰州大桥为工程背景,建立了该三塔悬索桥的有限元模型,探究了不同视波速下弹性索和黏滞阻尼器对三塔悬索桥减震效果的影响.研究结果表明:弹性索可有效控制中塔处塔梁相对位移,但边塔处塔梁相对位移可能不降反增,增幅甚至达到95.8%,若采用弹性索作为减震措施,建议只在三塔悬索桥的中塔处进行设置.在任意视波速条件下,黏滞阻尼器对各主塔塔梁相对位移均具有较好的控制效果.采用弹性索会使中塔塔底剪力呈倍数增加,而采用黏滞阻尼器时中塔塔底剪力的增幅不超过50%.因此,黏滞阻尼器比弹性索更适用于大跨度三塔悬索桥的减震控制.

三塔悬索桥;行波效应;减震控制;弹性索;黏滞阻尼器

悬索桥造型美观,传力路径明确,是当今跨越能力较大的主选桥型,尤其当需求跨径达到千米级时,悬索桥更具有绝对竞争力.然而,由于受抗风稳定性、建造难度等诸多因素的限制,传统两塔悬索桥极限跨径将小于5 km[1].为进一步提升悬索桥的跨越能力,多塔悬索桥方案成为桥梁工程界的关注重点.作为多塔悬索桥的初步尝试,21世纪前所建成的多塔悬索桥主跨均未超过300 m.对于大跨度多塔悬索桥,工程师早期通过共用锚碇将多座两塔悬索桥串联,但其本质上是多座独立受力的两塔悬索桥的组合,并非严格意义上的多塔悬索桥,其典型代表如美国奥克兰海湾大桥[2].直至2012年泰州大桥建成,多塔悬索桥才真正意义上实现由百米级向千米级的跨越.

悬索桥跨度通常较大,地震作用相对复杂,其抗震性能一直备受关注[3].对于大跨度悬索桥而言,地震波传播至各桥塔的时间并不一致,因而结构地震响应分析需考虑行波效应[4].在桥梁行波效应分析方面,国内外学者已开展很多相关的研究工作.例如,胡世德等[5]对江阴大桥进行了纵向地震响应分析,发现行波效应会增大结构关键部位的动力响应;Ettouney等[6]开展了非一致输入下大跨桥梁地震响应分析,发现行波效应会使结构内力及响应发生明显的重分配现象;Dumanoglu等[7]对大跨悬索桥行波效应进行了详细分析,发现低视波速下的主塔位移是一致输入结果的3倍.对于多塔悬索桥而言,目前国内外在结构静力非线性方面已开展了大量工作[8-9];在考虑行波效应的多塔悬索桥地震响应分析方面,相关学者也取得了一些研究成果.例如,焦常科等[10]对泰州大桥进行了地震行波效应研究,发现行波效应的影响与结构特性以及地震波特性密切相关.

桥梁减震控制是结构工程领域的又一研究重点.基于被动控制的理念,塔梁间设置弹性索或黏滞阻尼器有助于改善桥梁抗震性能,这2类减震装置已广泛应用于大跨度桥梁中.王浩等[11]以润扬大桥为背景,对比了弹性索和黏滞阻尼器对该桥地震响应的影响,并构造了阻尼器最优控制评价模型;马良喆等[12]介绍了江阴长江大桥改造工程中黏滞阻尼器的设计思路,并对阻尼器的测试内容及结果进行了详细探讨;焦常科等[13]对比了3种不同措施对三塔悬索桥的减震效果;王志强等[14]以东海大桥为背景,研究了非线性黏滞阻尼器对该桥抗震性能的影响.

上述研究工作主要围绕一致输入下的桥梁减震控制开展,对考虑行波效应的三塔悬索桥减震控制尚鲜见报道.为此,本文以泰州大桥为背景,探究了不同视波速下弹性索和黏滞阻尼器对三塔悬索桥减震效果的影响,以期为多塔悬索桥的减震分析与设计提供参考.

1 工程背景

泰州大桥总体布置如图1所示.该桥为主跨2×1 080 m的大跨度三塔悬索桥,主缆矢跨比为1∶9,两主缆横向间距为35.8 m,加劲梁采用流线型闭口扁平钢箱梁.两边塔均为混凝土结构,高178 m;中塔为钢结构,高192 m.主塔沿顺桥向均为门式框架结构,但在横桥向边塔呈单柱型,中塔呈人字形.中塔内侧壁与主梁间设置横向抗风支座,下横梁与主梁底部设置纵向弹性索,边塔处塔梁间设置竖向支座和横向抗风支座.

图1 泰州大桥整体布置图(单位:m)

2 结构有限元模型

根据泰州大桥的结构设计参数,基于ANSYS软件建立了该桥的三维有限元模型(见图2).主梁、主塔采用BEAM4单元模拟,主缆、吊杆采用LINK10单元模拟,吊杆与主梁间采用横向刚臂连接[15].采用COMBIN14单元模拟中塔下横梁与主梁间沿顺桥向设置的弹性索.根据实际支座布置,耦合边塔下横梁与主梁在横桥向、竖向及绕顺桥向的自由度,耦合中塔下横梁与主梁在横桥向及绕顺桥向的自由度.主塔底部、边缆端部均进行固接处理.

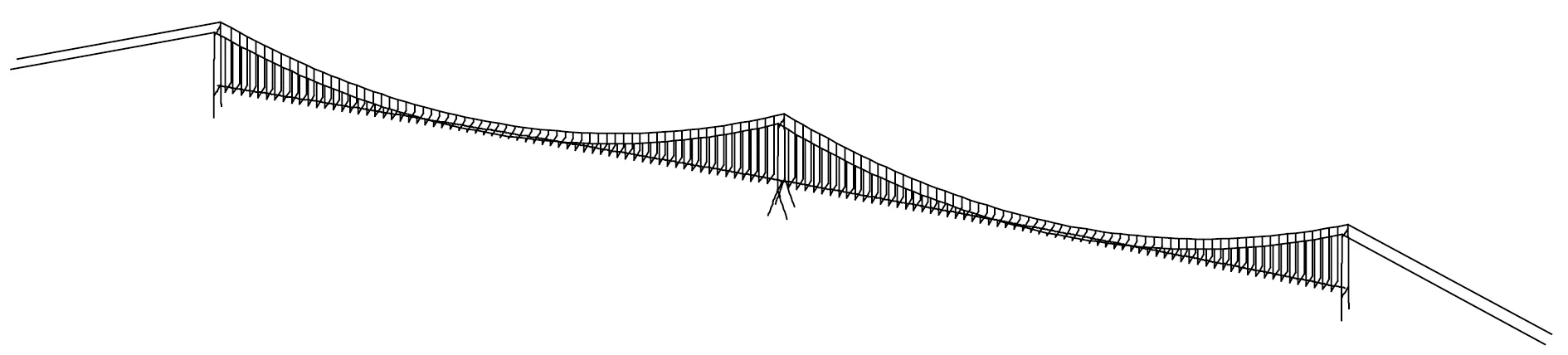
图2 三塔悬索桥有限元模型

3 三塔悬索桥地震响应分析

3.1 桥梁地震响应分析理论

按照支承点与非支承点对应的自由度进行划分后,桥梁地震响应动力分析方程可表示为[3]

(1)

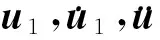
3.2 地震动输入

在三塔悬索桥地震响应分析中,考虑到结构的对称性,假定地震波沿顺桥向从左至右传播,即从泰州侧传播至扬中侧,不考虑竖向地震动作用.选取Tianjin波、ElCentro波、Taft波3条天然波作为地震动输入(三者峰值均调整为0.2g),其中Tianjin波作用下的结构响应最为突出.Tianjin波的加速度时程如图3所示.

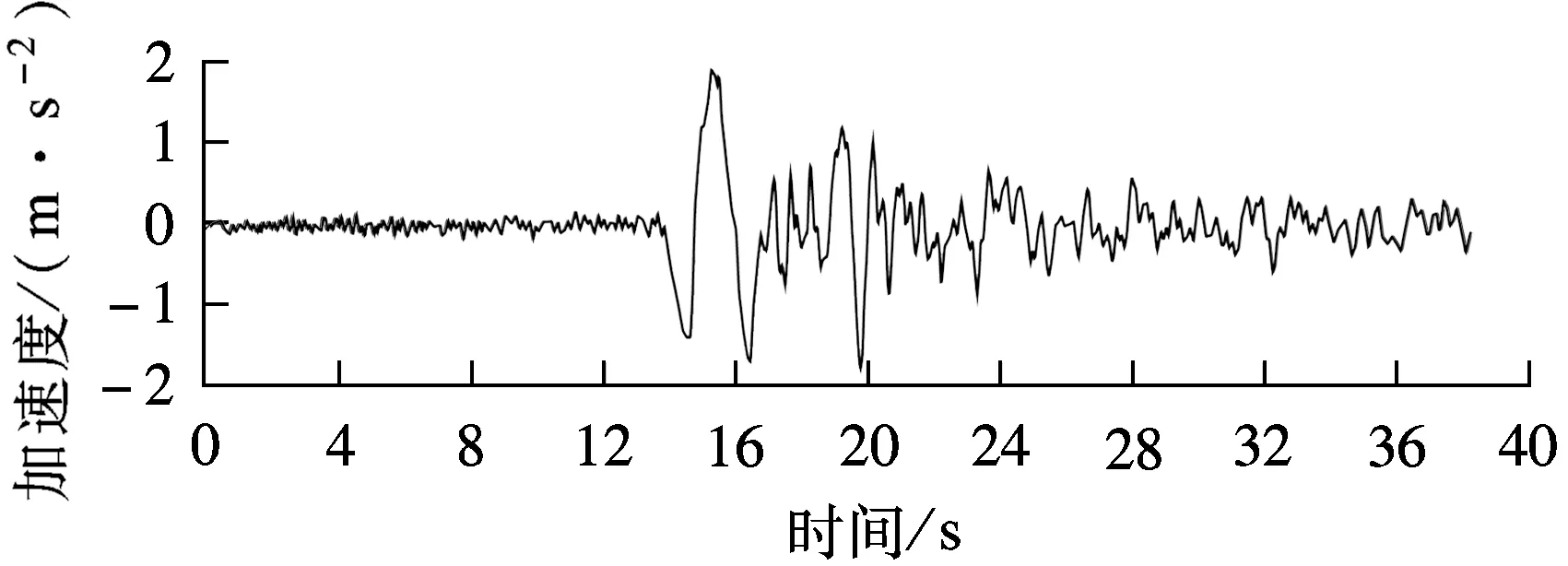
图3 Tianjin波的加速度时程

在ANSYS计算中,若将原始地震动记录直接转换为荷载时程再输入有限元模型,其塔底位移响应计算结果与加速度直接积分所得位移相差甚远(见图4(a)).为保证计算结果的准确性,本文采用线性内插的方法对地震波数据进行加密处理.由于本文重点关注结构位移响应的最大值,而当数据点加密为2n-1(n为原始地震动记录数据点数)个时,位移最大值与原始地震最大位移相差不大(见图4(b)),因此,本文实际输入的地震波为原始地震波相邻数据点进行一次等距内插所得.

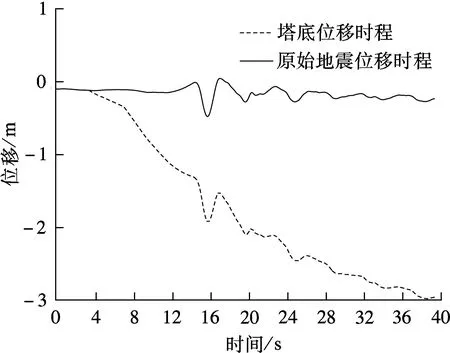
(a) 未加密地震波

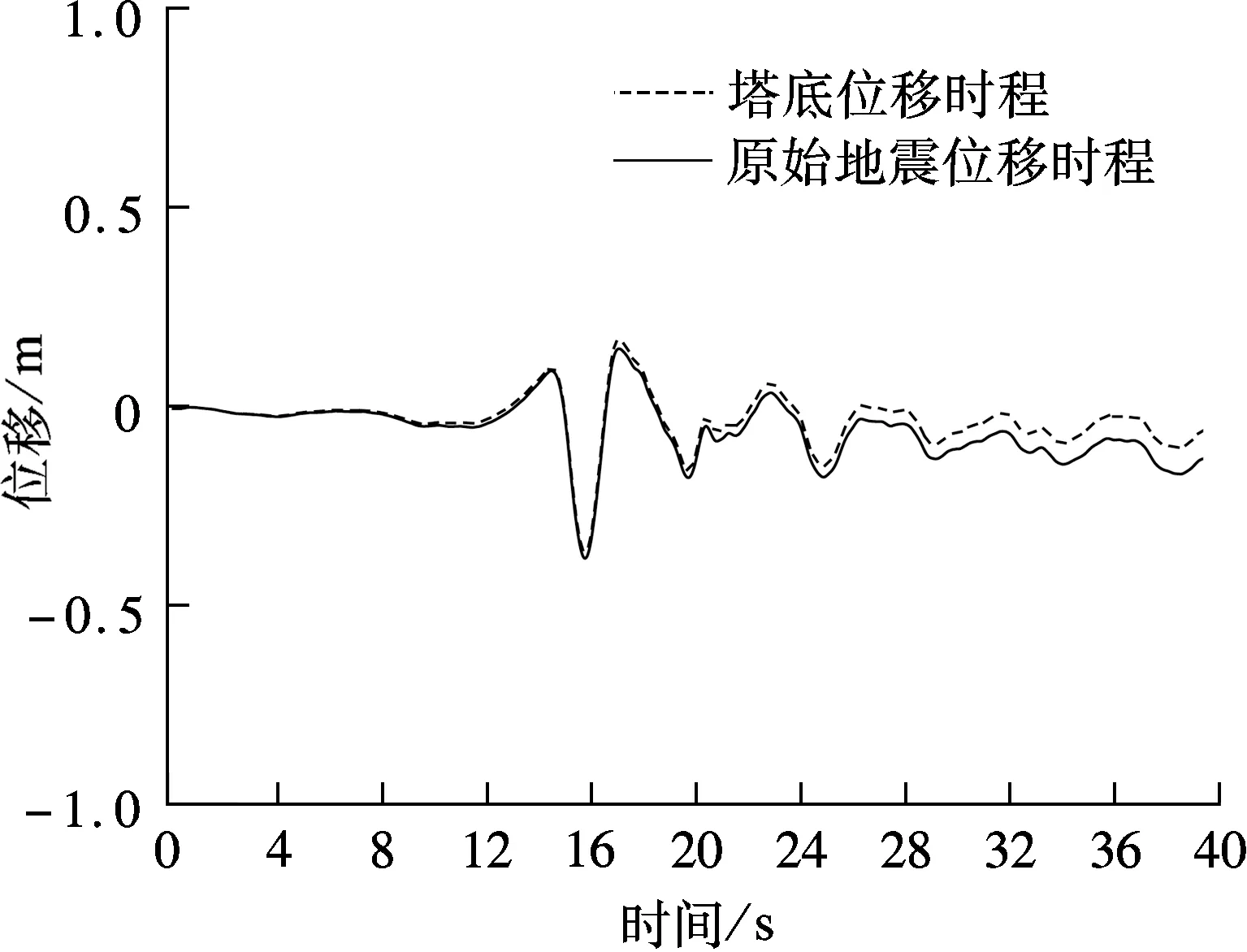
(b) 加密地震波

3.3 考虑行波效应的结构地震响应分析

采用大质量法开展了考虑行波效应的大跨度三塔悬索桥地震响应分析.视波速V=0.2,0.8,8.0 km/s时中塔处塔梁纵向相对位移时程曲线如图5所示.由图可知,视波速对中塔处塔梁相对位移峰值大小及出现时间均有影响.同时,视波速还会影响地震总持时,视波速越小,结构所受地震作用时间越长,二者关系如图6所示.文献[16]指出,在土壤、岩石等介质中,地震视波速一般在0.2～8.0 km/s范围内变化.为此,本文在该视波速范围内开展考虑行波效应的三塔悬索桥减震控制研究,以期为不同场地类型的三塔悬索桥抗震设计与分析提供参考.

图5 中塔处塔梁纵向相对位移时程曲线

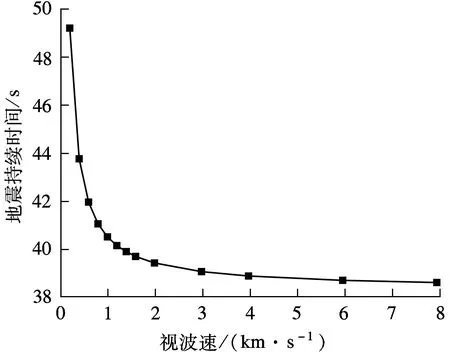
图6 视波速对地震持续时间的影响

4 考虑行波效应的桥梁减震控制

4.1 弹性索

分别在2座边塔与中塔的塔梁连接处沿纵向设置相同刚度的弹性索,研究不同视波速下弹性索刚度k对结构地震响应的影响.各主塔处的塔梁相对位移峰值如图7所示.由图可知,随着视波速的增加,边塔塔梁相对位移总体呈现先增大后减小的趋势,在0.5～1.5 km/s的范围内达到峰值.这主要因为在该范围内的视波速下,地震波从左边塔传播至右边塔的时间为1.44～4.32 s,而图3所示地震波的波峰与波谷的时间差约为1.0～4.5 s,地震波输入的反相位效应使得边塔处塔梁相对位移达到峰值.对于中塔而言,视波速对于塔梁相对位移的影响则相对较为平缓.总体而言,在高视波速条件下,各主塔处塔梁相对位移相对较小,表明刚性地基环境下三塔悬索桥的塔梁相对位移表现更优.

对于弹性索刚度对塔梁相对位移的影响,其特征主要表现为:塔梁相对位移随着弹性索刚度的增加呈先增加后减小的趋势,当弹性索刚度k为100～150 MN/m时,塔梁相对位移达到最大值.由于弹性拉索的设置可改变体系的刚度特性,通过对响应时程进行频谱分析后发现:当k为100～150 MN/m时,结构主参振型频率与Tianjin波的卓越频率接近,使得结构共振响应较为突出.为此,弹性索刚度参数的选择应避开该共振区间.

弹性索的索力与主塔底部剪力也是三塔悬索桥地震响应的重点性能指标,不同视波速下弹性索刚度对中塔弹性索索力与塔底剪力的影响分别如图8和图9所示.由图可知,不同视波速下的弹性索索力差异不大,而塔底剪力在高视波速条件下相对较小.因此,采用弹性索进行减震控制时,刚性地基对于三塔悬索桥主塔的剪力控制是有利的.在任一视波速条件下,弹性索索力与中塔塔底剪力均随着弹性索刚度的增加而增加,且增加的梯度逐渐减小.当弹性索刚度大于1 000 MN/m时,弹性索内力与中塔塔底剪力基本趋于稳定.

(a) 左边塔

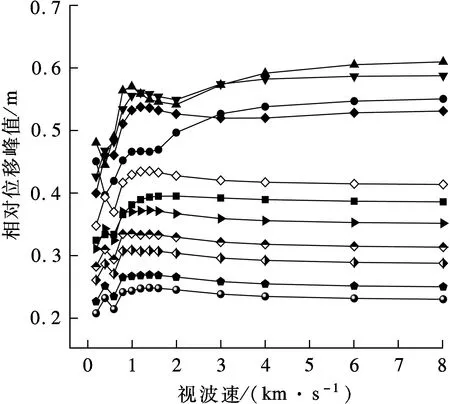
(b) 中塔

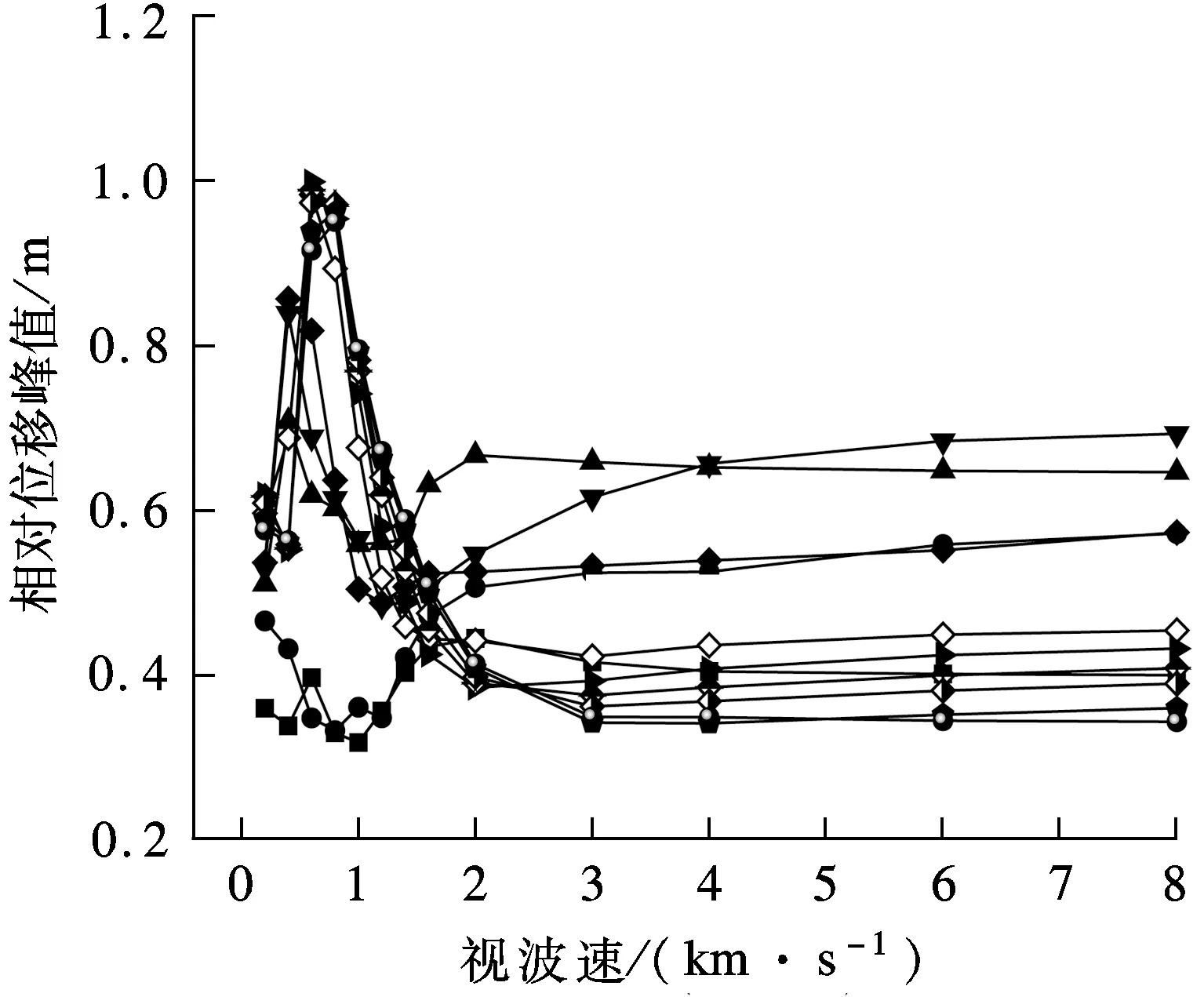
(c) 右边塔

4.2 黏滞阻尼器

分别在边塔与中塔的塔梁连接处沿纵向设置相同参数的线性黏滞阻尼器,研究不同视波速下阻尼系数c对结构地震响应的影响.各主塔处的塔梁相对位移峰值如图10所示.

图8 弹性索刚度对中塔弹性索索力的影响

图9 弹性索刚度对中塔塔底剪力的影响

由图10可知,各主塔处塔梁相对位移峰值随着阻尼系数的增加而减小.与弹性索减震工况类似,塔梁相对位移总体呈先增大再减小的趋势,但中塔与右边塔在低视波速区间(0.5～1.5 km/s)受地震波输入反相位效应影响显著,在高视波速区间(大于3.0 km/s)位移变化逐渐趋于平缓.与弹性索控制不同的是,黏滞阻尼器为速度相关型阻尼器,不会改变三塔悬索桥的动力特性,因而对塔梁相对位移的控制效果随阻尼系数的增加呈正相关变化.同时,在任意视波速条件下,黏滞阻尼器均能取得明显的减震效果.

图11和图12分别为不同视波速条件下黏滞阻尼器输出力、中塔塔底剪力随阻尼系数的变化曲线.由图可知,黏滞阻尼器输出力与中塔塔底剪力均随阻尼系数的增加而增加,但增加的梯度逐渐减小,表明高阻尼系数条件下塔梁相对速度略小于低阻尼系数条件下塔梁相对速度.对比不同视波速条件下的阻尼器输出力和塔底剪力,二者均在高视波速条件下相对较小,说明刚性地基环境对于三塔悬索桥主塔的剪力控制以及阻尼器承载是有利的.

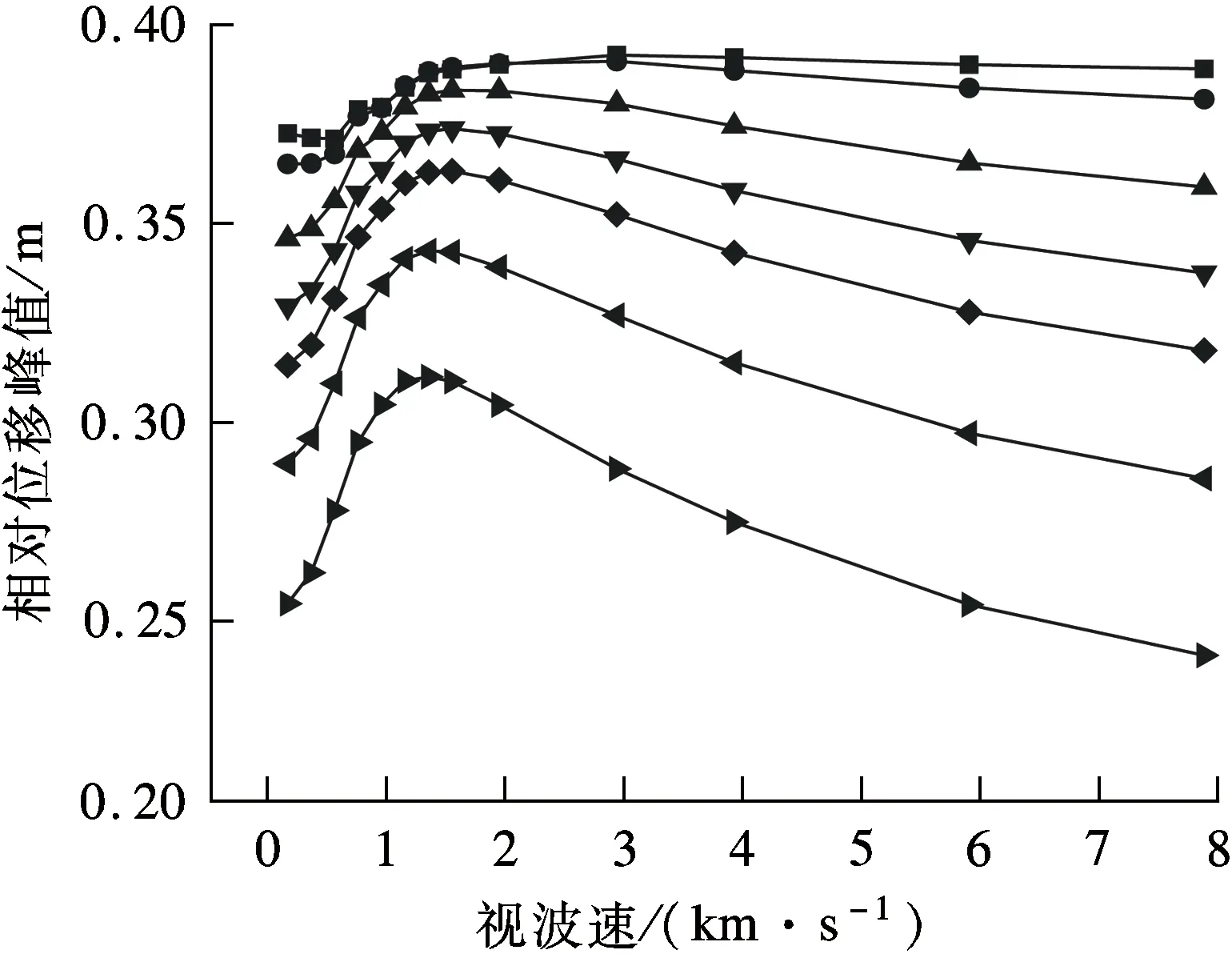
(a) 左边塔

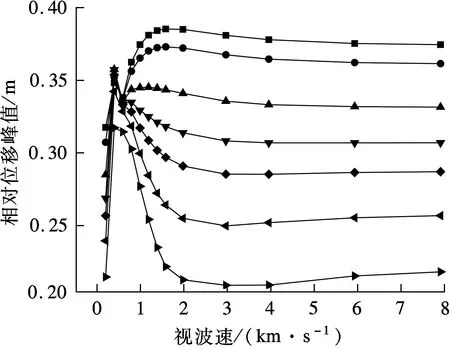
(b) 中塔

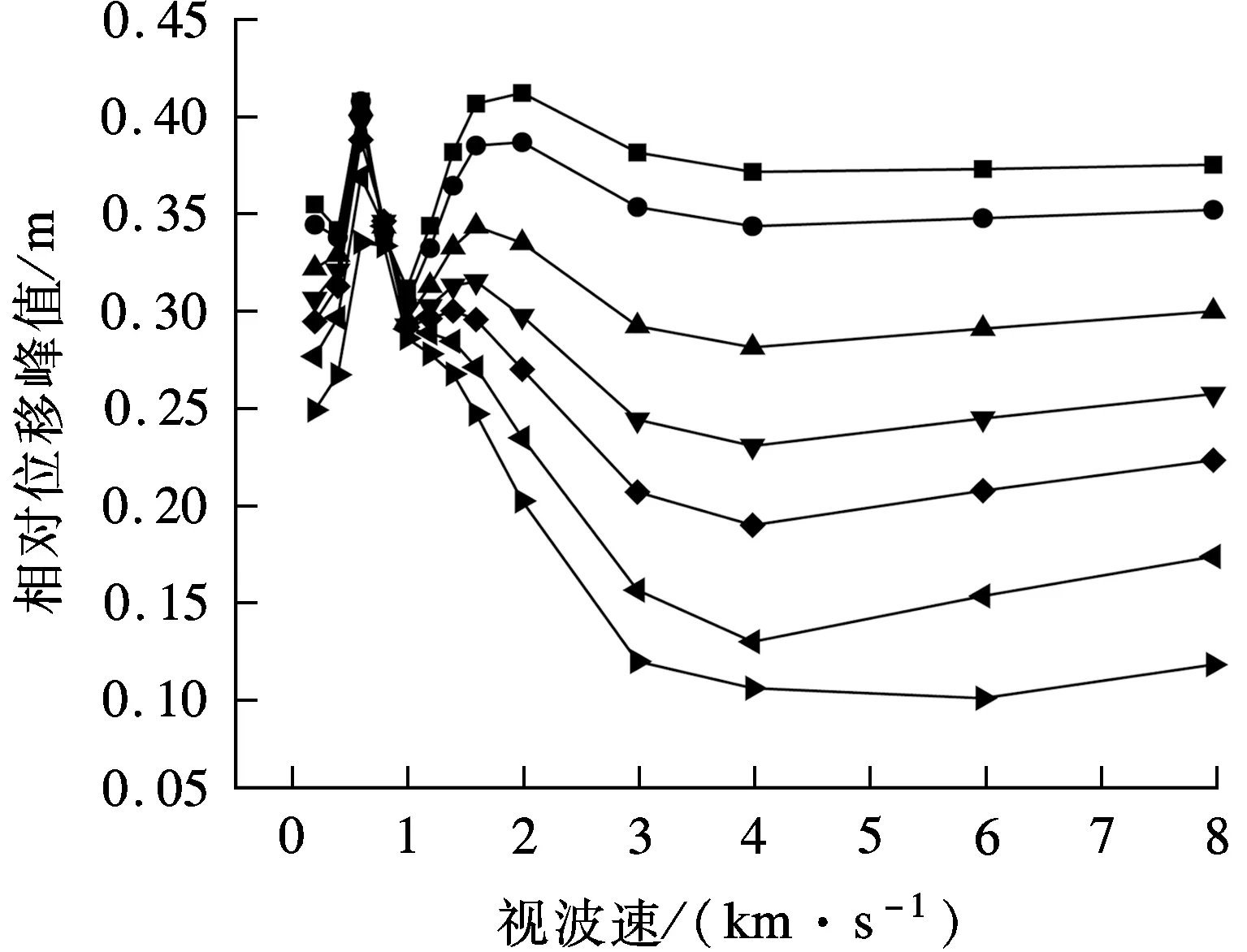
(c) 右边塔

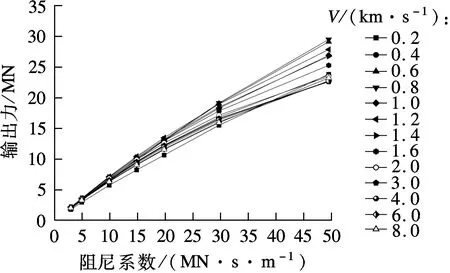
图11 黏滞阻尼器输出力随阻尼系数的变化曲线

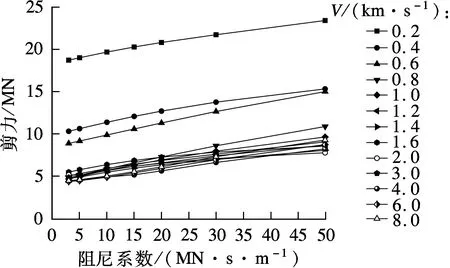
图12 中塔塔底剪力随阻尼系数的变化曲线

4.3 2种减震方案对比

为对比上述2种阻尼器在不同视波速下的减震效果,选取弹性索刚度为1 000 MN/m和黏滞阻尼器阻尼系数为15 MN·s/m两类工况进行对比,视波速分别取0.2,0.8,8.0 km/s.2种减震方案下的中塔塔梁相对位移时程曲线如图13所示.由图可知,弹性索与黏滞阻尼器均能有效控制各主塔处的塔梁相对位移,但由于弹性索改变了结构的动力特性,部分其他时刻也出现了明显峰值.

以各主塔处塔梁相对位移和中塔剪力为代表,2种减震方案下的减震率见表1.由表可知,采用弹性索可有效控制中塔处的塔梁相对位移,最大减震率可达25.4%.然而,由于弹性索的设置改变了三塔悬索桥的动力特性,边塔处塔梁相对位移不降反增,增幅甚至达到95.8%.因此,若采用弹性索作为减震措施,建议只在三塔悬索桥中塔处进行设置,这与泰州大桥所采用的方案(中塔处设弹性索)一致.对于黏滞阻尼器,在任意视波速条件下其对边塔与中塔处的塔梁相对位移均有较好的控制效果,且在中塔处的控制效果与弹性索的控制效果相当.此外,采用弹性索会使中塔塔底剪力呈倍数增加,而采用黏滞阻尼器时中塔塔底剪力的增幅在任意视波速条件下均不超过50%.因此,黏滞阻尼器比弹性索更适用于大跨度三塔悬索桥的减震控制.

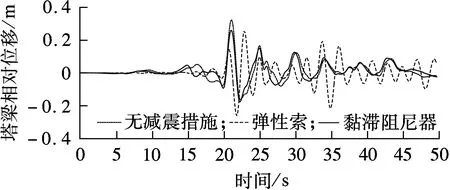
(a) V=200 m/s

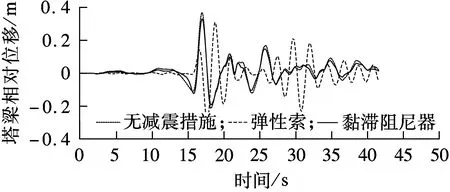
(b) V=800 m/s

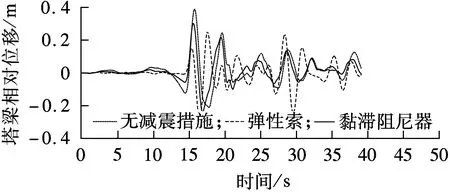
(c) V=8 000 m/s

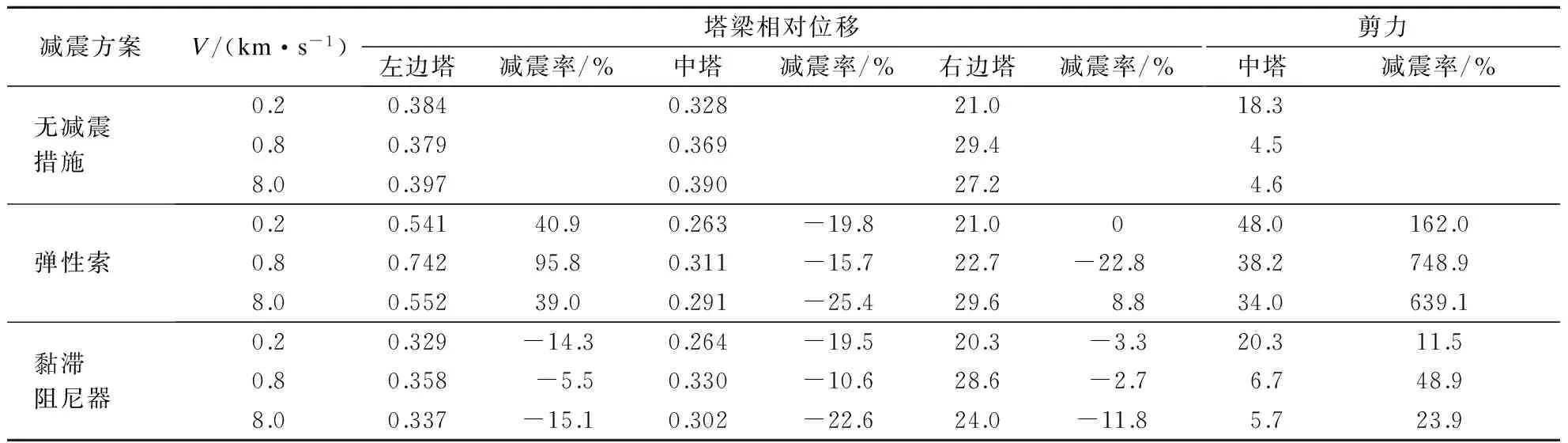
表1 不同减震方案的减震率对比

5 结论

1) 在0.5～1.5 km/s的视波速范围内,地震波输入的反相位效应使得边塔处塔梁相对位移达到峰值.在高视波速条件下,各主塔处塔梁相对位移、主塔剪力等响应相对较小且变化稳定,表明刚性地基环境对于三塔悬索桥的抗震性能更加有利.

2) 塔梁相对位移随弹性索刚度的增加呈先增加后减小的趋势.当弹性索刚度为100～150 MN/m时,塔梁相对位移达到最大值.由于弹性索的设置改变了结构动力特性,结构主参振型频率与Tianjin波卓越频率接近,从而导致结构共振响应较突出.因此弹性索刚度参数的选择应避开该共振区间.

3) 塔梁相对位移随着阻尼系数的增加而减小.与弹性索控制不同的是,黏滞阻尼器为速度相关型阻尼器,不会改变三塔悬索桥的动力特性,因而对塔梁相对位移的控制效果随阻尼系数的增加呈正相关变化.在任意视波速条件下,黏滞阻尼器均能取得明显的减震效果.

4) 弹性索可有效控制中塔处塔梁相对位移,但对边塔处塔梁相对位移的控制效果不降反增,增幅甚至达到95.8%.因此,若采用弹性索作为减震措施,建议只在三塔悬索桥的中塔处进行设置.

5) 在任意视波速条件下,黏滞阻尼器对各主塔塔梁相对位移均有较好的控制效果.采用弹性索会使中塔塔底剪力呈倍数增加,而采用黏滞阻尼器时中塔塔底剪力增幅不超过50%.因此,黏滞阻尼器比弹性索更适用于大跨度三塔悬索桥的减震控制.

References)

[1]葛耀君. 大跨度悬索桥抗风[M]. 北京: 人民交通出版社, 2011: 530-544.

[2]陶天友. 大跨度三塔连跨悬索桥风致抖振及其MTMD控制研究[D]. 南京: 东南大学土木工程学院, 2015.

[3]范立础. 桥梁抗震[M]. 上海: 同济大学出版社, 1997: 155-158.

[4]何庆祥, 沈祖炎. 结构地震行波效应分析综述[J]. 地震工程与工程振动, 2009, 29 (1): 50-57. He Qingxiang, Shen Zuyan. Review of structural seismic analysis of travelling wave effects[J].JournalofEarthquakeEngineeringandEngineeringVibration, 2009, 29(1): 50-57. (in Chinese)

[5]胡世德, 范立础. 江阴长江公路大桥纵向地震反应分析[J]. 同济大学学报(自然科学版), 1994, 22(4): 434-438. Hu Shide, Fan Lichu. The longitudinal earthquake response analysis for the Jiangyin Yangtze river bridge[J].JournalofTongjiUniversity(NaturalScienceEdition), 1994, 22(4): 434-438. (in Chinese)

[6]Ettouney M, Hapij A, Gajer R. Frequency-domain analysis of long-span bridges subjected to nonuniform seismic motions[J].JournalofBridgeEngineering, 2001, 6(6): 577-586. DOI:10.1061/(asce)1084-0702(2001)6:6(577).

[7]Dumanoglu A A, Brownjohn J M W, Severn R T. Seismic analysis of the Fatih Sultan Mehmet (second Bosporus) suspension bridge [J].EarthquakeEngineeringandStructuralDynamics, 1992, 21(10): 881-906. DOI:10.1002/eqe.4290211004.

[8]Yoshida O, Okuda M, Moriya T. Structural characteristics and applicability of four-span suspension bridge[J].ASCEJournalofBridgeEngineering, 2004, 9(5): 453-463. DOI:10.1061/(asce)1084-0702(2004)9:5(453).

[9]Choi D H, Gwon S G, Yoo H, et al. Nonlinear static analysis of continuous multi-span suspension bridges[J].InternationalJournalofSteelStructures, 2013, 13(1): 103-115. DOI:10.1007/s13296-013-1010-0.

[10]焦常科, 李爱群, 操礼林, 等. 三塔悬索桥行波效应研究[J]. 土木工程学报, 2010, 43(12): 100-106. Jiao Changke, Li Aiqun, Cao Lilin, et al. Traveling wave influence analysis for triple-tower suspension bridges[J].ChinaCivilEngineeringJournal, 2010, 43(12): 100-106. (in Chinese)

[11]王浩, 李爱群, 郭彤. 超大跨悬索桥地震响应的综合最优控制研究[J]. 湖南大学学报(自然科学版), 2006, 33(3): 6-10. DOI:10.3321/j.issn:1000-2472.2006.03.002. Wang Hao, Li Aiqun, Guo Tong. Compositive optimal control of the seismic response for super-long-span suspension bridges[J].JournalofHunanUniversity(NaturalSciences), 2006, 33(3): 6-10. DOI:10.3321/j.issn:1000-2472.2006.03.002. (in Chinese)

[12]马良喆, 陈永祁. 江阴长江大桥用液体粘滞阻尼器的测试鉴定和结果初分析[J]. 建筑结构, 2007, 37(S1): 1-4. Ma Liangzhe, Chen Yongqi. Testing and result analysis of the fluid viscous dampers for Jiangyin Bridge[J].BuildingStructure, 2007, 37(S1):1-4. (in Chinese)

[13]焦常科, 李爱群, 王浩. 三塔悬索桥地震响应控制[J]. 振动、测试与诊断, 2011, 31(2): 156-161. DOI:10.3969/j.issn.1004-6801.2011.02.004. Jiao Changke, Li Aiqun, Wang Hao. Seismic response control for triple-tower suspension bridges[J].JournalofVibration,Measurement&Diagnosis, 2011, 31(2): 156-161. DOI:10.3969/j.issn.1004-6801.2011.02.004.(in Chinese)

[14]王志强, 胡世德, 范立础. 东海大桥粘滞阻尼器参数研究[J]. 中国公路学报, 2005, 18(3): 37-42.DOI：10.3321/j.issn:1001-7372.2005.03.008. Wang Zhiqiang, Hu Shide, Fan Lichu. Research on viscous damper parameters of Donghai Bridge[J].ChinaJournalofHighwayandTransport, 2005, 18(3):37-42. DOI：10.3321/j.issn:1001-7372.2005.03.008.(in Chinese)

[15]陶天友, 王浩, 李爱群. 中塔对大跨度三塔连跨悬索桥抖振性能的影响[J]. 振动、测试与诊断, 2016, 36(1): 131-137.DOI:10.16450/j.cnki.issn.1004-6801.2016.01.022. Tao Tianyou, Wang Hao, Li Aiqun. Influence of mid-tower on the buffeting performance of a long-span triple-tower suspension bridge with continuous span[J].JournalofVibration,Measurement&Diagnosis, 2016, 36(1): 131-137. DOI:10.16450/j.cnki.issn.1004-6801.2016.01.022.(in Chinese)

[16]陆基孟. 地震勘探原理(上册)[M]. 东营: 石油大学出版社, 2001: 189-190.

Seismic control of long-span triple-tower suspension bridge under travelling wave action

Wang Hao Tao Tianyu Zhang Yuping Wang Chunfeng Li Aiqun

(Key Laboratory of Concrete and Pre-stressed Concrete Structure of Ministry of Education, Southeast University, Nanjing 210096, China)

To study the seismic control of a long-span triple-tower suspension bridge considering the travelling wave effect, the Taizhou Bridge was taken as a research object and a finite element model of this bridge was established. The influences of the elastic cable and the viscous damper on the seismic control efficiency with different apparent wave velocities were investigated. The results show that the elastic cable can effectively control the relative displacement between the main girder and the mid-tower, but the displacement at the side-tower has an increase up to 95.8% instead of a decrease. If the elastic cable is utilized, it is suggested to be installed only at the mid-tower. At any apparent wave velocity, the viscous damper exhibits good control efficiency to the relative displacement between the main girder and the mid-tower. The shear force at the bottom of the mid-tower increases in multiples with the adoption of the elastic cable,while it increases no more than 50% with the utilization of the viscous damper. Therefore, the viscous damper is more suitable than the elastic cable in the seismic control of a long-span triple-tower suspension bridge.

triple-tower suspension bridge; travelling wave effect; seismic control; elastic cable; viscous damper

10.3969/j.issn.1001-0505.2017.02.024

2016-05-21. 作者简介: 王浩(1980—)，男，博士，研究员，博士生导师， wanghao1980@seu.edu.cn.

国家重点基础研究发展计划(973计划)青年科学家专题资助项目(2015CB060000)、国家自然科学基金资助项目(51278104，51578151)、中央高校基本科研业务费专项资金资助项目(2242015K42028)、东南大学优秀博士学位论文培育基金资助项目(YBJJ1659).

王浩，陶天友,张玉平,等：行波输入下大跨度三塔悬索桥减震控制[J].东南大学学报(自然科学版),2017,47(2):343-349.

10.3969/j.issn.1001-0505.2017.02.024.

U441;U448.27

A

1001-0505(2017)02-0343-07