基于环境变量建模的锂电池SOC估计方法

刘新天 孙张驰 何 耀 郑昕昕 曾国建

(合肥工业大学新能源汽车工程研究院, 合肥 230009)

基于环境变量建模的锂电池SOC估计方法

刘新天 孙张驰 何 耀 郑昕昕 曾国建

(合肥工业大学新能源汽车工程研究院, 合肥 230009)

通过对不同温度和锂电池荷电状态(SOC)下电池内部参数测定和评估,分析了影响参数变化的环境因素,建立了可变参数的锂电池Thevenin模型．讨论了模型的分段依据以及相关参数的测定和拟合方法,并采用扩展卡尔曼滤波算法(EKF)对锂电池SOC进行估算,给出了基于温度修正的改进SOC估计方法．所提出的电池模型解决了现有算法中模型适用范围局限性的问题,仿真和实验结果表明,所建立的基于锂电池Thevenin模型的SOC估计方法在较宽的温度范围内都能够获得较高的估算精度．

动力锂电池;荷电状态;温度补偿;Thevenin模型; 扩展卡尔曼滤波

锂电池具有高功率密度、高单体电压等优点,是常用的电动汽车动力来源[1-2]．锂电池荷电状态(SOC)的精确估计,对保障电池组安全性和续航能力有着重要的意义[3]．然而,电动汽车复杂的运行工况给SOC的精确估计带来了较大的困难,目前常用的安时积分法存在积分初值难以判断、采样误差大以及噪声干扰等问题[4],导致SOC估算精度低,且估算误差会随时间累加．开路电压法估计耗时较长并且不适用于实时电量估计,为解决该问题,文献[5]提出了一种基于电池等效电路模型的非稳态开路电压方法．卡尔曼滤波算法估计 SOC 的核心包含SOC估计值和反映估计误差的协方差矩阵的递归方程,协方差矩阵给出估计误差范围．目前常用的扩展卡尔曼滤波算法(EKF)[6-7]、无迹粒子滤波(UPF)算法的SOC估算方法都是根据此原理来提高安时积分法的估算精度．观测方程能否有效地矫正状态方程误差,很大程度上取决于锂电池模型能否与实际电池特性相一致[8],因此,锂电池模型的精确性是提高SOC估算精度的关键．

目前常用的锂电池等效电路模型有Rint模型、RC模型、Thevenin模型和PNGV模型等[9-12]．其中，Thevenin模型具有物理意义明确、模型参数辨识实验容易执行等优点,被广泛应用于电池的数学建模中[13],但其参数固定,无法反映电池动态特性．对此问题,文献[14]提出了带可变参数锂离子电池Thevenin模型的改进方法,探讨了电池模型相关参数和SOC的关系．文献[15]分析了动力锂电池的温度特性,对建立考虑温度影响的电池模型具有重要的参考价值．

现有的SOC估计方法中,针对电池的建模很少考虑环境尤其是温度的影响,实际上,电池模型的参数随环境温度的变化而变化,其可用容量在不同温度条件下差别很大,因此温度在很大程度上影响着电池模型的精确度,进而影响SOC的估计精度．文献[16]提出了基于无迹卡尔曼滤波的动力电池SOC估计方法,通过温度补偿系数对SOC进行修正;文献[17]提出了一种锂离子电池低温SOC估计算法,直接通过安时积分结果对不同温度下估算的SOC进行换算．对于上述方法,温度的影响直接作为SOC估计的修正因子,其对电池模型的影响仍需进一步研究．

针对上述问题,本文提出了基于环境变量建模的锂电池SOC估计方法,综合考虑温度和SOC等因素的影响,将锂电池Thevenin模型中欧姆内阻、极化内阻、极化电容等参数定义为环境变量的函数,并通过混合动力脉冲能力特性(HPPC)实验[18]辨识模型参数．首先通过测试和计算得到电池模型实际参数值,并以此为依据确定模型的参数拟合方法,最后通过仿真和实验验证了锂电池模型的准确性和SOC的估算精度．

1 可变参数的锂电池Thevenin模型

根据Thevenin模型,锂电池内部的极化电容Cpol和极化电阻Rpol相并联,并与表征开路电压的直流电压源Uoc和欧姆内阻Rohm串联组合．其中Cpol，Rpol，Rohm均为可变参数,与电池SOC和温度等环境因素有关.由于电池内阻中除欧姆内阻和极化内阻之外的其他内阻很小,相对于欧姆内阻可以忽略不计,因此在建立电池模型时可以不计其他内阻对模型的影响．等效电池模型如图1所示,由此可得到电池开路电压Uoc和端电压UB的关系式为

Uoc=U1+RohmIB+UB

(1)

式中,IB为电池的充放电电流,参考方向如图1所示;U1为Rpol和Cpol两端的电压,定义为电池的超电势,其表达式为

(2)

图1 锂电池等效模型

2 基于环境变量的锂电池数学模型

2.1 参数测定方法

由于无法直接测得图1中的电阻、电容等参数,需要通过实际检测到的参数进行计算．欧姆内阻Rohm等于欧姆电压ΔUohm和充放电电流IB的比值;极化内阻Rpol等于极化电压ΔUpol和充放电电流IB的比值．其中,ΔUohm和ΔUpol可由HPPC实验得到[18],实验对象为额定电压3.2 V,额定容量为9 A·h的国轩圆柱形磷酸铁锂电池．图2给出了HPPC实验电流电压波形,每个测试周期Ts内分别给予电池负向和正向的脉冲电流．

图2 HPPC实验电流电压波形

由于欧姆内阻的存在,电池充放电过程中会产生瞬间电压变化,因此脉冲电流结束后电压直接跳变为欧姆电压ΔUohm;由于极化内阻的存在,停止充放电后,电压经历急速变化后趋于稳定,因此电压滞后变化的量即为极化电压ΔUpol．取正、负向放电测得电压的平均值作为测试值,可得到欧姆内阻Rohm和极化内阻Rpol表达式为

(3)

由Rpol可计算出极化电容Cpol,即

(4)

式中,τ为电池极化过程时间常数．

图3给出了SOC为90%时的锂电池在-20,20,56 ℃下的HPPC实验电压特性曲线.可以看出,电池端电压在不同温度下具有较大的差异,说明温度对电池相关参数影响较大.而根据现有研究,SOC对电池参数也有一定的影响,因此,在建立电池数学模型时需要将温度和SOC作为环境因素进行考虑．

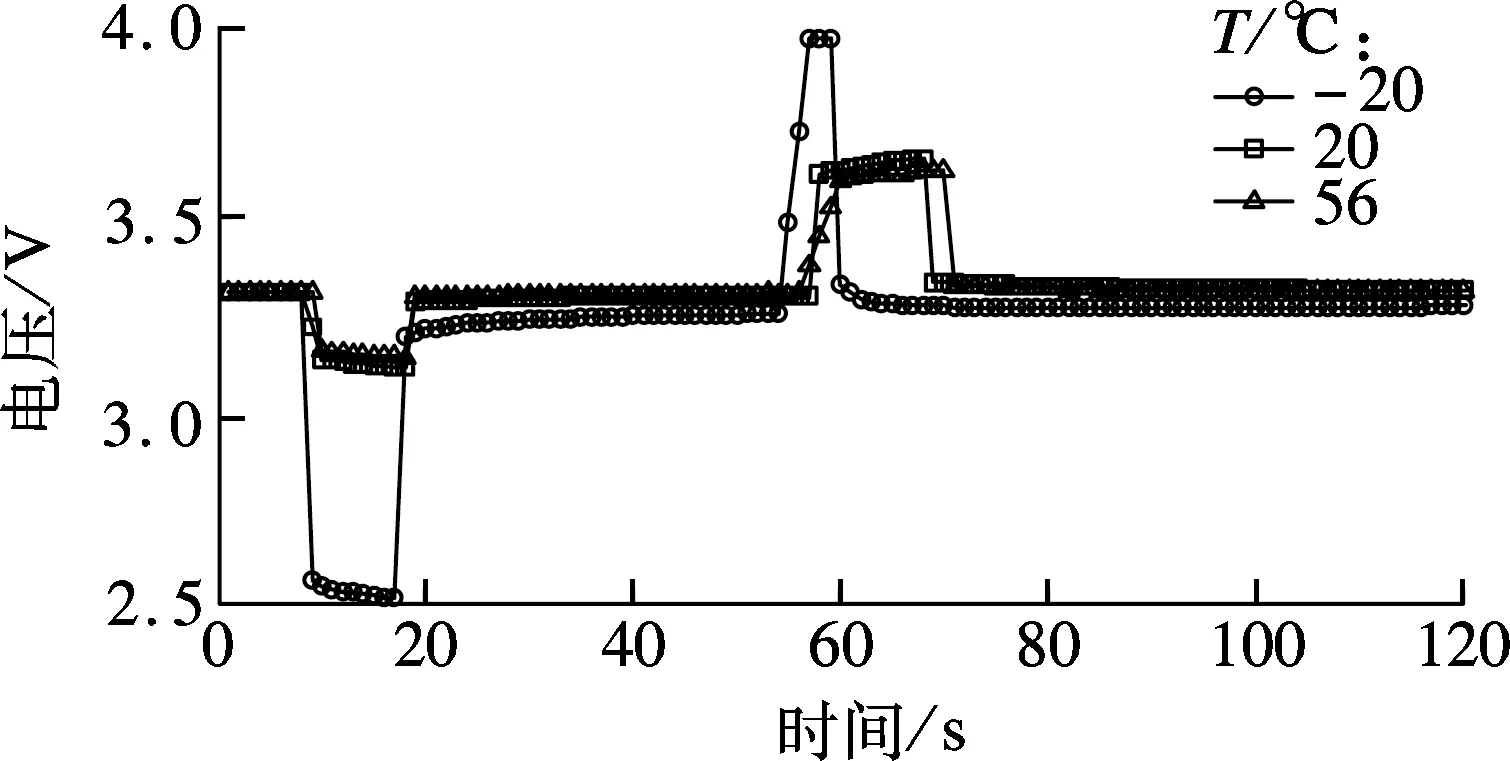
图3 不同温度下SOC为90%时电池端电压特性比较

经过多次HPPC实验,获取不同SOC状态下各温度点对应的电压和电流值,利用离散数据曲线拟合方法得到各参数与环境因素的函数关系．图4给出了测定的欧姆电阻和环境因素关系,由图可见,Rohm随温度的降低而升高;当SOC<30%时,Rohm会突然升高,而当SOC>30%时,SOC对Rohm的影响并不明显,在SOC为30%～50%时Rohm比SOC>50%的Rohm略高．图4为分段拟合的区域划分提供了依据．

(a) Rohm和SOC,T的关系

(b) 典型SOC下Rohm和T的关系

(c) 典型温度下Rohm和SOC的关系

在图4的基础上研究分段区间的划分,可以看出SOC影响较大的区间在0～30%范围内,可以在此区域内继续分段,图5给出了2种不同拟合区域划分的比较.分析拟合曲线很明显看出，区间划分越多，拟合精度越高,但是同时会增大建模实验量和SOC估计的复杂度.若将区间划分为3段,则在SOC较低时估算会存在很大误差；若将区间划分为5段,会得到很好的拟合精度,但是模型复杂度较高,需要很大的实验量来辨识模型参数．综合考虑精度的允许范围和模型复杂度,最终确定划分为4个区间．

(a) 3段拟合区域划分

(b) 4段拟合区域划分

2.2 基于分段SOC的参数拟合

根据上文的分析,可将SOC分为[10%,15%)、[15%,30%)、[30%,50%)、[50%,100%]四个区域,并取这4个区域对应的Rohm-T关系进行拟合.当SOC<10%时,估算误差较大,但在实际使用中,由于放电末端电池压降明显,且锂电池的不一致性的影响,部分电池可能会提前到达放电截止电压．为了防止电池过放电对电池寿命造成影响，在电动汽车运行过程中,锂电池很少出现SOC<10%电量,故本文中不予考虑SOC<10%的情况．当电池SOC>90%时,内阻基本不变．

拟合后各个参数的表达式为

(5)

式中,a0～a11为系数，具体拟合值见表1．

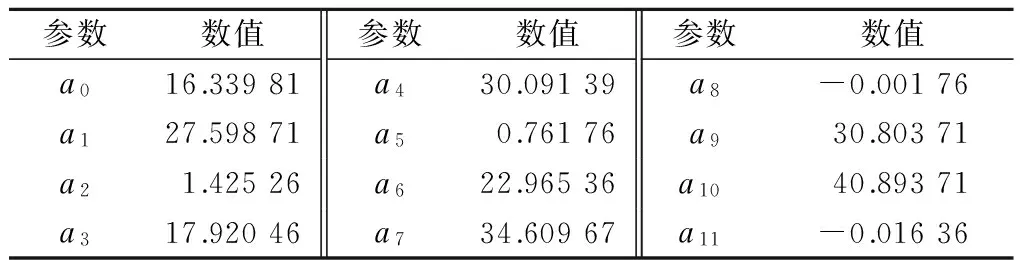
表1 Rohm参数辨识

图6给出了拟合得到的欧姆电阻和环境因素的关系,在每个划分的区域范围内,可近似认为SOC对Rohm没有影响，所拟合的Rohm表达式在实际应用中具有较高的准确度．拟合后的欧姆内阻最大误差为7.4 mΩ,相对于固定模型有很大的改善．

图6 拟合的欧姆电阻和环境因素关系

同理可对Rpol进行拟合,其表达式为

(6)

式中b0～b11为系数，具体拟合值见表2．

表2 Rpol参数辨识

电池停止放电后,经历3τ后电池极化电压衰减95%,从测试数据可以得到τ值，如表3所示．

表3 Cpol参数辨识

由此可得到Cpol表达式为

(7)

由于电池充放电运行过程中电池开路电压不可测,因此通过EKF的观测过程证明模型的优化效果．

3 基于EKF的SOC估算方法

3.1 观测方程的建立

锂离子动力电池的数学模型是估算电池SOC的基础,通过所建立的模型能够得到电池的观测方程．该方程描述了SOC、充放电电流、温度等因素与电池端电压的函数关系[19-20]．

放电过程中SOC状态方程为

(8)

式中,SOC(t)为t时刻的瞬时SOC值;SOC(0)为初始SOC值;i(t)为t时刻瞬时电流值;Qreal为电池可用总容量．

定义Qfull为电池额定容量,η为比例系数,用于补偿放电速率、温度等因素对电池总容量的影响,则Qfull和Qreal的关系可以表示为

(9)

根据上文所建立的动态系统Thevenin模型,可得到电池非线性状态空间模型的观测方程为

UB(SOC,T)=Uoc(SOC)-U1(SOC,T)-

Rohm(SOC,T)×IB

(10)

式中,UB(SOC,T)为电池端电压;Uoc(SOC)为不同SOC下的电池开路电压;U1(SOC,T)为不同环境下电池超电势;Rohm(SOC,T)为不同环境下电池欧姆内阻．

在EKF算法中,电池模型的状态变量xk为唯一变量,表征第k次计算得到的SOC值;观测变量yk表征通过电池模型第k次计算得到的电池端电压UB;输入变量ik表征第k次计算时的电池充放电电流IB．将式(8)、(10)离散化可得电池的离散状态空间模型为

(11)

yk=Uoc(xk)-U1(xk,T)-Rohm(xk,T)ik+vk

(12)

式中,Δt为采样周期;wk为系统噪声,vk为观测噪声,二者为不相关的零均值Gauss白噪声.将EKF算法用于电池SOC估计时,首先建立如式(11)、(12)所示的电池离散状态空间模型,进而完成初始值设定、更新、测量更新以及计算卡尔曼增益等步骤,实现对状态变量的最小方差估计,最后对状态方程的输出结果实现滤波,得到具有较高精度的SOC估计值[21]．

3.2 改进的SOC估算方法

在传统基于EKF的SOC估计方法中,电池的可用总容量Qreal被看作恒定值,实际上,环境温度会影响Qreal,进而对SOC估计值的精度产生影响．为探讨温度对Qreal的影响,在(20±5) ℃环境温度下对充满电的电池静置1 h后,以3 A恒流放电至电压下限停止,放出的容量为电池额定容量．在不同环境温度下电池能够放出的实际容量不同于额定容量．因此,引入温度补偿系数ηT来表征不同温度下电池实际容量与电池额定容量之间的关系,即

Qreal=ηTQfull

(13)

通过式(9)、(13)可得

(14)

可以看出,电池总容量是电池SOC估算的重要变量,ηT反映了环境温度与电池总容量的对应关系,即可通过ηT补偿电池SOC估算值．

为辨识出温度补偿系数ηT与组合模型各个系数,分别在-20,-10,0,10,20,30和40 ℃时以3 A电流放电,放电至截止电压后停止放电,可得出各温度对应的容量图,如图7所示．

图7 锂电池容量-温度变化

根据图7中温度对应电池可用容量变化趋势进行拟合,得到如下公式:

(15)

式中，a,b,c为模型参数,通过实验辨识出的参数值如表4所示．

表4 温度补偿系数参数辨识

将式(13)、(15)代入式(8),可得到改进的状态方程,再根据EKF算法对SOC进行估计,提高了SOC估计值的准确度．

4 仿真实验及结果验证

为验证引入温度补偿系数ηT对提高电池SOC估计精度的作用,选取额定容量9 A·h的锂电池组作为实验对象．该电池组共由12只单体9 A·h的磷酸铁锂电池串联而成,依据道路电动车辆用锂离子蓄电池测试标准规定的模拟工况对电池组进行放电实验．然后，进行建模仿真,将估计的SOC值与实际放电测得的真实SOC值进行比较．图8为放电电流波形．

图8 模拟工况放电电流

以上述放电实验中得到的放电电流、电池端电压数据为基础,计算出-14,10和30 ℃下的温度补偿系数ηT,在Matlab中将引入温度补偿系数修正的SOC估计值与实际测量的真实SOC值进行比较，结果如图9～图11所示． 其中EKF1是引入环境变量的SOC估计值,EKF2是未引入环境变量的SOC估计值,EKF3是未引入环境变量和容量修正的SOC估计值．

(a) SOC估计曲线与实际SOC曲线

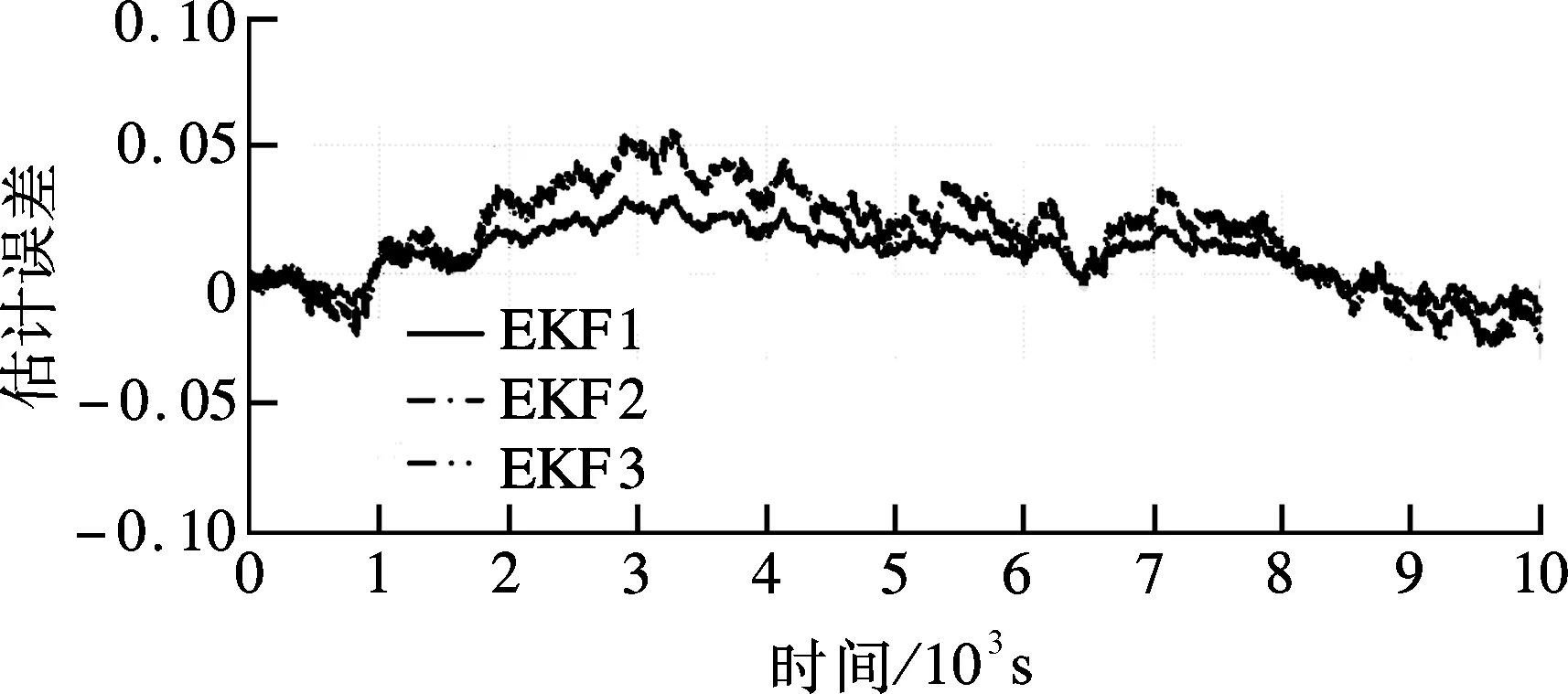
(b) SOC估计误差曲线

(a) SOC估计曲线与实际SOC曲线

(b) SOC估计误差曲线

(a) SOC估计曲线与实际SOC曲线

(b) SOC估计误差曲线

表5给出了不同温度下SOC估计值的最大误差.根据测试数据可见,引入环境变量后,电池模型更符合实际运行状况,SOC估算精度提高,间接地反映了所建立电池模型的合理性;引入温度补偿系数ηT后,低温下SOC估计精度有所提高．改进后的算法能够提高SOC估计精度．

表5 SOC估计最大误差 %

5 结论

1) 在锂电池的Thevenin模型中,将欧姆内阻、极化内阻、极化电容等参数定义为环境变量的函数,提高了电池模型的准确度,扩展了模型的适用范围．

2) 所采用的参数辨识方法考虑了锂电池的物理特性,测量结果准确,辨识得到的参数更加接近实际值．

3) 对锂电池状态方程进行改进,提高了滤波结果的精度,进一步提高了SOC估计结果的准确度．

实际电池使用过程中,所处环境温度是变化的,电池内部温度会随放电有一定的升高,在进一步的研究中,可以考虑采取变温度环境测试,验证该模型算法的合理性．

References)

[1]魏克新, 陈峭岩. 基于多模型自适应卡尔曼滤波器的电动汽车电池荷电状态估计[J]. 中国电机工程学报, 2012, 32(31): 19-26. DOI:10.13334/j.0258-8013.pcsee.2012.31.006. Wei Kexin, Chen Qiaoyan. Battery SOC estimation based on multi-model adaptive Kalman filter[J].ProceedingsoftheCSEE, 2012, 32(31): 19-26. DOI:10.13334/j.0258-8013.pcsee.2012.31.006.(in Chinese)

[2]周美兰, 王吉昌, 李艳萍. 优化的BP 神经网络在预测电动汽车SOC 上的应用[J]. 黑龙江大学自然科学学报, 2015, 12(1): 1-6. DOI:10.13482/j.issn1001-7011.2015.01.006. Zhou Meilan, Wang Jichang, Li Yanping. Optimized BP neural network in the prediction of electric vehicles SOC [J].JournalofNaturalScienceofHeilongjiangUniversity, 2015, 12(1): 1-6. DOI:10.13482/j.issn1001-7011.2015.01.006.(in Chinese)

[3]何耀, 张陈斌, 刘兴涛, 等. 基于信息融合的LiFePO4动力电池组SOC估计[J].控制与决策, 2014,29(1): 188-192. DOI:10.13195/j.kzyjc.2012.1441. He Yao, Zhang Chenbin, Liu Xingtao, et al. SOC estimation for LiFePO4high-power batteries based on information fusion[J].ControlandDecision, 2014, 29(1): 188-192. DOI:10.13195/j.kzyjc.2012.1441.(in Chinese)

[4]李司光, 张承宁. 锂离子电池荷电状态预测方法研究[J]. 北京理工大学学报, 2012, 32(2): 125-145. DOI:10.15918/j.tbit1001-0645.2012.02.023. Li Siguang, Zhang Chengning. State of charge evaluation of lithium-ion batteries[J].TransactionsofBeijingInstituteofTechnology, 2012, 32(2): 125-145. DOI:10.15918/j.tbit1001-0645.2012.02.023.(in Chinese)

[5]武国良, 周志宇, 于达仁. 应用非稳态开路电压方法估计EV用电池剩余电量研究[J]. 电机与控制学报, 2013, 17(4): 110-115. DOI:10.3969/j.issn.1007-449X.2013.04.018. Wu Guoliang, Zhou Zhiyu, Yu Daren. Unsteady open circuit voltage method for state of charge estimation of electric vehicle batteries[J].ElectricMachinesandControl, 2013, 17(4): 110-115. DOI:10.3969/j.issn.1007-449X.2013.04.018.(in Chinese)

[6]张云, 张承慧, 崔纳新. 锂离子电池荷电状态估计: 非线性观测器方法[J].控制理论与应用, 2012, 29(12): 1640-1644. Zhang Yun, Zhang Chenghui, Cui Naxin. Estimation of state-of-charge of lithium-ion battery: Nonlinear observer method[J].ControlTheory&Applications, 2012, 29(12): 1640-1644. (in Chinese)

[7]杨阳, 汤桃峰, 秦大同,等. 电动汽车锂电池PNGV等效电路模型与SOC 估算方法[J]. 系统仿真学报, 2012, 24 (4): 938-942. DOI:10.16182/j.cnki.joss.2012.04.019. Yang Yang, Tang Taofeng, Qin Datong, et al. PNGV equivalent circuit model and SOC estimation algorithm of lithium batteries for electric vehicle[J].JournalofSystemSimulation, 2012, 24(4): 938-942. DOI:10.16182/j.cnki.joss.2012.04.019.(in Chinese)

[8]贾玉健, 解大, 顾羽洁, 等. 电动汽车电池等效电路模型的分类和特点[J]. 电力与能源, 2011, 32(6): 516-521. Jia Yujian, Jie Da, Gu Yujie, et al. Classification and characteristics of circuit models for EV’s battery[J].PowerandEnergy, 2011, 32(6): 516-521. (in Chinese)

[9]Omar N, Widanage D, Abdel Monem M, et al. Optimization of an advanced battery model parameter minimization tool and development of a novel electrical model for lithium-ion batteries[J].InternationalTransactionsonElectricalEnergySystems, 2014, 24(12): 1747-1767. DOI:10.1002/etep.1815.

[10]戴海峰, 魏学哲, 孙泽昌. 基于等效电路的内阻自适应锂离子电池模型[J]. 同济大学学报(自然科学版), 2010, 38(1): 98-102.DOI:10.3969/j.issn.0253-374x.2010.01.018. Dai Haifeng, Wei Xuezhe, Sun Zechang. An inner resistance adaptive model based on equivalent circuit of lithium-ion batteries[J].JournalofTongjiUniversity(NaturalScience), 2010, 38(1): 98-102.DOI:10.3969/j.issn.0253-374x.2010.01.018. (in Chinese)

[11]Jang J, Yoo J. Equivalent circuit evaluation method of lithium polymer battery using bode plot and numerical analysis[J].IEEETransactionsonEnergyConversion, 2011, 26(1): 290-298. DOI:10.1109/tec.2010.2089796.

[12]Unterrieder C, Priewasser R, Agostinelli M, et al. Comparative study and improvement of battery open-circuit voltage estimation methods [C]//IEEE55thInternationalMidwestSymposiumonCircuitsandSystems. Boise, Idaho, USA, 2012: 1076-1079. DOI:10.1109/MWSCAS.2012.6292210.

[13]Xiong R, He H W, Zhao K. Research on an online identification algorithm for a thevenin battery model by an experimental approach[J].InternationalJournalofGreenEnergy, 2015,12(3): 272-278. DOI:10.1080/15435075.2014.891512.

[14]Pathuri B V, Christoph U, Mario H. Battery internal state estimation: A comparative study of non-linear state estimation algorithms[C]//9thIEEEVehiclePowerandPropulsionConference. Beijing, China, 2013: 15-18. DOI: 10.1109/VPPC.2013.6671666.

[15]李哲, 韩雪冰, 卢兰光，等. 动力型磷酸铁锂电池的温度特性[J]. 机械工程学报, 2011, 47(18): 115-120.DOI:10.3901/JME.2011.18.115. Li Zhe, Han Xuebing, Lu Languang,et al. Temperature characteristics of power LiFePO4batteries[J].JournalofMechanicalEngineering, 2011, 47(18): 115-120. DOI:10.3901/JME.2011.18.115.(in Chinese)

[16]Liu Y Y, He Z W, Gao M Y, et al. Dual estimation of lithium-ion battery internal resistance and SOC based on the EKF[C]//IEEE5thInternationalCongressonImageandSignalProcessing. Chongqing, China,2012:1639-1643. DOI:10.1109/cisp.2012.6469649.

[17]Plett G L. Extended Kalman filtering for battery management systems of LiPB2based HEV battery packs[J].JournalofPowerSources, 2004, 134(2): 277-292. DOI:10.1016/j.jpowsour.2004.02.033.

[18]全国汽车标准化技术委员会. QC/T743—2006 电动汽车用锂离子蓄电池[S]. 北京: 中国标准出版社, 2006.

[19]刘新天, 刘兴涛, 何耀, 等. 基于Vmin-EKF的动力电池组SOC估计[J]. 控制与决策, 2010, 25(3): 445-449. DOI:10.13195/j.cd.2010.03.128.liuxt.006. Liu Xintian, Liu Xingtao, He Yao, et al. Based-Vmin-EKF SOC estimation for power Li-ion battery pack[J].ControlandDecision, 2010, 25(3): 445-449. DOI:10.13195/j.cd.2010.03.128.liuxt.006. (in Chinese)

[20]He H W, Qin H Z, Sun X K, et al. Comparison study on the battery SoC estimation with EKF and UKF algorithms[J].Energies, 2013, 6(10): 5088-5100. DOI:10.3390/en6105088.

[21]Kim J, Cho B H. State-of-charge estimation and state-of-health prediction of a Li-ion degraded battery based on an EKF combined with a per-unit system[J].IEEETransactionsonVehicularTechnology, 2011, 60(9): 4249-4260. DOI:10.1109/tvt.2011.2168987.

SOC estimation method based on lithium-ion cell model considering environmental factors

Liu Xintian Sun Zhangchi He Yao Zheng Xinxin Zeng Guojian

(Clean Energy Automotive Research Institute, Hefei University of Technology, Hefei 230009, China)

The internal parameters of the cell at different temperatures and state-of-charge (SOC) were tested and calculated. The factors affecting the variations of parameters were analyzed. The Thevenin model of the lithium-ion cell with variable parameters was established. The gist of segmentation and the method for determining the correlation parameters of the model were discussed. The extended Kalman filter (EKF) algorithm was used to estimate SOC. An improved SOC estimation method which is based on the temperature was given. The proposed cell model can avoid the application limitation of the existing models without considering the influences of environmental factors. Simulation and experimental results show that the SOC estimation method based on the established model can achieve higher accuracy in a wide temperature range.

power li-ion cell; state-of-charge; temperature compensation; Thevenin model; extended Kalman filter

10.3969/j.issn.1001-0505.2017.02.018

2016-06-05. 作者简介:刘新天(1981—)，男，博士,副研究员，xintian.liu@hfut.edu.cn.

国家自然科学基金资助项目(21373074)、安徽省国际科技合作计划资助项目(1303063010).

刘新天，孙张驰,何耀，等.基于环境变量建模的锂电池SOC估计方法[J].东南大学学报(自然科学版),2017,47(2):306-312.

10.3969/j.issn.1001-0505.2017.02.018.

TM912

A

1001-0505(2017)02-0306-07