8自由度铺丝机械手的自运动流形分析
徐 朋 赵东标 应明峰 程锦翔 李 奎
(南京航空航天大学机电学院, 南京 210016)
8自由度铺丝机械手的自运动流形分析
徐 朋 赵东标 应明峰 程锦翔 李 奎
(南京航空航天大学机电学院, 南京 210016)
针对梯度投影算法所得冗余机械手关节逆解不一定包括最优解的缺陷,提出一种分析8自由度冗余铺丝机械手关节逆解的流形方法. 利用流形法所得逆解包含了冗余机械手的全部关节逆解,有利于实现自运动控制的全面优化.根据逆解流形的空间多维特性,在8自由度铺丝机械手的关节空间内分别定义其位置关节子流形和姿态关节子流形,并分别得到三维空间中仿真映射曲面.结果表明,由于芯模自由度是在固定空间内的运动,相比于7自由度的铺丝机械手,8自由度铺丝机械手的仿真曲面流形在灵活性及避障碍能力方面均有较大提高.最后以飞机S形进气道为例进行仿真,仿真结果表明,仿真轨迹与期望轨迹高度吻合,证明了所提方法的正确性.
流形;铺丝;逆解;进气道
复合材料纤维铺放成型技术[1-2](fiber placement technology)是一种复合材料成型技术,在航空航天制造中拥有重要地位.随着航空工业的发展,高强度、轻质量的复合材料需求量进一步加大,纤维铺放成型技术逐渐成为了研究的热点.因此针对复合材料纤维铺放工艺技术的成型装备[3-4]——铺丝机械手的研究已经成为当今先进制造技术研究中的一个新方向.
铺丝机械手一般都是冗余机械手[5],冗余机械手的逆运动学解具有自运动流形的结构[6],自运动流形在空间反映了机械手的全部关节构型.(2)Moll等[7]通过在关节空间寻找流形上的最小能量曲线方法,实现了末端运动轨迹的最优化.Burdick[8]给出位置空间3R机构和4R机构的流形分析,并得出解流形的切空间同构于Jacobian矩阵零空间的结论.Galicki[9]利用反自由控制算法详细分析了冗余机械手的关节空间流形,得出逆解流形的最小和最大取值区间.赵建文等[10]得到了特殊结构冗余机器人参数化的自运动流形,但没有具体给出解空间和工作空间之间的流形映射关系.葛新锋等[11]利用位姿分离方法分析了冗余铺丝机械手关节逆解流形,7自由度铺丝机械手只有一个冗余自由度,其在铺丝工作过程中的灵活性及避障碍能力有一定局限性,不利于自运动控制的选择.
因此,本文提出一种位置和姿态相耦合的8自由度铺丝机械手模型.不仅增强了铺丝机械手在整个工作过程中的灵活性及避障碍能力,而且有利于后续自运动控制的优化选择.8自由度铺丝机械手关节空间拥有无数多个逆解,所有逆解一起构成多维空间中的解流形.
1 8自由度铺丝机械手模型
图1为8自由度铺丝机械手模型.由单自由度芯模、6自由度库卡机械手及单自由度滑动导轨组成. 相对于7自由度位姿分离式铺丝机械手, 8自由度铺丝机械手模型各个关节之间存在强耦合关系,可以适应更复杂的工作环境及有助于逆解和自运动控制的进一步优化.

图1 8自由度铺丝机械手模型
2 8自由度铺丝机械手关节逆解
本文基于旋量理论[12-13]通过设定双冗余变量,计算分析8自由度铺丝机械手的关节逆解,各连杆间的尺寸参数及初始运动状态如图2所示.图中,a1~a6分别为机械手的尺寸参数;d1为冗余关节变量值;r1~r5为各自轴线上的点;ξ1~ξ8为相应的单位运动旋量.
初始运动状态下惯性坐标系xsyszs与工具坐标系xtytzt之间的齐次变换为
(1)
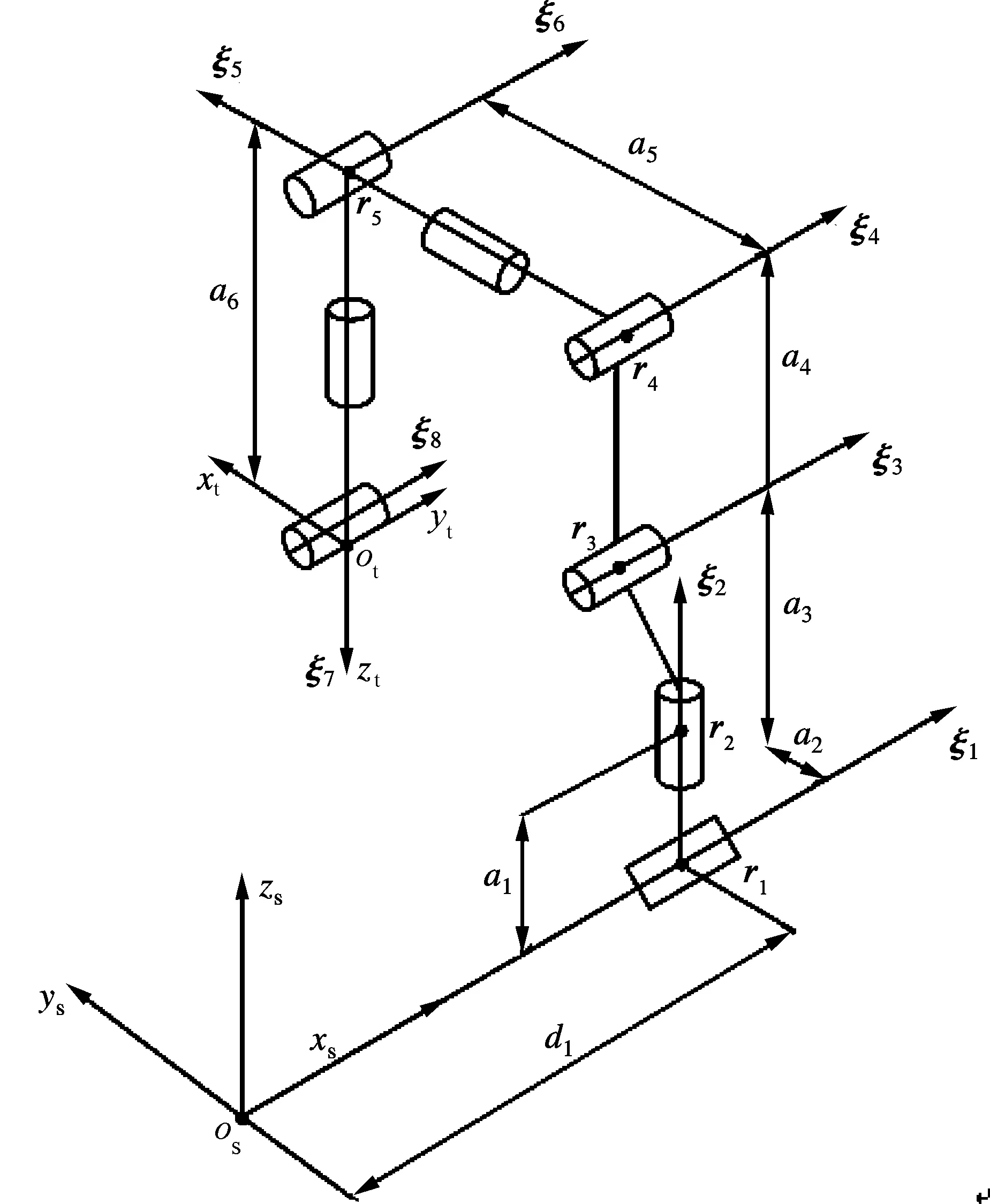
图2 冗余铺丝机械手初始运动状态
一般工作状态下惯性坐标系与工具坐标系之间的齐次变换为
(2)
式中,θ8为芯模旋转角度;α为旋转芯模轴线与铺丝头压辊轴线之间的夹角;r为铺丝运动轨迹点处的切线半径.
将d1和θ8分别设定为冗余变量,根据旋量理论及各已知旋量子问题,可得
θ2=arctan2(∓(qx-d1),±qy)
(3)
(4)
(5)
(6)
(7)
θ7=arctan2((d1-q″x),(a2+a5-q″y))
(8)
(9)
(10)
(11)
(12)
(13)
式(3)~(8)中,当冗余关节d1,θ8在固定范围内变化时,本文计算所得关节逆解θ2,θ3,θ4,θ5,θ6,θ7均是以d1,θ8为变量的函数.为了实际铺丝工作中方便测量和计算,本文以d1,θ8作为冗余关节来计算逆解及流形分析,其中θ8包含于gst(θ).
3 仿真验证
定义关节构型空间为
C=C1C2C3C4C5C6C7C8
(14)
式中,C1为移动关节构型空间;C2~C7为6自由度机械手各关节构型空间;C8为芯模转角构型空间.
定义位置关节构型空间为
Cwz=C1C2C3C4C8
(15)
定义位置关节工作空间流形为
(Cwl,Fwl)={(θwl,fwl(θwl))/fwl(θwl)=
low,θwl∈Cwz}
(16)
式中,low为从惯性坐标系原点到机械手腕点的位置矢量;θwl={d1,θ2,θ3,θ4,θ8}T;Cwl为位置关节工作空间流形.
定义姿态关节构型空间为
Czt=C2C3C4C5C6C7C8
(17)
定义姿态关节工作空间流形为
(Czl,Fzl)= {(θzl,fzl)/fzl(θzl)=
(low,xt,zt),θzl∈Czt}
(18)
式中,xt,zt为工具坐标系的姿态矢量;θzl={θ2,θ3,θ4,θ5,θ6,θ7,θ8}T;Czl为姿态工作空间流形.
8自由度铺丝机械手本体结构参数定义如下:
(19)
(20)

(a) 右上臂形
(b) 右下臂形

(c) 左上臂形
(d) 左下臂形
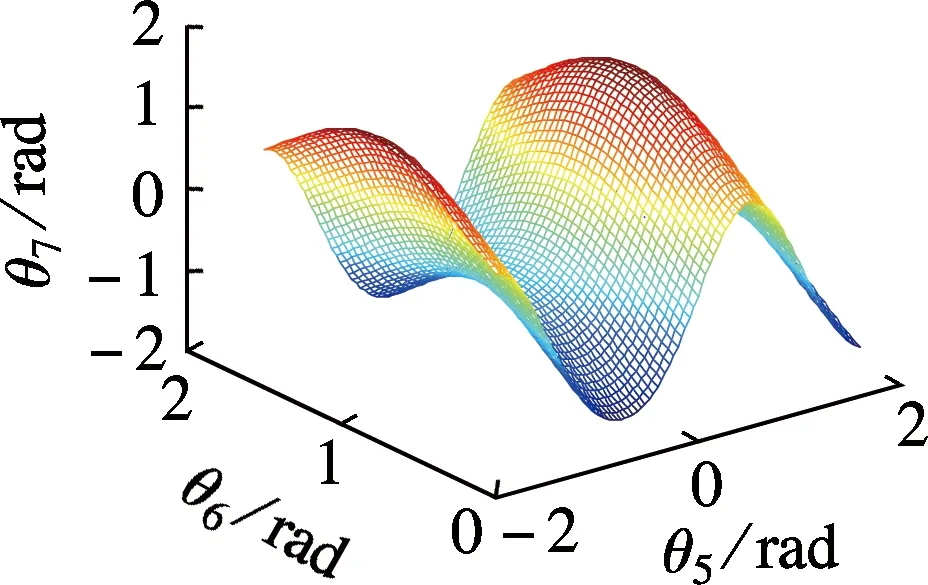
由于在实际工作过程中铺丝机械手一般处于左上臂形和右上臂形2种情形.本文在铺丝机械手正常工作过程中针对芯模铺丝轨迹,在位置关节空间和姿态关节空间作了相应的自运动流形仿真.其中式(16)展示的关节位置空间是五维的自运动流形,受空间维数的限制,本文仅将位置流形映射到θ2,θ3,θ4组成的位置关节空间(见图4),将式(18)展示的七维姿态流形映射到θ5,θ6,θ7组成的腕关节空间(见图5和6).

(a) 左上臂形

(b) 右上臂形
(a) 翻腕

(b) 不翻腕
鉴于铺丝机械手关节空间存在自运动特性,所以也可以将姿态空间流形和位置空间流形分别映射到其他关节定义的三维空间.这样得到的自运动流形是不同的,但是不同自运动流形之间的关节运动构型是一致的.
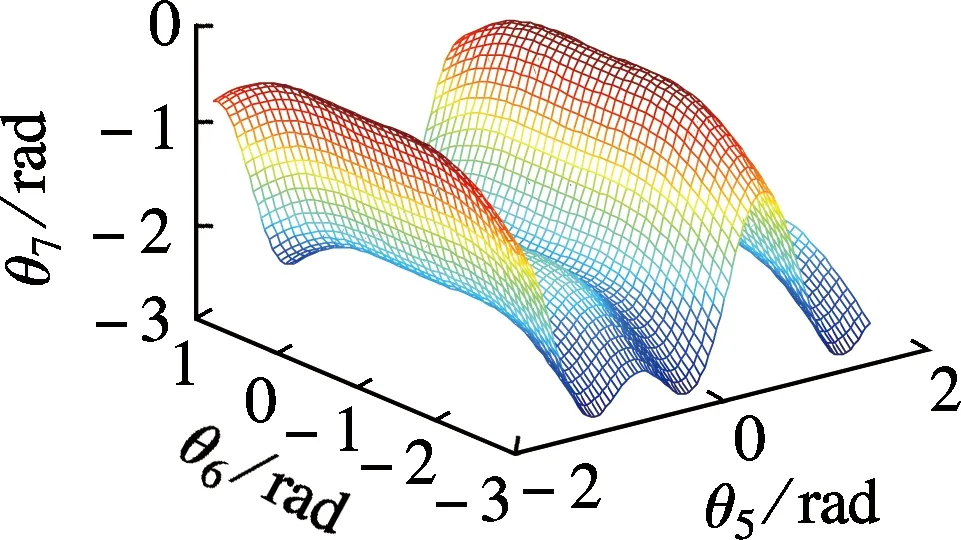
(a) 翻腕
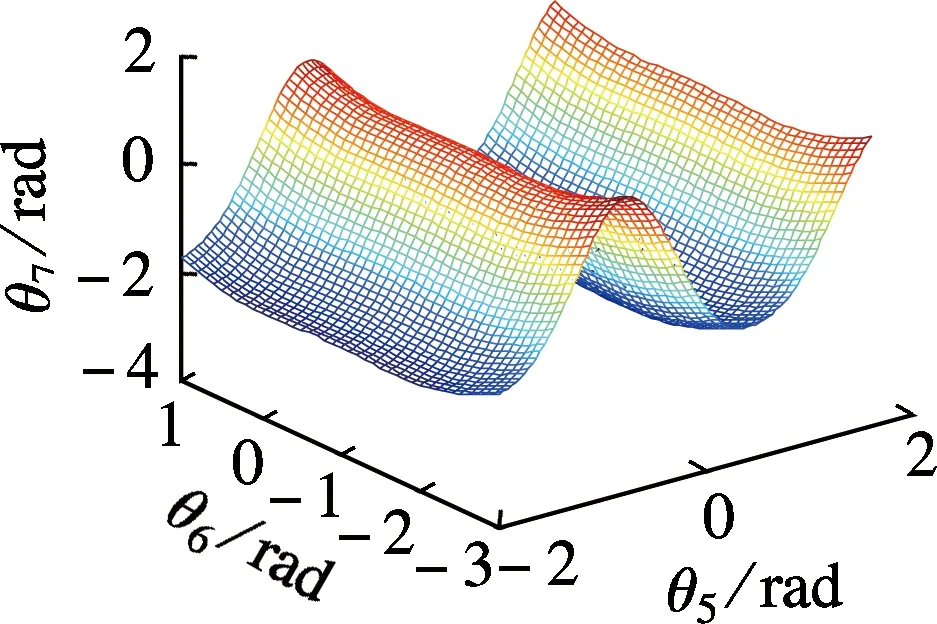
(b) 不翻腕
对于7自由度铺丝机械手,以位置关节为例得出其在右上臂形和左上臂形标志下的仿真流形,图7分别为空间中的曲线流形.由于芯模自由度是在固定空间内的运动,因此当芯模上的铺丝轨迹点运动完全确定时,芯模自由度就会被约束.这样7自由度铺丝机械手就会失去冗余特性,其逆运动学解将是空间中的有限离散点,灵活性和避障碍能力将会变差,也不利于后续最优自运动控制的实现,而8自由度铺丝机械手可以很好地解决这一问题.
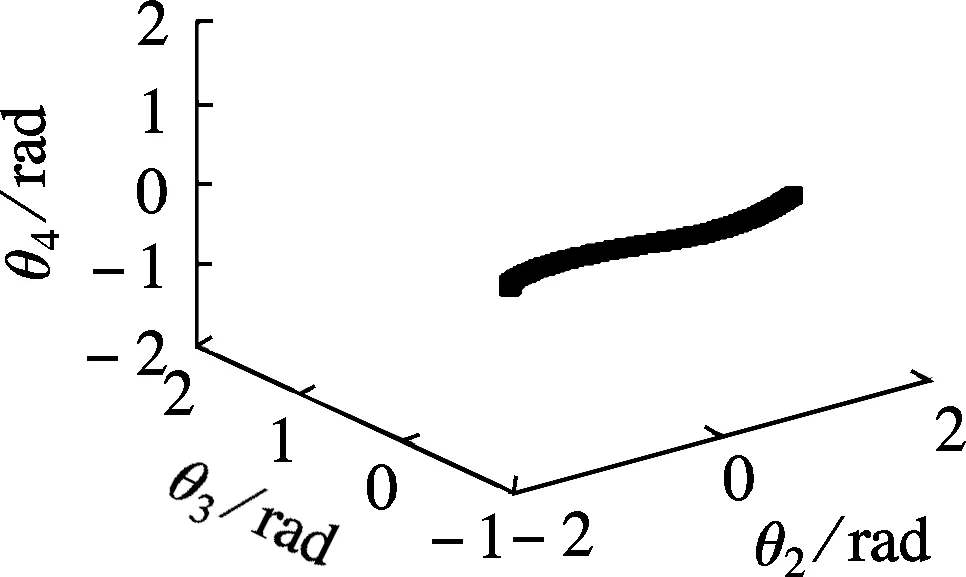
(a) 左上臂形

(b) 右上臂形
下面通过飞机S形进气道铺丝轨迹点为例来验证本文所得逆解流形的正确性.

图8 飞机S形进气道仿真轨迹
由图8可见,期望轨迹和仿真轨迹高度吻合,由此证明了本文所用自运动流形法的正确性.
4 结语
利用自运动流形方法得到了8自由度铺丝机械手的全部关节逆解,由于流形中肯定含有最优逆解,所以有效避免了梯度投影算法所得逆解不一定是最优逆解的缺陷,为后续的自运动最优控制奠定了基础.根据关节逆解的自运动流形特点,可以利用微分流形理论在曲面上研究铺丝机械手的逆解,最后通过飞机S形进气道验证了本文所得结论的正确性.
References)
[1]Bruyneel M, Zein S. A modified fast marching method for defining fiber placement trajectories over meshes[J].ComputersandStructures, 2013, 125: 45-52. DOI:10.1016/j.compstruc.2013.04.015.
[2]方宜武, 王显峰, 顾善群, 等. 自动铺丝过程中预浸料的侧向弯曲[J]. 材料工程, 2015, 43(4): 47-52.DOI:10.11868/j.issn.1001-4381.2015.04.009. Fang Yiwu, Wang Xianfeng, Gu Shanqun, et al. Lateral bending of prepreg during automated fiber placement[J].JournalofMaterialsEngineering, 2015, 43(4): 47-52.DOI:10.11868/j.issn.1001-4381.2015.04.009.(in Chinese)
[3]段玉岗, 董肖伟, 葛衍明, 等. 基于CATIA生成数控加工路径的机器人纤维铺放轨迹规划[J]. 航空学报, 2014, 35(9): 2632-2640 DOI:10.7527/S1000-6893.2013.0471. Duan Yugang, Dong Xiaowei, Ge Yanming, et al. Robotic fiber placement trajectory planning based on CATIA CNC machining path[J].ActaAeronauticaetAstronauticaSinica, 2014, 35(9): 2632-2640. DOI:10.7527/S1000-6893.2013.0471. (in Chinese)
[4]Schmidt C, Schultz C, Weber P, et al. Evaluation of eddy current testing for quality assurance and process monitoring of automated fiber placement[J].CompositesPartB:Engineering, 2014, 56(17): 109-116. DOI:10.1016/j.compositesb.2013.08.061.
[5]郭迪, 孙富春, 刘华平, 等. 基于Kinect的冗余机械臂直线推移操作控制[J]. 东南大学学报(自然科学版), 2013, 43(I): 143-147. DOI:10.3969/j.issn.1001-0505.2013.S1.030. Guo Di, Sun Fuchun, Liu Huaping, et al. Line pushing control of redundant manipulator based on Kinnect[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2013, 43(Ⅰ): 143-147.DOI:10.3969/j.issn.1001-0505.2013.S1.030.(in Chinese)
[6]An H H, Clement W I, Reed B. Analytical inverse kinematic solution with self-motion constraint for the 7-DOF restore robot arm[C]//2014IEEE/ASMEInterna-tionalConferenceonAdvancedIntelligentMechatronics. Besancon, France, 2014: 1325-1330. DOI:10.1109/aim.2014.6878266.
[7]Moll M, Kavraki L E. Path planning for minimal energy curves of constant length[C]//Proceedingsofthe20 04IEEEInternationalConferenceonRoboticsandAuto-mation. New Orleans, USA, 2004: 2826-2831. DOI:10.1109/robot.2004.1307489.
[8]Burdick J W. On the inverse kinematics of redundant manipulators: Characterization of the self-motion mani-folds[C]//Proceedingsofthe1989IEEEInternationalConferenceonRoboticsandAutomation. Scottsdale, USA, 1989: 264-270. DOI:10.1109/robot.1989.99999.
[9]Galicki M. Inverse-free control of a robotic manipulator in a task space[J].RoboticsandAutonomousSystems, 2014, 62(2): 131-141. DOI:10.1016/j.robot.2013.11.005.
[10]赵建文, 杜志江, 孙立宁. 7自由度冗余手臂的自运动流形[J]. 机械工程学报, 2007, 43(9): 132-137.DOI:10.3321/j.issn:0577-6686.2007.09.027. Zhao Jianwen, Du Zhijiang, Sun Lining. Self-motion manifolds of a 7-DOF redundant manipulator[J].JournalofMechanicalEngineering, 2007, 43(9): 132-137.DOI:10.3321/j.issn:0577-6686.2007.09.027.(in Chinese)
[11]葛新锋, 赵东标. 7自由度自动铺丝机器人参数化的自运动流形[J]. 机械工程学报, 2012, 48(13): 27-31. DOI:10.3901/JME.2012.13.027. Ge Xinfeng, Zhao Dongbiao. Parameterized self-motion manifold of 7-DOF automatic fiber placement robotic manipulator[J].JournalofMechanicalEngineering, 2012, 48(13): 27-31. DOI:10.3901/JME.2012.13.027. (in Chinese)
[12]戴建生. 机构学与旋量理论的历史渊源以及有限位移旋量的发展[J]. 机械工程学报, 2015, 51(13): 13-26. DOI:10.3901/JME.2015.13.013. Ddi Jiansheng. Historical relation between mechanisms and screw theory and the development of finite displace-ment screws[J].JournalofMechanicalEngineering, 2015, 51(13): 13-26.DOI:10.3901/JME.2015.13.013.(in Chinese)
[13]Zheng F Y, Hua L, Han X H. The mathematical model and mechanical properties of variable center distance gears based on screw theory[J].MechanismandMachineTheory, 2016, 101: 116-139. DOI:10.1016/j.mechmachtheory.2016.03.005.
Self-motion manifold analysis on 8-DOF fiber placement manipulator
Xu Peng Zhao Dongbiao Ying Mingfeng Cheng Jinxiang Li Kui
(College of Mechanical & Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)
In consideration of the disadvantage that the inverse solutions of redundant manipulator’sjoints based on the gradient projection method were not always optimal, a new method using manifolds to analyze the inverse solutions of an 8-DOF fiber placement manipulator’s joints was proposed in this study. The self-motion manifolds obtained by this method contain all of the inverse kinematic solution of fiber placement manipulator that helps to optimize the self-motion control roundly. According to the multi-dimensional characteristics of self-motion manifolds, the position joints space sub-manifolds and posture joints space sub-manifolds were respectively defined in working space of the 8-DOF fiber placement manipulator joint space, and the corresponding triaxial simulation curves of the manifolds were obtained respectively. The results show that the 8-DOF fiber placement manipulator, compared with the 7-DOF fiber placement manipulator, improved a lot in its flexibility and obstacle avoidance abilities because the motion corresponding to the mandrel’s degree of freedom was in the fixed space. In the last, the method was verified by using the S-shaped inlet simulation. The result shows that the simulation trajectory was highly consistent with the desired trajectory which proved validity of the method proposed by the paper.
manifolds; fiber placement; inverse solutions; inlet
10.3969/j.issn.1001-0505.2017.02.010
2016-08-21. 作者简介: 徐朋(1982—),男,博士生;赵东标(联系人),男,博士,教授,博士生导师,zdbme@nuaa.edu.cn.
国家自然科学基金资助项目(51175261)、国家重点基础研究发展计划(973计划)资助项目(2014CB046501)、高等学校博士学科点专项科研基金资助项目(20123218110020).
徐朋,赵东标,应明峰,等.8自由度铺丝机械手的自运动流形分析[J].东南大学学报(自然科学版),2017,47(2):254-258.
10.3969/j.issn.1001-0505.2017.02.010.
TP242.2
A
1001-0505(2017)02-0254-05

