水平荷载下地下连续墙—桩组合基础数值分析

刘聪，魏焕卫*，张伟，杨庆义

（1.山东建筑大学土木工程学院，山东济南250014；2.山东电力工程咨询院，山东济南250013）

水平荷载下地下连续墙—桩组合基础数值分析

刘聪1，魏焕卫1*，张伟2，杨庆义2

（1.山东建筑大学土木工程学院，山东济南250014；2.山东电力工程咨询院，山东济南250013）

鉴于地下连续墙用材量较大的缺陷，研究一种新型基础形式——地下连续墙与桩组合基础，为地下连续墙新技术的发展提供理论依据。文章针对水平荷载作用下地下连续墙-桩组合基础的水平承载性状，采用有限差分软件FLAC3D进行数值模拟分析，通过数值计算测点的位移、弯矩曲线研究，分析了组合基础在不同水平荷载、不同长度比、有无竖向荷载、土体弹性模量、内摩擦角、粘聚力等因素影响下的水平变形及内力变化规律。结果表明：荷载等级和墙桩长度比对组合基础的水平变形和内力变化影响敏感度较为突出，地下连续墙与桩的长度比为4∶6时设计更合理；组合基础顶部以下1/2的部分是承担大部分水平变形和内力变化的位置，新型组合基础的受力特性符合了变刚度设计新理念，即变形大的位置增加刚度，减小变形，而变形小的地方则减小刚度，节省费用；新型组合基础上部和地下连续墙与桩的连接处存在两个最不利影响作用部位，需要着重考虑最不利影响问题。

地下连续墙—桩组合基础；水平荷载；数值模拟

0 引言

随着工程水平的日益提高，地下基础形式向大规模、大深度方向发展的进程中，也遇到越来越多的问题。如发电厂建筑尤其是主厂房及锅炉等，因其工艺的特殊性，结构往往承受很大的水平何载，并且水平荷载成为其主要的控制荷载［1］。目前，抵抗水平力的结构构件主要有基础、桩、地下连续墙，其中水平受荷桩应用最为广泛。随着建筑基础承受较大水平力的情况越来越多，对桩的水平承载力提出更大的要求，常规提高桩的水平承载力的方法作用越来越有限；为此，作为抵抗水平荷载主要构件的地下连续墙以其自身整体刚度大、安全性好等优点逐步替代了桩基础、沉箱基础或沉井［2］，来承担更大的荷载，使得承载性能优越的地下连续墙得到了迅猛发展。地下连续墙有一个明显的缺点即用材量较大。从材料使用角度来看，选用基础时地下连续墙并没有优势。从绿色经济的设计理念出发，研究一种新型基础——地下连续墙与桩组合基础。

在研究方法和理论研究方面，基于地下连续墙技术的不断进步，日本最先将桩基与地下连续墙结合，形成了一系列的组合基础，地下连续墙与桩基协同工作，但大都用于承担上部荷载（如用于既有建筑物的抗震抗液化基础）［3-4］。戴国亮等对闭合式地下连续墙基础的水平承载特性进行了深入的探究［5］；郭河等对组合荷载作用下井筒式地下连续墙的水平承载机理进行了数值模拟［6］；宋章通过分析闭合墙基础的水平受力变形分布规律，得出了水平荷载下闭合墙基础呈整体倾斜破坏特征［7］；魏焕卫等对水平受荷桩的变形和受力规律进行研究［8-9］；费利娅等通过电厂桩基工程在非饱和黄土地层中水平荷载试验，得出桩—土共同作用时灌注桩的变形规律［10］；陈晓东等提出闭合型地下连续墙在水平荷载作用下的两种工作状态和作用机理［11］；张瑞棋等提出了在水平荷载作用下地下连续墙对周围土体的挤压作用规律［12］。虽然国内外学者分别对地下连续墙和桩基础做了大量的实验和数值模拟分析等，但是对于地下连续墙与桩这种新型组合基础却涉及很少。地下连续墙与桩组合基础的工作机理极为复杂，在水平载荷方面，所做研究大多局限于对水平承载力的研究，没有对水平承载性状和机理作进一步的探讨。对地下连续墙与桩组合基础的受力机理、承载能力、节点连接、施工工艺等方面尚未进行深入系统的研究，目前缺乏地下连续墙与桩组合设计施工的理论依据，其设计施工主要依靠自身的经验，而无法依据共同作用机理进行设计及施工。针对水平荷载对建筑物基础影响的研究，文章通过FLAC3D软件进行数值模拟，着重探究有限差分模型所涉及参数的改变对地下连续墙与桩组合基础的水平变形和内力变化的影响。

1 数值模型的建立

1.1 模型建立的基本原理

地下连续墙与桩组合基础承受水平方向的荷载，实质上就是地下连续墙与桩组合基础和土的相互作用。采用FLAC3D软件对构件的结构内力和变形进行分析，把地下连续墙与桩的组合基础作为刚性的接触单元，而把地下连续墙与桩组合基础的周围土体作为柔性的接触单元，从而形成接触对。为了能够真实合理的模拟组合基础与土体的相互之间的作用，可以通过设定法向接触的刚度因子、剪切向接触的刚度因子、摩擦角以及粘聚力来真实地控制接触面单元之间接触的行为，并且允许地下连续墙与桩组合基础与周围土体可以相对的滑动但是不会允许其相互分离。

1.2 模型基本假设

模型在计算中所遵循的基本假设：

（1）模型选用的土为均质、连续且各向同性的理想弹塑性材料，选取的本构模型为摩尔库伦本构模型；

（2）组合基础材料看作各向同性的弹性材料，本构模型选取的是弹性本构模型；

（3）组合基础与周围土体可以相对的滑动但是不会允许其相互分离，也就是处于接触但滑动状态；

（4）考虑到在施工之前地下连续墙与桩组合基础周围的土体已经完成了固结或者说接近于固结，由此因自重所产生的初始的位移场必须消除，但是因自重产生的应力场必须保留；

（5）不考虑地下水的影响。

1.3 模型的尺寸与边界条件

组合基础模型（如图1所示）上部地下连续墙选取的形式是闭合“回”字形其水平方向上的长度为5 m、宽度为3 m、竖直方向上的高度为3 m、墙厚为1 m；组合基础下部桩长为7 m，采用的是直径为0.8 m混凝土桩，采用上下串联方式，连接部分采用刚接。为了避免边界效应的影响，模型周围土体尺寸取3倍模型的尺寸。根据实际工程中的受力情况和周围土体对其组合基础的影响效果等因素，模型的边界条件为组合基础及周围土体顶部自由，模型底部采用两个方向的固定边界，模型两侧采用水平方向的固定边界。由于侧重考虑组合基础受水平荷载的情况，因此加载方式采用在地下连续墙长边方向的顶部施加线荷载。

图1 组合基础模型图

1.4 模型的计算参数

地下连续墙、桩和周围土体均采用8个节点的实体六面体单元单元进行模拟，模型包括392124网格节点和115992个单元。实体单元能很好的满足模拟实验的弹性以及理想弹塑性的要求，依据弹性理论和勘察报告中给出的压缩模量，定义模型的计算参数见表1、2。

表1 土体的物理力学参数

表2 地下连续墙与桩组合基础的物理力学参数

2 数值模拟影响因素分析

通过FLAC3D软件后处理提取测点的位移和应力，绘制位移和弯矩曲线，在此基础上主要探索了组合基础在不同等级的水平荷载、不同墙桩长度比、有无竖向荷载，土体弹性模量、内摩擦角、粘聚力等影响因素下水平变形及内力变化规律。

2.1 不同的水平荷载对组合基础水平变形和内力的影响

在水平荷载的作用下，组合基础的受力性状极为复杂，其中涉及到桩组合基础和组合基础的内芯土、周围土体之间的相互作用，以及组合基础地下连续墙与桩刚接处受土面积突变等原因。水平承载能力不仅跟组合基础的整体刚度、材料强度有关，同时也很大程度上取决于组合基础内部土体与周围土体的横向抗力。在水平荷载作用下，组合基础克服自身材料强度产生挠曲变形，随着挠曲变形的作用，土体受到挤压而产生抗力，这一抗力将阻止组合基础挠曲变形的进一步发展，从而构成了复杂的相互作用体系［13］。

考虑不同水平荷载条件下对组合基础的变形和弯距进行计算分析。由图2（a）可知，组合基础的水平变形绝大部分发生在上部地下连续墙处；不同水平荷载作用下，反弯点的位置受水平荷载的影响较小；随着入土深度的增加，组合基础的水平变形规律和梁板的挠曲变形十分相似。组合基础的侧向变形随深度逐渐趋于定值，说明下部桩对于控制水平变形所起到的作用很小，所以对组合基础下部桩的参数设计时可以考虑选取合理桩长。

由图2（b）可知，组合基础的弯矩随着入土深度的增加，呈先减小后增大的趋势，在组合基础地下连续墙与桩的连接部位达到弯矩的最大值，最后随深度逐渐趋于定值零；弯矩变化是呈非线性变化；随着荷载的增加，弯矩值也相应的表现出变大的趋势。不同的水平荷载影响下水平位移与水平荷载的关系曲线图如图3所示。由图3可以看出，随着水平荷载的增加，组合基础水平位移与水平荷载的关系曲线呈非线性，表明上部土体出现塑性区。

不同的水平荷载影响下组合基础的水平变形和弯矩曲线形成的原因是组合基础随着入土深度的增加，土对组合基础的反向作用力也逐步增加，土对组合基础的反向作用力很好的抵消部分组合基础的水平推力；此外组合基础在水平力、侧摩阻力以及组合

图2 不同的水平荷载影响下组合基础的水平变形和弯矩图

基础内外土芯挤压共同作用下形成了非常复杂的受力体系。地下连续墙与桩刚接处反向弯矩达到最大值，是由于两者受土面积存在很大差异以及两者的刚度突变等因素造成的；组合基础下半部分的弯矩和位移趋于零，则是由于水平力对组合基础的作用效果随着入土深度的增加逐渐消散，上部荷载没有传递到底部的原因。因此在实际工程中可以增加上部的配筋率的同时减小下部的配筋率［9］。

2.2 不同长度比对组合基础水平变形和内力的影响

考虑地下连续墙与桩在不同墙桩长度比条件下对组合基础的水平变形和弯距的影响，计算结果如图4所示。

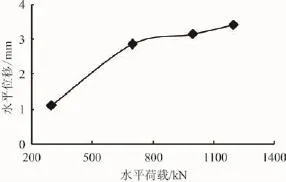
图3 不同的水平荷载影响下水平位移与水平荷载的关系曲线图

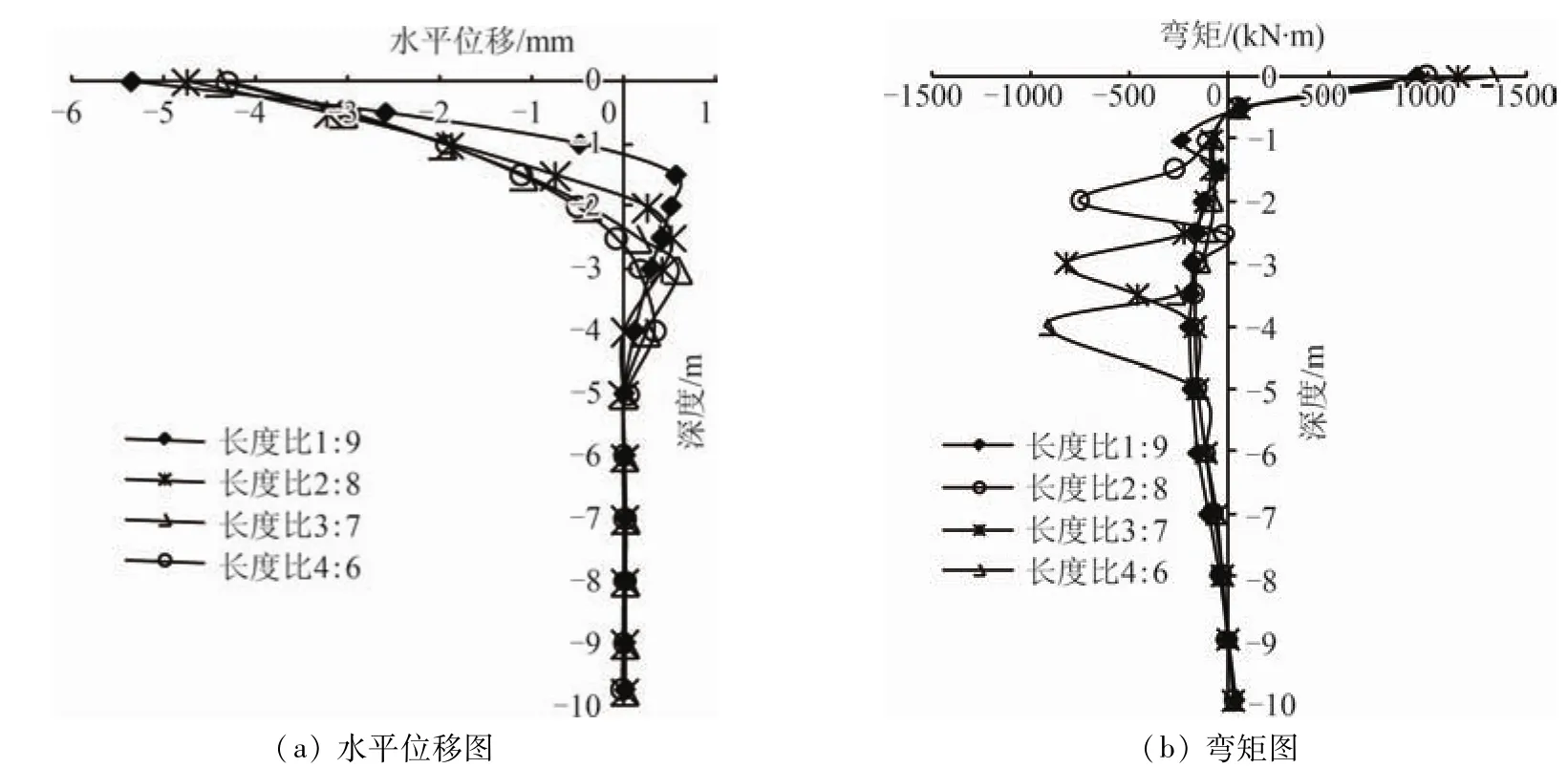
图4 不同长度比影响下组合基础的水平变形和弯矩图

由图4（a）可知，水平荷载作用下，组合基础的水平变形主要发生在上部，说明组合基础的上部是承担水平荷载的主要部分；四种不同长度比条件下，组合基础水平位移的分布趋势十分相似；随着地下连续墙与桩长度比的增大，反方向位移的最大值相应地减小，同时反弯点的位置逐渐降低，在长度比3∶7和长度比4∶6的两种情况下反弯点相对趋于稳定；不同墙桩长度比的组合基础反向位移最大值点存在差异，按照不同的组合方式共分为：墙桩比1∶9的组合基础反向位移最大值点位于-1 m附近；墙桩比2∶8的组合基础反向位移最大值点位于-2 m附近；墙桩比3∶7的组合基础反向位移最大值点位于-3 m附近；墙桩比4∶6的组合基础反向位移最大值点位于-4 m附近。即不同墙桩长度比的组合基础反向最大位移点位于地下连续墙与桩刚接的部位附近，即由于刚度突变原因此处存在最不利影响作用，由此可知在实际工程中，地下连续墙与桩刚接处是工程设计需要特别关注的部位。

图4（b）是不同长度比对组合基础内力的影响，随着墙桩长度比由小变大，组合基础负弯矩最大值逐渐增大，说明随着地下连续墙所占比重的增加，组合基础的水平抗弯能力有了明显提高，这是由于地下连续墙所占比重增加导致组合基础整体刚度提高，进而提高了组合基础的水平抗弯能力；但是随着长度比逐渐变大，负弯矩最大值的增长趋势逐渐变缓，最后负弯矩最大值趋于稳定，因此在实际工程中对组合基础要选取合理的墙桩长度比，避免造成材料得不到充分利用，产生浪费。由图5可以看出组合基础水平位移与不同长度比呈非线性关系，墙桩长度比不同，地下连续墙与桩对水平荷载的分担比不同。

不同长度比影响下组合基础的水平变形和弯矩曲线形成的原因：水平荷载通过组合基础上部的地下连续墙传递到深层土中，随着长度比的不断增加，水平荷载可以更多的往下传递，使复合基础的水平承载能力增大；墙桩长度比较小时，组合基础上部的地下连续墙呈现为刚性状态，类似于“刚性短桩”的力学特性［11］，自身弯曲能力很小。而随着长度比逐渐变大，其自身弯矩能力逐渐增强，呈现出一定的弹性状态。

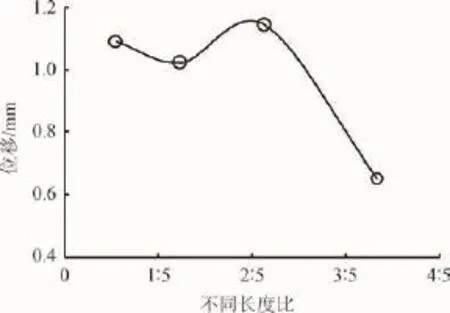
图5 不同长度比影响下位移与长度比的关系曲线图

2.3 竖向荷载对组合基础水平变形和内力的影响

工程上在考虑组合荷载作用下地下连续墙与桩组合基础承载力时，往往是单独分析竖向荷载作用下的承载力以及水平荷载作用下的抗弯性能；相较于单一的受力状态，水平荷载和竖向荷载共同作用时构成的受力系统十分复杂，目前关于竖向荷载对组合基础水平承载力的研究主要采用解析法和数值模拟。

不同竖向荷载影响下组合基础的水平变形和弯矩图如图6所示。由图6（a）可知，组合基础水平位移曲线具有明显的非线性特征；组合基础的水平位移在有竖向荷载作用下相较于无竖向荷载作用下相对减小，反弯点的位置提高了，也说明竖向荷载起到了减小组合基础水平变形的有利作用。

图6 有无竖向荷载影响下组合基础的水平变形和弯矩图

由图6（b）可知：组合基础反向最大弯矩由-810 kN·m增加到-1465 kN·m，此区域可以认为是组合基础抗侧荷载最危险界面；竖向荷载对组合基础的拐点和最大弯矩截面的位置没有产生影响；组合基础顶部竖向荷载作用产生的二次弯矩效应加剧了组合基础中上部区域的弯矩［14］，竖向荷载的存在对组合基础产生一个附加弯矩。

有无竖向荷载影响下组合基础的水平变形和弯矩曲线形成的原因为在上部有竖向荷载作用时，相对于对组合基础顶部增加了一个约束力，这时组合基础的受力状态由纯弯构件压弯构件，竖向荷载引起的压应力可以抵消一部分组合基础的拉应力，因此存在竖向荷载会对水平承载力有所提高［15-16］；在同一水平荷载作用下，有竖向荷载作用的情况其水平位移要比无竖向荷载作用的情况小，说明水平承载力由于竖向荷载的作用而提高。但是，竖向荷载对水平承载力的提高是有限的。由此可知，在工程设计中可充分利用上部竖向荷载对水平承载力有利影响的这一点。

2.4 土体弹性模量对组合基础水平变形和内力的影响

在同一水平力作用下组合基础周边土体的弹性模量发生变化而其它参数不发生任何改变时组合基础水平变形和内力分布规律如图7所示。

图7 土体弹性模量影响下组合基础的弯距图

由图7可知，反弯点的位置并没有发生变化；当组合基础周围土体的弹性模量增大了30%后，组合基础顶部的最大位移缩小了20%，组合基础反方向上的最大弯矩相应地减小了5%；另外，增大周围土体弹性模量对组合基础上部的水平位移影响效果明显比对组合基础下部的影响较显著。从而可知，改变弹性模量对水平变形有影响，但对弯矩的变化影响甚小。

土体弹性模量影响下组合基础的水平变形和弯矩曲土线形成的原因是组合基础周围土体的弹性模量变大，土体的相对刚度也便相应增大，也就是说土层的硬度增强，相当于对土体做了弱加固处理，所以土体侧向绕流的能力减弱；周围土体的弹性模量越大，土体的刚度变大，土体侧移范围和变形越小，组合地基中基础和周围土体产生受到的土体侧压力就越小，从而产生的水平位移变形和应力就越小。影响组合基础水平承载力的土层主要处于浅土层［17］，因此改善组合基础周围土体的弹性模量可以适当地提高组合基础的水平抗力，但对于提高抗弯矩能力效果不是特别显著。

2.5 粘聚力对组合基础水平变形和内力的影响

在同一水平推力作用下组合基础周围土体粘聚力发生变化其它任何参数不发生变化时组合基础位移及弯矩分布如图8所示。

由图8可知，当组合基础的粘聚力由小逐渐变大时，组合基础顶的最大位移值则相反由大逐渐变小，然而这种变化不是很明显趋势很小；随着粘聚力的变大，组合基础的最大弯矩值逐渐减小。具体来讲，组合基础的粘聚力增大了40%时，组合基础顶部的最大位移仅仅减少了2.5%，地下连续墙与桩连接处负弯矩最大值减小了10%；位移和弯矩的反弯点位置几乎没有什么变化。

粘聚力影响下组合基础的水平变形和弯矩曲线形成的原因是粘聚力越小，土体变形越容易进入塑性状态，水平位移也就随之增大；增大粘聚力可以使土体颗粒之间的作用力增大，相互吸附能力更强，从而使组合基础周围土体对组合基础的侧向绕流能力减弱，因此复合基础位移有一定减小，但作用在组合基础上的土压力改变不大，所以对于整体的抗剪切强度影响甚小；随着粘聚力值的逐渐增大，组合基础、土之间的粘结力也越好，滑移位移大大降低，同时屈服极限得到提高［18］。但是从数据分析，粘聚力对组合基础的影响效果不是十分明显，据此可以推断，想通过采用高强度混凝土来提高组合基础的水平承载力和抗弯能力是不理想的。因此，在实际工程中应尽可能采用较低强度等级的混凝土，从而达到节约材料控制成本的目的。

2.6 内摩擦角对组合基础水平变形和内力的影响

内摩擦角分别取12.3、20、30°进行对比分析，其他参数不发生任何变化。在同一水平推力作用下组合基础在内摩擦角影响下的组合基础位移及弯矩分布如图9所示。

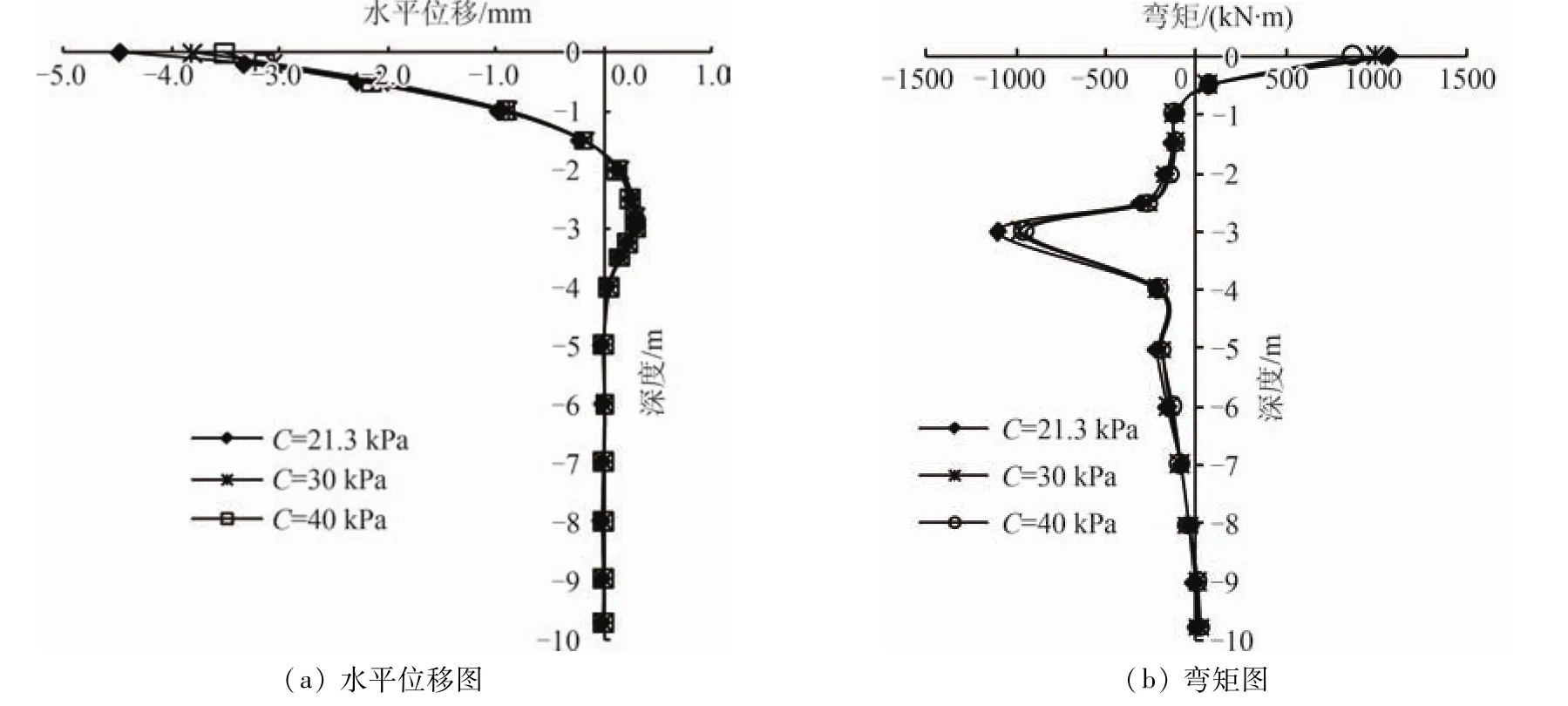
图8 粘聚力影响下组合基础的水平变形和弯距图

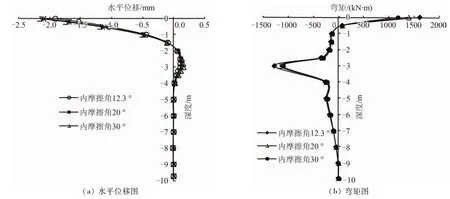
图9 内摩擦角影响下组合基础的水平变形和弯矩图

由图9可知，组合基础周围土体内摩擦角增大而组合基础中地下连续墙与桩的连接处的位移有稍许减小，但是这种趋势只是在组合基础顶部有影响，并且影响十分不明显，其他部位几乎没影响；组合基础的弯矩值随着周围土体内摩擦角的增大只在两个弯矩峰值处减小，反弯点的深度几乎并变化随着内摩擦角的变化而变化［19］。

内摩擦角影响下的组合基础的水平变形和弯矩曲线形成的原因是内摩擦角对组合基础水平变形和弯矩的变化作用原理与粘聚力的情况相类似。增大土体的内摩擦角，可以改善土体颗粒之间的摩擦力，土体颗粒之间相互的嵌入和咬合效果也有所改善，但土体的摩擦强度取决于滑移面上的应力与内摩擦角二者的共同作用，通过数据分析可知，内摩擦角的变化对组合基础的水平变形和弯矩的影响效果不明显，因此在实际工程中土体的内摩擦角可以不作为关键因素考虑。

3 结论

通过上述研究可知：

（1）荷载等级和墙桩长度比是影响新型组合基础水平变形和内力变化的根本因素。新型组合基础中地下连续墙与桩的长度比例问题是工程设计中的重点和难点，墙桩长度比由3∶7变化到4∶6，组合基础呈现出由“刚性短桩”力学特性过渡到弹性状态，表明墙桩长度比4∶6的情况更合理；竖向荷载和弹性模量是组合基础水平变形与内力影响的次要因素；内摩擦角和粘聚力影响效果较弱，对组合基础水平变形和内力改变的作用效果有限。

（2）组合基础顶部以下1/2部分是承担水平变形和内力变化的主要位置，下部抵抗水平荷载的作用很小。地下连续墙与桩组合在一起作为承受水平荷载的基础，发挥地下连续墙水平刚度大的优点，同时也通过下部的桩保证了基础的嵌固。这种组合基础形式符合了变形大的位置增加刚度减小变形、变形小的地方减小刚度节省费用的变刚度设计新理念。水平荷载作用下，相对地下连续墙基础，地下连续墙与桩组合基础可以减小地下连续墙基础的高度和平面尺寸；相对水平受荷桩基础，地下连续墙与桩组合基础可以减小桩数，也符合安全经济绿色的设计理念。

（3）组合基础的弯矩变化规律是上部存在最大正弯矩值，地下连续墙与桩的连接处出现最大负弯矩值，即存在两个最不利影响作用部位，在抗水平荷载组合基础设计中要考虑以上两个部位的最不利影响。

［1］ 谢耀峰.大变位水平承载高桩性状的研究［J］.土木工程学报，2000，33（4）：74-79.

［2］ 刘明虎，付宇文.井筒式地下连续墙基础设计及应用［J］.公路，2006（5）：52-56.

［3］ 吴九江，程谦恭，文华.地下连续墙基础在日本的多样化发展［J］.工业建筑，2013，43（1）：144-149，70.

［4］ 吴九江，程谦恭，文华，等.格栅式地下连续墙竖向载荷模型试验研究［J］.岩石力学与工程学报，2015，34（12）：2580-2592.

［5］ 戴国亮，龚维明，周香琴，等.单室井筒式地下连续墙水平承载力试验与计算方法研究［J］.建筑结构学报，2012，33（9）：67-73.

［6］ 郭河，霍少磊，戴国亮，等.组合荷载作用下井筒式地下连续墙承载特性数值模拟［J］.中外公路，2015，35（1）：1-4.

［7］ 宋章.闭合型地下连续墙桥梁基础承载机理研究［D］.成都：西南交通大学，2008.

［8］ 魏焕卫，崔冠科，宋菲.桩的侧向变形和竖向荷载的耦合分析［J］.结构工程师，2010，26（2）：137-141.

［9］ 魏焕卫，李俊，徐德亭.侧向受荷桩基变形和受力规律的研究［J］.山东建筑大学学报，2010，25（3）：293-296.

［10］费利娅，黄雪峰.水平荷载作用下非饱和黄土嵌岩灌注桩变形规律试验研究［J］.施工技术，2011，40（20）：74-76，97.

［11］陈晓东，柴建峰.黄土地区水平荷载作用下闭合型地下连续墙基础承载性状分析［J］.工程地质学报，2008，16（3）：427-431.

［12］张瑞棋，黄志军.陇东黄土地区刚性地下连续墙桥梁基础水平承载力特性研究［J］.路基工程，2012（3）：97-99.

［13］肖昭然，蒋志娥，赵月平.水平受荷桩的受力特性分析［J］.河南工业大学学报（自然科学版），2005，26（3）：54-56.

［14］吴琼.侧向堆载作用下竖向受荷桩的受力性状［D］.上海：上海交通大学，2011.

［15］赵志鲜.水平荷载作用下挤扩支盘桩的有限元分析［D］.太原：太原理工大学，2007.

［16］蔡忠祥，刘陕南，高承勇，等.基于混凝土损伤模型的灌注桩水平承载性状分析［J］.岩石力学与工程学报，2014，33（z2）：4032-4040.

［17］陈正，梅岭，梅国雄.柔性微型桩水平承载力数值模拟［J］.岩土力学，2011，32（7）：2219-2224.

［18］黄伟达.堆载作用下被动桩与土体相互作用研究［D］.福州：福州大学，2006.

［19］高昂.堆载作用下桩基负摩擦特性分析［D］.北京：清华大学，2012.

Numerical analysis of diaphragm wall-piles combined foundation under lateral loading

Liu Cong1，Wei Huanwei1*，Zhang Wei2，et al.
（1.School of Civil Engineering，Shangdong Jianzhu University，Jinan 250101，China；2.Shandong Electric Power Engineering Consulting Institute，Jinan 250013，China）

Based on the defects of diaphragm wallwith a largematerial，a research ismade on a new type of foundation forms，diaphragm wall-piles combined foundation to provide a theoretical basis for the development of diaphragm wall.For further analysis of the horizontal bearing characteristics of diaphragm wall-piles combined foundation under lateral loading，by using the finite difference software FLAC3D to make simulation，through the research on displacement and moment curve，the paper analyzes the results of diaphragm walls-piles combined foundation under the effect of horizontal force to discuss deformational and stress variation under the influence of factors the basis of forces at different levels，different length ratio，with or without vertical forces，modulus of elasticity，friction angle，cohesion，etc.The results show that Load rating and wall pile length ratio on the level of the composite foundation deformation and internal force changes affect sensitivity，and length of the diaphragm wall-piles design ismore reasonable when the ratio is 4：6.Under the top half part of the combined foundation is the position assumed most of the horizontal deformation and internal force change.The force characteristics of the new combined foundation conform to the new design concept of variable stiffness that at the position of large deformation stiffness increases and deformationdecreases，and at the position of small deformation the stiffness reduces；Two parts of the combined foundation needs to be considered about the adverse effects.

diaphragm wall-pile combined foundation；lateral loading；numerical analysis

TU443

A

1673-7644（2017）01-0047-08

2016-12-25

2014年山东建筑大学横向课题项目（山东电力工程咨询院有限公司，K22014016）

刘聪（1990-），男，在读硕士，主要从事工程岩土体稳定性与支护工程等方面的研究.E-mail：1115705435＠qq.com

*：魏焕卫（1974-），男，副教授，博士，主要从事岩土共同作用和变形控制等方面的研究.E-mail：13181718169＠163.com