一种改进的基于定向天线的移动传感器网络定位算法*

刘震宇,王骥猛

(广东工业大学信息工程学院,广州 510006)



一种改进的基于定向天线的移动传感器网络定位算法*

刘震宇*,王骥猛

(广东工业大学信息工程学院,广州 510006)

针对在无线传感器网络定位中,由于全向天线信号受环境影响而造成定位误差较大的问题,提出了一种改进的基于定向天线的移动无线传感器网络定位算法(DADLP),使用一个带有定向天线的移动锚节点广播位置信息,未知节点接收到信号后,将接收功率平均分为若干等级,缩小定位估计区域。仿真结果表明DADLP算法相对于Ssu、BLI、GGDI和RROI移动锚节点算法提高了定位精度,并且在非规则环境下有更低的平均定位误差。

无线传感器网络;定位;功率分级;移动锚节点;定向天线

无线传感器网络WSN(Wireless Sensor Network)由大量的无线传感器节点组成,是当前备受关注的前沿热点研究领域,广泛应用于环境、军事、生产安全等领域[1]。传感器节点的定位技术是无线传感器网络的关键技术之一,对于传感器网络来说,事件发生的位置是传感器节点监测信息中的重要组成部分,离开了位置信息节点采集的数据毫无意义。

目前,无线传感器网络定位算法可以分为两类:基于测距(Range-based)的定位算法和非测距(Rang-free)的定位算法。基于测距的定位算法需要获取传感器节点间的距离或角度信息,定位精度高,成本高。非测距的定位算法不需要直接测量传感器节点间的距离信息或角度信息,定位精度相对低,对硬件要求低,低功耗,成本低。出于对节点的功耗、传感器网络成本等因素的考虑,和大多数引用场合对传感器节点定位精度要求不高,所以非测距定位更适合大规模网络以及未来发展[2]。

近年来,有大量文献在无线传感器网络中使用移动锚节点的定位算法[3-4],传感器网络定位模块使用天线可以分为两类:定向天线和全向天线。文献[5]中Ssu’s算法是一种经典定位算法。Ssu提出了一种使用锚节点基于几何平分线的定位算法,此算法只需要较少的通信损耗,并且具有较高的定位精度。但是,环境因素对此算法的影响较大。

文献[6]提出了一种使用两个移动锚节点的定位算法,一个作为主定位节点另一个作为辅助节点来完成定位。但是,由于锚节点发送信息会有间隔,所以未知节点接收到的定位锚节点和辅助节点定位信息时的两节点坐标会与它们的理想坐标超前,从而导致未知节点定位后的估计坐标在水平方向上存在误差。在文献[7]中提出了一种基于RSSI的移动锚节点定位算法。但是,此算法锚节点的移动模型为随机轨道模型,无法确保锚节点移动过程中经过同一未知节点多次,造成部分未知节点无法完成定位。

文献[5-7]中提出的定位算法使用全向天线来发射信号,但是,全向天线的射频信号范围大,容易受到外界环境因素的影响,许多算法使用定向天线来定位节点[8-9]。

文献[9]Zhang Baoli提出了3种只使用一个定向天线来定位未知节点的算法BLI、GGDI和RROI。GGDI算法使用定向天线最大增益方向的交点作为未知节点的估计位置,RROI算法使用定向天线的相交区域来求解未知节点坐标,BLI算法虽然是利用相交区域最小的两个移动锚节点坐标估计位置,但是误差较大,误差在30%～40%之间。

众所周知,全向天线的辐射能量范围是360°,这更容易被环境所影响,从而导致更大的定位误差。相比之下,定向天线集中能量在一个较窄的范围内,并且具有更高的增益,通过使用定向天线,一个传感器节点可以有选择的接收只从某些预期方向上的信号,从而避免大部分方向上的环境噪声干扰,达到提高定位精度的目的。如上述研究中,Ssu提出的定位算法中传感器节点使用全向天线来接收信号,而Zhang Baoli提出定位算法中都是使用定向天线来完成定位。Ssu所提出算法的定位误差在40%～65%之间,远大于Zhang所提出的定位算法。

虽然使用定向天线在一定程度上能够避免环境带来的额外误差,但是现实中的定线天线主瓣宽度在60°～120°之间,定向天线的定位相交区域较大。为了减少环境因素对定位的影响,本文提出了一种使用定线天线的定位算法,并且为了进一步缩小定位相交区域,引入了功率分级的思想,以提高定位精度,并进行了软件仿真实验和真实试验以验证该算法的定位精度。

1 问题分析

1.1 Ssu’s算法原理

Ssu’s算法原理:一条弦的垂直平分线会经过这条弦所在圆的圆心。当一个圆上有两条弦时,这两条弦的垂直平分线的交点就是圆心。Ssu把传感器节点的通信范围当作是一个圆,圆上的两条弦是锚节点移动路径,弦的两个端点分别为:第1次和未知节点通信的锚节点位置Nin;最后一次和未知节点通信的锚节点位置Nout。两条弦的垂直平分线的交点即为未知节点的估计位置。如图1(a)所示,

图1 Ssu定位算法

移动锚节点M周期性发射位置信息,在其移动过程中未知节点S在其通信圆内接收到锚节点的信息,端点A、B、C和D为锚节点进入和离开未知节点S的通信范围时的锚节点位置。弦AB和弦CD的垂直平分线交点即为节点S的估计坐标。

1.2 Ssu’s算法误差

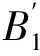
1.3 BLI算法原理

为了减少环境对定位误差的影响,BLI算法采用定向天线进行定位。定向天线能够集中能量在特定的方向上,并且可以缩小射频信号覆盖范围。锚节点在传感器网络中移动,并且周期性发送位置信息,当未知节点接收到第1次通信的锚节点Nin和最后一次通信的锚节点Nout信息时,BLI算法将两锚节点坐标的定向天线辐射边界线的交点作为未知节点的估计坐标。

1.4BLI算法误差

图2 BLI算法

GGDI算法、RROI算法与BLI算法的定位精度相差±5%左右。GGDI算法使用的是定向天线最大增益交点,但是只有一部分未知节点能够接收到最大增益信号,所以受锚节点发送信号间隔影响较大。RROI算法使用Nin和另外一个锚节点坐标(Ni),但是Ni的选择没有一个固定的条件,所以并不能保证Nin和Ni的相交区域最小,RROI的误差相对BLI高5%。

2 DADLP算法

Zhang在BLI方法中采用Nin和Nout作为定位锚节点,与RROI算法相比缩小了相交区域,在一定程度上提高了定位精度。但是,假如能够进一步缩小相交区域,定位精度将会有所提高。例如,在图2中BLI算法所确定相交区域为S1、S2、S3、S4所组成的区域,未知节点S在相交区域的任意位置,假如能够将相交区域划分区域,如图2中S1、S2、S3、S4所组成的区域以虚线弧划分出多个区域,并且确定S属于某一区域,这样就可以缩小S可能存在的区域范围,减小定位误差。

为了进一步缩小定位区域,提高定位精度,本文引入功率分级的思想,提出了一种基于定向天线分级的移动无线传感器定位算法(DADLP),将定向天线按照未知节点接收功率平均分级,选取适当的定位锚节点确定未知节点的坐标。

2.1 接收功率分级

首先,锚节点以固定时间间隔发射信号,未知节点接收到的功率会随着距离的增加而减小,未知节点根据接收到的功率来判断处于某一级处。如图3所示,βm为定向天线夹角,L1与L2为定向天线的辐射边界线,k1和k2为L1、L2的斜率,θ为天线边界与水平线夹角θ=π/2-βm/2,Ni为锚节点移动到第i个位置时的锚节点坐标。定向天线辐射边界线计算公式:

(1)

式中:k1=tan(θ),k2=-k1。例如,未知节点处于第k和k+1等级之间,令节点接收功率为Pr,未知节点到锚节点距离为d则有:

(2)

式中:Pk+1、Pk分别为k等级处最小和最大接收功率,Rk、Rk+1分别为k等级处最小和最大边界半径。

图3 接收功率分级

但是在现实环境中,由于多径、阴影等因素的影响,信号的传输范围通常是不规则的[11],它的不规则性可以用不规则度DOI(DegreeOfIrregular)来说明。若DOI=0,则信号传播范围是一个规则形状,当DOI=0.1,信号的传输距离在[0.9R,1.1R]范围内变化,DOI模型下信号的接收强度表达式:

PR(d)=PT-PL(d0)-10ηlog10(d/d0)ki

(3)

式中:PR(d)为接收信号功率,PT为发送信号功率,PL(d0)为参考距离d0的路径损耗功率,η为路径损耗指数,d为发送端和接收端的距离,ki为不同传播方向上的路径损耗协同系数,ki计算公式:

(4)

式中:rand是均匀产生位于[0,1]上的数值的随机函数。

2.2 锚节点选取

锚节点在移动过程中会形成许多虚拟锚节点,这些虚拟锚节点中有些能够和同一未知节点进行通信。根据几何定理:当两个圆的圆心相距最远时,两个圆的相交区域最小。因此当两个虚拟锚节点相距最远时相交区域最小。如图4所示,在锚节点移动期间能够和未知节点S通信的锚节点位置有若干个,由图4可以看出NDF和NDL的相交区域最小。

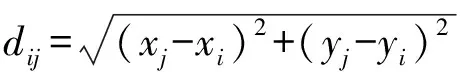
图4 定向天线相交区域

2.3 定位区域分析和位置估计

未知节点根据接收功率的大小,确定其所在等级n,并且选取NDF(x1,y1)和NDL(x2,y2)定位锚节点,如图4中NDF和NDL两锚节点辐射边界线有如下几条:

L1:y-y1=k1(x-x1)

(5)

L2:y-y1=k2(x-x1)

(6)

L3:y-y2=k1(x-x2)

(7)

L4:y-y2=k2(x-x2)

(8)

(9)

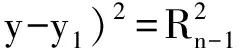
(10)

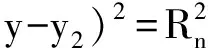
(11)

(12)

式中:L1、L2、L3、L4分别为NDF和NDL定向天线的两辐射边界线,k1、k2、k3、k4分别为定向天线辐射边界线在NDF和NDL处的斜率,A5、A6、A7、A8分别为NDF和NDL在分别在等级为n和n-1的边界弧,并且A5和A6边界弧上点的斜率k应在k1与k2之间,A7和A8边界弧上点的斜率k′在k3与k4之间。取边界线相交区域的质心作为节点的估计位置。质心计算公式如下:

(13)

式中:m为相交区域顶点个数。

2.4 复杂度分析

DADLP算法在计算未知节点估计位置的计算开销共有3种:①直线与直线相交O(1);②直线与圆相交O(2);③圆与圆相交O(3)。其中O(1)需要乘法、加法、减法各2次,O(2)需要10次乘法,加法和减法各4次,O(3)需要18次乘法,加法和减法各6次。由定位区域可知,计算未知节点的估计位置存在两种情况:1,处于一个直线与直线交点,两个直线与圆交点和一个圆与圆交点所组成区域;2,处于两个圆与圆交点和4个直线与圆交点所组成区域;则有未知节点计算开销公式如下:

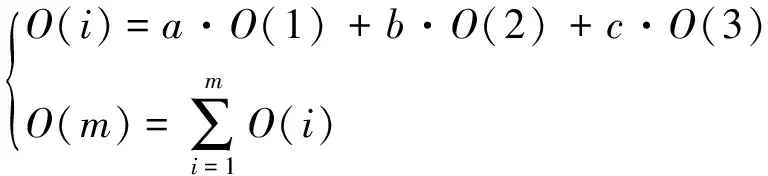
(14)

O(m)为总的计算开销,未知节点i处于n级,N为接收功率分级,θ为定向天线边界线与水平方向夹角,定位锚节点Nin和Nout距离为d。假如d>d0,则a=1、b=2、c=1。否则,a=0、b=4、c=2。d0计算公式如下:

(15)

3 仿真及试验

3.1 仿真实验环境

锚节点的移动有许多模型[12-13]如:随机方向模型、随机路径模型,短距离移动模型等。在文献[9]中BLI算法采用短距离移动路径模型如图5(a)所示。但是,锚节点移动路径在未知节点通信圆上形成的弦都是平行的,Ssu算法是使用两条弦的垂直平分线的交点作为估计坐标的,定位所用的两条弦平行可能会造成弦的交点不存在,许多未知节点不能完成定位,造成定位误差偏大,比较结果有失公平。

图5 移动路径

为了尽量减小弦平行所带来的误差,DADLP算法、Ssu算法、BLI算法、GGDI算法和RROI算法都采用如图5(b)所示移动路径。Ssu算法选取不平行的两条弦,如图5(b)中一条水平的弦和一条斜方向的弦来定位未知节点。这样,DADLP、GGDI、RROI和BLI算法不受路线影响,并且Ssu算法不会因为路线造成额外的误差。

为了验证所提出算法的性能,采用MATLAB为仿真平台进行试验,并选取100×100 m2的二维平面区域作为无线传感器网络定位区域,100个未知节点随机分布在传感网络中,节点通信半径R,节点通信模型使用DOI模型,使用单个装备有定向天线的移动锚节点按照移动路径移动,锚节点发送信号时间间隔为t,n为定向天线功率级数。定位精度用平均定位误差er来衡量:

(16)

3.2 不同等级下定位误差

在规则模型下,锚节点以固定速度移动,信号发送间隔t=0.1/s环境下,当n在[2,16]之间时,R=10 m、15 m、20 m、25 m时定位误差如图6所示。从图6可以看出随着定向天线功率等级增大,定位误差呈下降趋势。随着通信半径的增大,定位误差呈明显增大趋势。这是因为当通信半径相同时,等级越大定向天线每一级所占的环形区域就越小,因此NDF和NDL坐标处的定向天线的相交区域就越小。同样,在等级相同时,半径较小所以相交区域也较小,因此取相交区域的质心就越接近未知节点的真实坐标。

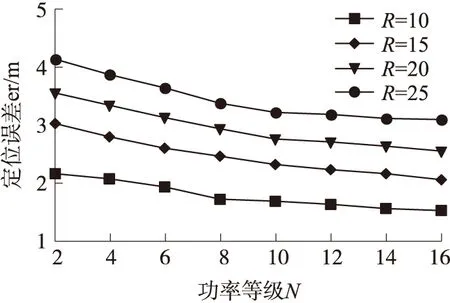
图6 不同功率等级下的定位误差

3.3 不同时间间隔下定位误差

DADLP与其他4种算法在锚节点以相同固定速度下移动,DOI=0,信号发送间隔t在[0,1]之间的误差比较。如图7所示,DADLP算法与其他4种算法相比定位精度高。Ssu的算法的定位误差受发送信号间隔影响较大,这是由于噪声环境中锚节点的发送信号间隔时间越长所产生的虚拟锚节点越少,所以Nin和Nout坐标与理论上确定弦的两个端点位置误差较大。未知节点能够接收到定向天线最大增益处信号的只有一部分,所以GGDI算法定位精度有限。RROI算法定向天线的相交区域较大,所以定位误差大。BLI算法使用定向天线的交点作为未知节点估计位置,使用一个辐射边界线交点来代替整个相交区域,误差在30%～40%。

图7 不同发射间隔下定位误差

3.4 不同DOI下定位误差

由于多径噪声等的影响,不规则度通常是变化的。如图8所示是5种算法分别在不同DOI环境下对定位误差的影响。由图8可知随着DOI的值的增大,5种算法的定位误差都在一定程度上增大,DADLP算法定位误差远小于其他几种算法,定位误差相差至少1.1 m。

图8 不同DOI下的定位误差

3.5 模拟试验

为了验证DADLP算法在现实环境中的性能,现对其进行试验以评估DADLP定位算法性能。由于DADLP算法采用的是移动锚节点是装备在机器人身上的,所以试验采用ESP8266WIFI模块,发射功率采用802.11b模式下16 dBm的输出功率,如图9所示两个WIFI模块相隔10 m放在地面上,WIFI模块1固定发射信号WIFI模块2接收信号,试验20次后得到不同距离下的平均接收功率如表1所示。

图9 真实试验

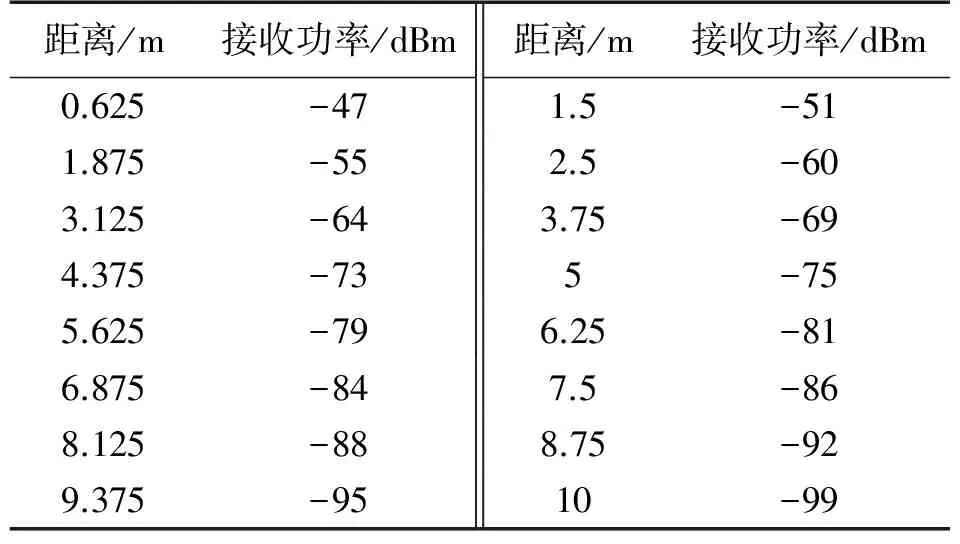
距离/m接收功率/dBm距离/m接收功率/dBm0．625-471．5-511．875-552．5-603．125-643．75-694．375-735-755．625-796．25-816．875-847．5-868．125-888．75-929．375-9510-99

图10 不同发射间隔下的定位误差

算法试验分为两个阶段,第1阶段是接收功率的采集阶段,未知节点周期性地采集接收功率。第2阶段是利用DADLP定位算法对未知节点进行定位。试验在通信半径为10 m,不同信号发送间隔t下的定位误差如图10所示。不同半径下的定位误差如图11所示。随着半径的增大在相同功率等级下DADLP算法定位误差逐渐减小,并且在相同等级下半径越小,定位精度越高,试验结果与理论分析结果相符。

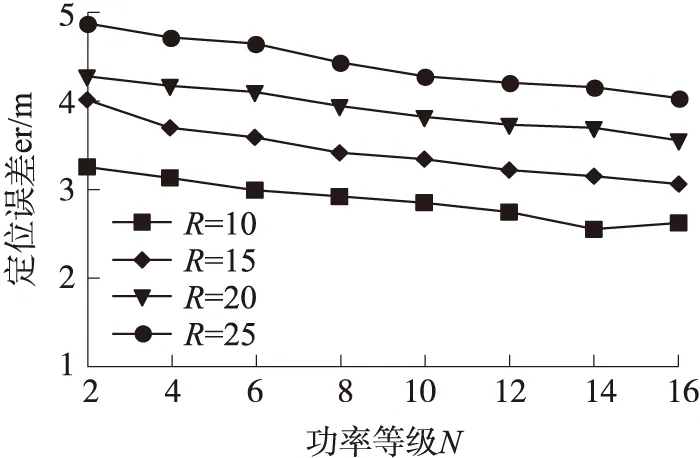
图11 不同半径下的定位误差

4 结论

DADLP算法使用一个移动锚节点周期性发射定位信息,将接受功率分级,根据未知节点接收功率确定其所处等级,进一步缩小定位锚节点的相交区域,从而确定未知节点坐标。DADLP算法与Ssu的算法、GGDI算法、RROI算法和BLI算法进行比较,仿真结果表明在规则和非规则模型下,定位误差都低于其他几种算法,DADLP算法具有更好的定位效果。

[1] 彭宇,王丹.无线传感器网络定位技术综述[J]. 电子测量与仪器学报,2011,25(5):389-399.

[2] 范时平,罗丹,刘艳林.基于跳距与改进粒子群算法的DV-Hop定位算法[J]. 传感技术学报,2016,29(9):1410-1415.

[3] Ou C H,He W L. Path Planning Algorithm for Mobile Anchor-Based Localization in Wireless Sensor Networks[J]. IEEE Sensors Journal,2013,13(2):466-475.

[4] Abdi F,Haghighat A T. A Hybrid RSSI Based Localization Algorithm for WSN Using a Mobile Anchor Node[C]//Computing Communication and Networking Technologies(ICCCNT). International Conference on IEEE,2014:1-6.

[5] Ssu K F,Ou C H,Jiau H C. Localization with Mobile Anchor Points in Wireless Sensor Networks[J]. IEEE Transactions on Vehicular Technology,2005,54(3):1187-1197.

[6] Shi Z,Zhu Y,Shi J,et al. A Localization Scheme with Dual Mobile Beacons in Wireless Sensor Networks[J]. Information Technology Journal,2013,12(12):2426-2432.

[7] Fan C W,Wu Y H,Chen W M. RSSI-Based Localization for Wireless Sensor Networks with a Mobile Beacon[C]//Sensors,2012 IEEE.IEEE,2012:1-4.

[8] Wu Y H,Chen W M. Localization of Wireless Sensor Networks Using a Moving Beacon with a Direction Antenna[C]//High Performance Computing and Communications,11th International Conference on. IEEE,2009:237-242.

[9] Zhang B,Yu F. LSWD:Localization Scheme for Wireless Sensor Networks Using Directional Antenna[J]. IEEE Transactions on Consumer Electronics,2010,56(4):2208-2216.

[10] Zhang B,Yu F,Zhang Z. An Improved Localization Algorithm for Wireless Sensor Network Using a Mobile Anchor Node[C]//Information Processing Asia-Pacific Conference on. IEEE,2009:485-488.

[11] 王承林. 基于边界盒节点定位算法的研究[D]. 东北大学,2012.

[12] Rezazadeh J,Moradi M,Ismail A S,et al. Superior Path Planning Mechanism for Mobile Beacon-Assisted Localization in Wireless Sensor Networks[J]. IEEE Sensors Journal,2014,14(9):3052-3064.

[13] Han G,Chao J,Zhang C,et al. The Impacts of Mobility Models on DV-Hop Based Localization in Mobile Wireless Sensor Networks[J]. Journal of Network and Computer Applications,2014,42:70-79.

刘震宇(1976-),男,博士,广东工业大学副研究员.研究领域数字信号处理、物联网技术和通信网安全处理,zhenyuliu@gdut.edu.cn;

王骥猛(1990-),男,硕士研究生.研究方向为无线传感器网络定位,a19880830@qq.com。

An Improved Localization Algorithm for Mobile Sensor Network Using Directional Antenna*

LIUZhenyu*,WANGJimeng

(School of Information Engineering,Guangdong University of Technology,Guangzhou 510006,China)

To solve the signal from an omni-directional antenna of mobile wireless sensor networks is affected by environment noise caused a big localization error problem,an improved localization algorithm(DADLP)using a mobile anchor node equipped with a direction antenna was proposed. The received power of sensor node is divided into several levels to reduce the estimated area and improve the localization accuracy. The simulation results show that DADLP has higher accuracy and lower average localization error than Ssu’s algorithm,BLI algorithm,GGDI algorithm and RROI algorithm in irregular environment.

wireless sensor networks;localization;different level of power;mobile anchor node;direction antenna

项目来源:国家自然科学基金项目(61401106);广州市科技计划项目科学研究专项(2014J4100206)

2016-07-17 修改日期:2016-11-21

TP393

A

1004-1699(2017)03-0456-07

C:7230

10.3969/j.issn.1004-1699.2017.03.020