一阶隐方程转化为显方程的统一方法
曾菊华
(赣州师范高等专科学校 数学系,江西 赣州 341000)
一阶隐方程转化为显方程的统一方法
曾菊华
(赣州师范高等专科学校 数学系,江西 赣州 341000)
一阶隐方程转化为显方程的两种方法本质上是相同的,可以概括为:把一阶隐方程F(x,y,y′)=0表示成参数形式x=Φ(s,t),y=φ(s,t),y′=ψ(s,t)(s,t是参数,Φ(s,t),φ(s,t),ψ(s,t)具有连续的一阶偏导数),代入恒等式dy=y′dx,即得关于s,t的一阶显方程.
常微分方程;隐方程;显方程;微分法;参数表示
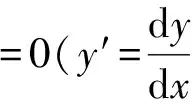
1 一阶隐方程转化为显方程的两种方法
以文献[1]为例,其在“一阶隐式微分方程与参数表示”中介绍的方法可简述如下.
1.1 类型I(解出y或x)y=f(x,y′) 或x=f(y,y′)

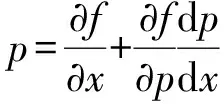
(1)
这个方法被称为微分法.
1.2 类型Ⅱ(不显含y或x)F(x,y′)=0或F(y,y′)=0

x=φ(t),p=ψ(t),
(2)
代入恒等式dy=pdx即得
dy=ψ(t)φ′(t)dt.
(3)
这是关于y,t的一阶显方程.
对于这样的解法,学生理解起来并不容易,他们往往觉得这是两种完全不同的方法,并且想当然地误以为不属于以上两种类型的一阶隐方程是不能转化为显方程的.
2 两种方法的统一
上述的两种方法本质上是相同的,可以统一概括为下面的通法:
把一阶隐方程F(x,y,y′)=0表示成适当的参数形式
x=Φ(s,t),y=φ(s,t),y′=ψ(s,t),
(4)
其中s,t是参数,Φ(s,t),φ(s,t),ψ(s,t)具有连续的一阶偏导数,代入恒等式dy=y′dx,即得关于s,t的一阶显方程(这一点只需作简单的微分运算即可得证,读者不妨一试).
特别地,方程y=f(x,y′)可表示成以x,p为参数的参数形式x=x,y′=p,y=f(x,p)(固定的表示方法),而接下来代入恒等式dy=y′dx,与微分法中的“在y=f(x,p)两边对x求导”实质上是一回事;方程F(x,y′)=0可表示成单参数的参数形式x=φ(t),y′=ψ(t)(具体表示形式需要根据方程特点灵活选择),这样就成了前述两种类型的隐方程的转化方法了.
这个统一方法易记易懂,它揭示了教材中介绍的两种方法的本质.
例1 求微分方程(2-y′)2+y2y′=y2的通解.
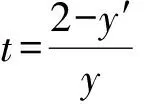
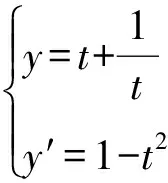
(5)
代入恒等式dy=y′dx,得

(6)

(7)

(8)
所以原方程的通解(参数形式)是

(9)

注:t2=1时,将得方程的两个特解y=±2.
例2 解微分方程(xy′)2+xy′lnx-y=0.
解法1 方程可写成y=(xy′)2+xy′lnx,属于解出y的类型,因而可表示成参数形式
x=x,y′=p,y=(xp)2+xplnx,
(10)
代入恒等式dy=y′dx,并整理,得到关于x,p的一阶显方程
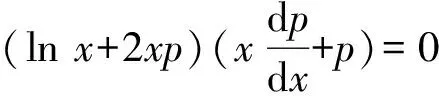
(11)
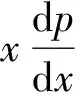
解法2 观察方程的特点,可令xy′=s,lnx=t,那么方程可表示成参数形式
x=et,y′=se-t,y=st+s2.
(12)
代入恒等式dy=y′dx得到关于s,t的一阶显方程d(st+s2)=sdt,也即

(13)
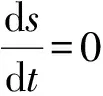


(14)
这里的解法2是通法,适用于求解任意的一阶隐方程,其关键在于采用的方程的参数形式要适当,以使后续计算简便.
[1] 王高雄,周之铭,王寿松,等.常微分方程[M].3版.北京:高等教育出版社,2006:62-69.
[2] 周义仓,靳祯,秦军林.常微分方程及其应用[M].2版.北京:科学出版社,2015:52-60.
[3] 楼卫红,林伟.常微分方程[M].上海:复旦大学出版社,2007:43-50.
[4] 化存才,赵奎奇,杨慧,等.常微分方程解法与建模应用选讲[M].北京:科学出版社,2009:37-43.
[5] 东北师范大学微分方程教研室.常微分方程[M].2版.北京:高等教育出版社,2005:39-46.
A Unified Approach to the Transformation of Implicit Differential Equation into Explicit Differential Equation
ZENG Juhua
(DepartmentofMathematics,GanzhouNormalCollege,Ganzhou341000,China)
Usually, there are two methods of transforming a first order implicit equation into an explicit differential equation. But, they are essentially the same, and can be summarized as: let the first order implicit differential equationF(x,y,y′)=0 expressed as a parametric form,x=Φ(s,t),y=φ(s,t),y′=ψ(s,t)(s,tare parameters, andΦ(s,t),φ(s,t),ψ(s,t) have continuous first order partial derivatives respectively). Then, by the identity dy=y′dx, get a first order implicit differential equation.
ordinary differential equation; implicit differential equation; explicit differential equation; differentiation method; parametric representation
2016-12-12
江西省高等学校教学改革研究省级立项课题 (JXJG-11-93-1)
曾菊华(1972—),男,江西信丰人,赣州师范高等专科学校数学系教授,主要研究方向:数学教学论.
10.3969/j.issn.1007-0834.2017.01.002
O29
A
1007-0834(2017)01-0006-03

