蜂群算法在冷链物流配送车路径规划中的应用

白焘++李鸣++严良涛

摘要：车辆路径规划问题是冷链物流配送环节的关键，而易腐农产品会随运输时间的推移而腐烂变质或者影响其使用价值。利用解蜂群算法采蜜行为的基本原理及其算法流程，根据配送中心与客户的需求以及运输过程存在各方面约束条件的情况下建立模型并初步考虑到农产品的腐败成本。最终分析并设计了一种基于人工蜂群算法的冷链物流配送车辆路径优化方法，并应用实例及软件仿真对算法进行了验证，且证明了该算法的有效性。

关键词：冷链物流；蜂群算法；路径优化；腐败成本；有效性

中图分类号：TP301.6 文献标识码：A 文章编号：0439-8114（2016）22-5958-04

DOI：10.14088/j.cnki.issn0439-8114.2016.22.057

Application of Colony Algorithm in Vehicle Routing Planing of Cold-chain Logistics

BAI Tao，LI Ming，YAN Liang-tao

（School of Mechanical & Electrical Engineering， Nanchang University， Nanchang 330031， China）

Abstract：Vehicle routing planing is the key step of cold-chain logistics， however， perishable agricultural products will be bad and affect its use value with the transport time. Based on the basic principle of colony algorithm with honey behavior and algorithm of process， then the model was establish and preliminary given the cost of corruption based on distribution center with the needs of customers and various aspects of constraint condition in the process of transportation. Final analysis and design an algorithm based on artificial colony of cold-chain logistics distribution vehicle routing optimization method， then through software simulation of algorithm to wake the validation and prove its validity.

Key words： cold-chain logistics； colony algorithm； routing planing； cost of corruption； validity

随着中国经济的发展，生活水平不断提高，为保证冷冻食品的质量，冷链物流快速发展。有效的配送却成了冷链物流的关键环节，因为农产品受自然条件的影响较大，容易腐坏，所以要求配送车辆效率的提升，实现资源的优化配置，减少农产品的损失。本研究设计实现了一种基于人工蜂群算法的冷链物流配送车辆路径优化算法，蜂群具有劳动分工和协作机制，蜜蜂按照劳动分工采用不同的搜索策略或模式，并且可以互相共同完成寻优工作，且全局寻优能力强[1]。基于采蜜行为的蜂群算法能利用蜜蜂之间寻优的正反馈机制，有效加快了全局寻优的过程，同时发现蜂群算法在搜索过程中能自组织进行角色变换，具有很强的自组织、自适应以及鲁棒性强等特点。基于蜂群采蜜行为算法对冷链物流配送车辆路径规划实现了智能化，使物流配送服务的质量，提高了物流配送的合理性和高效性、提高了服务资源利用率、降低了物流服务成本，最终保证了冷冻食品的质量与安全。

1 人工蜂群算法

1.1 蜜蜂采蜜行为生物学机理

蜂群算法是一种群智能优化算法，是通过对自然界中蜜蜂采蜜的行为进行的模拟算法。蜜蜂能在苛刻和复杂的环境中进行高收益率的采蜜，并且能够自发进行角色互换，随着环境的改变而变换自己的采蜜方式最终快速地找到优质的蜜源。Karaboga等[2，3]通过对蜜蜂采食行为的研究给出了人工蜂算法模型，模型由3个基本要素组成：蜜源、雇佣蜂、非雇佣蜂。

蜜源：蜜蜂的搜索目标，离蜂巢的距离远近、花蜜的丰富程度、获取花粉的难易程度等由多方面因素评价其质量，蜜源的质量与收益度成正比。

雇佣蜂：也被称为引领蜂，其数量与蜜源的数量相对应，自身还储存蜜源的相关信息。回到蜂巢中时会通过摇摆舞的形式按一定的概率与其他蜜蜂分享自身携带食物源的信息。

非雇佣蜂：非雇佣蜂有两种，分别是跟随蜂与侦察蜂。主要目的是开采蜜源和发掘新的蜜源，跟随蜂按一定的概率从引领蜂那获取蜜源的信息。

刚开始，所有蜜蜂都可以看做是侦察蜂，然后根据以往的经验决定其搜索方式。经过一系列搜索后，如果侦察蜂找到某个蜜源，侦察蜂就开始进行采集花蜜利用自身的储存功能标记食物源的信息。同时，侦察蜂将成为雇佣蜂（引领蜂）。蜜蜂采完蜜后将蜂蜜放在蜂巢然后将有以下几种选择。

1）如果蜜源收益度低，放弃蜜源再次成為侦查蜂或者跟随蜂。

2）如果蜜源收益度仍然很好，引领蜂通过跳摇摆舞招募更多的蜜蜂采集蜜源，接着继续去蜜源采蜜。

3）如果蜜源收益度一般，继续在之前侦查蜜源采蜜并且不进行招募活动。

1.2 ABC算法简介

ABC算法是一个迭代寻优算法，初始时随机生成N个蜜源（问题的可行解）{X1，X2，X3…XN}是一个D维向量，一个采蜜蜂对应一个蜜源。

采蜜阶段，每只雇佣蜂在每一个蜜源的领域内生成一个新的蜜源，并且评估两者的花蜜数量（适应度），保留适应度高的蜜源，蜜源的更新公式为：

vij=xij+rand（xij-xkj） （1）

其中，k∈{1，2，…N}，j∈{1，2，…D}；rand是0到1之间的一个随机数，控制一个蜜源的领域生成范围。

跟随阶段，当所有的雇佣蜂完成这个过程后，它们与跟随蜂共享蜜源的信息。每個跟随蜂按照一定的概率选择一个蜜源。

引领蜂招募跟随蜂概率为：

Pi=fi/■fi （2）

式中，fi是第i个解的适应度，适应度越高的蜜源被选择的概率越大。

若食物源经过若干次搜索后，没有得要最优解，那么认为这个解陷入僵局放弃此解，该食物源将被引领蜂放弃，自己的角色将转化成侦察蜂。然后随机产生一个新的解代替淘汰解，这样算法能够跳出局部最优解，加快算法的收敛速度。

xji=xjmin+rand（0，1）（xjmax-xjmin） （3）

其中，k∈{1，2，…N}，j∈{1，2，…D}，xmax、xmin为个体的最大最小值。

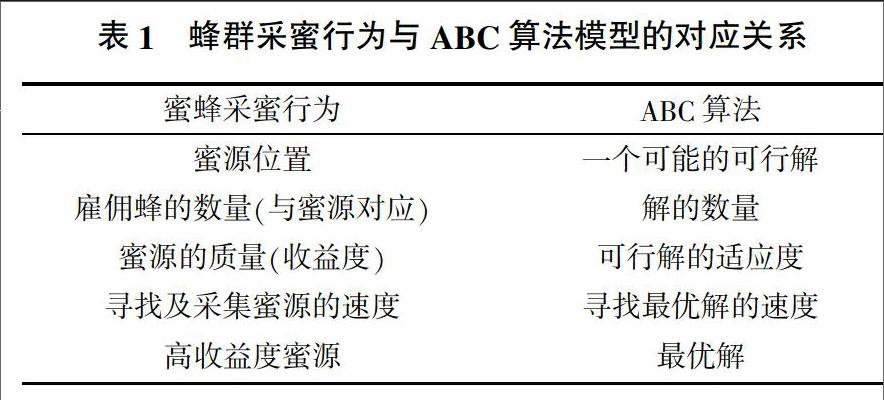
为了更好理解该算法，现将蜜蜂采蜜行为与算法的对应关系如表1所示。

2 蜂群算法在路径优化上的应用

2.1 数学模型

随着时间的推移，农产品容易腐烂变质，农产品冷链物流的配送，除了要满足客户对于货物送达的基本要求，还应当尽量满足客户对于配送时间的要求，从而对农产品的新鲜度有一定的保障[4]。因此，本研究选取了更为接近实际情况的车辆路径问题（Vehicle Routing Problem，VRP）进行研究。

VRP模型是物流配送优化中的关键问题[5]。冷链物流配送问题可以描述为，在约束条件下，设计从一个配送中心出发，到多个已知客户位置的多条最优送货路径回路，即要设计多条总体配送成本（车辆管理费用+运输成本+运输中产品产生的腐败成本）最小的路线且满足：

1）每个城市或者客户只被一辆车访问一次[6]；

2）所有车辆从起点出发最终回到起点；

3）满足一些约束条件。

通常的约束包括：每辆车的载重量限制、到达客户的时间限制（具体表现在农产品的腐败成本上与时间有关，耽搁时间越长农产品价值越低，成本越高），这里假定所有车辆都一样且有相同的载重量。

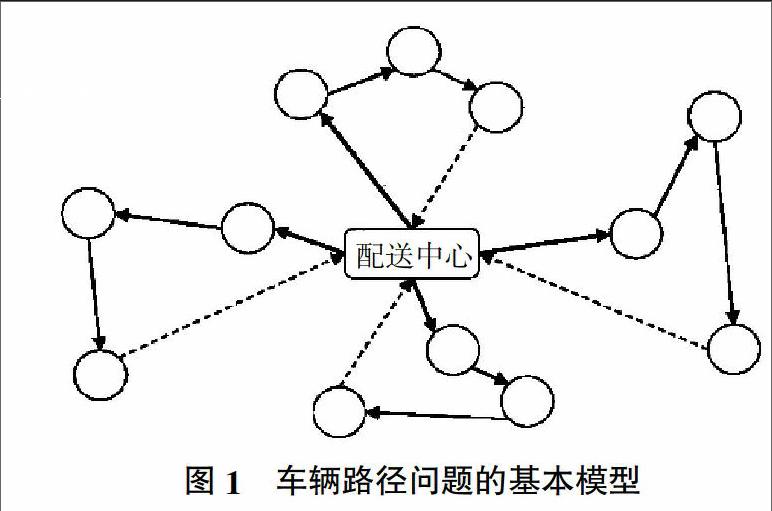
其基本模型如图1所示，实线代表载货运输，虚线代表空车行驶，圆圈代表各个客户[7]。

记G=（V，E）为赋权图，V={1，2，3……，n}为顶点集，代表所有的客户位置及配送中心；E为边集，代表各个顶点的距离为lij（lij>0，lii=0；i，j∈V），每一辆车的载重量为M，各个客户需求量为mi（i∈V），并且定义变量如下：

yki1，客户i的需求由车辆k完成0，其他 （4）

xijk1，车辆k从i点行驶到j点0，其他 （5）

约束条件为：

■yki=1，i∈V （6）

式6保证每一个客户只被访问一次

■xijk=ykj，i∈V，？坌k■xijk=yki，i∈V，？坌k■■xijk≤|S|-1，S？哿V （7）

其中，xijk，yki≤（0，1）；i，j∈V，？坌k，|S|为集合S中所含图G的顶点个数。

式7保证车辆能够回到起点形成回路，且路径连接条数必小于等于顶点数减一。

腐败成本P（t）的计算。由于不考虑农产品在配送中心的腐败损失，以出发时完好的物品量Wi（0）为计算腐败成本的标准量，由于腐败速率恒定，有腐败微分方程[8]：

■=-？兹Wi（t） （8）

其中，Wi（t）为运往客户i的路途中t时刻完好的产品量，？兹为腐败速率系数，不考虑其他因素，恒定不变。

假设ti为配送中心到达客户i所需要的时间，a为运输速度的倒数，li为配送中心到客户i的距离，di为客户i的需求量，则有：

ti=ali；Wi（t）=di （9）

将上式带入微分方程得：

Wi（0）=dieti？兹 （10）

则产品运输到客户i后的腐败量为

Wi（0）-Wi（t）=di（eti？兹-1） （11）

易腐农产品的单价为c，则产品运到客户i的腐败成本为

P（t）=c*di（eti？兹-1） （12）

则目标函数如下：MinU=A*（maxk）+P（t）+h*（■■■1ijxijk） （13）

A*（maxk）表示车辆的管理费用，A表示每一辆车的管理费用。

P（t）表示产品的腐败成本，与时间有关系。

h*（■■■1ijxijk）表示运输费用，h表示单位长度路程费用。

2.2 路径优化算法设计与实现

首先对食物源（客户）采取实数编码，可以用自然数I∈{1，2，…N}表示客户，0代表物流配送中心，路径的表示方法则更为简单，例如0-1-2-3-0，表示车辆从配送中心出发，经过客户1、客户2、客户3，最终回到配送中心。然而有时候车辆较多无法区分时，则用负数表示物流车辆，k∈{-1，-2，…-M}，则路径（-1）-1-2-3-（-2）-3-4-（-2），表示第一辆车从配送中心出发，经过客户1、客户2、客户3，最终回到配送中心；第2辆车经过客户3、客户4回到配送中心，表示两个车辆的回路。初始解的生成将车辆序号插入到客户编号序列里面，生成初始解。主要步骤描述如下。

①对算法中需要的参数设定。算法中主要的参数：种群大小NP，雇佣蜂数En，跟随蜂数On，侦察蜂数Sn，局部最大搜索次数Limit，迭代次数Cycle，解的D（维度），客户数（N）、车辆数（K），其中，D=N+K[9]。

②初始化蜂群数量。随机生成N个预行驶路线（即客户车辆的编号序列），构成预行驶路线的方法为：随机选择一辆车，将其编号插入到序列的第一位，从这一位开始向后逐一判断车辆的载重是否能够满足后面客户的需求，直到不能满足时再从剩下的车辆中随机选择一辆车，将其编号插入到该位置。

③根据车辆的载重量客户的时间限制及一些约束条件，确定生成的解是否满足条件，当生成的解不满足约束时重新生成新的解，并根據设计的目标函数Min U对各解的适应度值进行计算，然后存储这些信息。

④开始算法的迭代过程，重复执行步骤⑤～步骤⑧。

⑤遍历所有的解，在解的邻域内寻找新解，保留原解和新解中适应度值更高的解。

⑥根据所有解的适应度值来计算各个解被选择的概率值。

⑦当达到局部最大次数时，解没有被更新，则将该解丢弃，重新生成一个解来代替且记录目前为止的最优解。

⑧判断是否已经达到全局最大循环次数，到达则算法结束，否则转到步骤⑦中记录的解即为全局最优解。

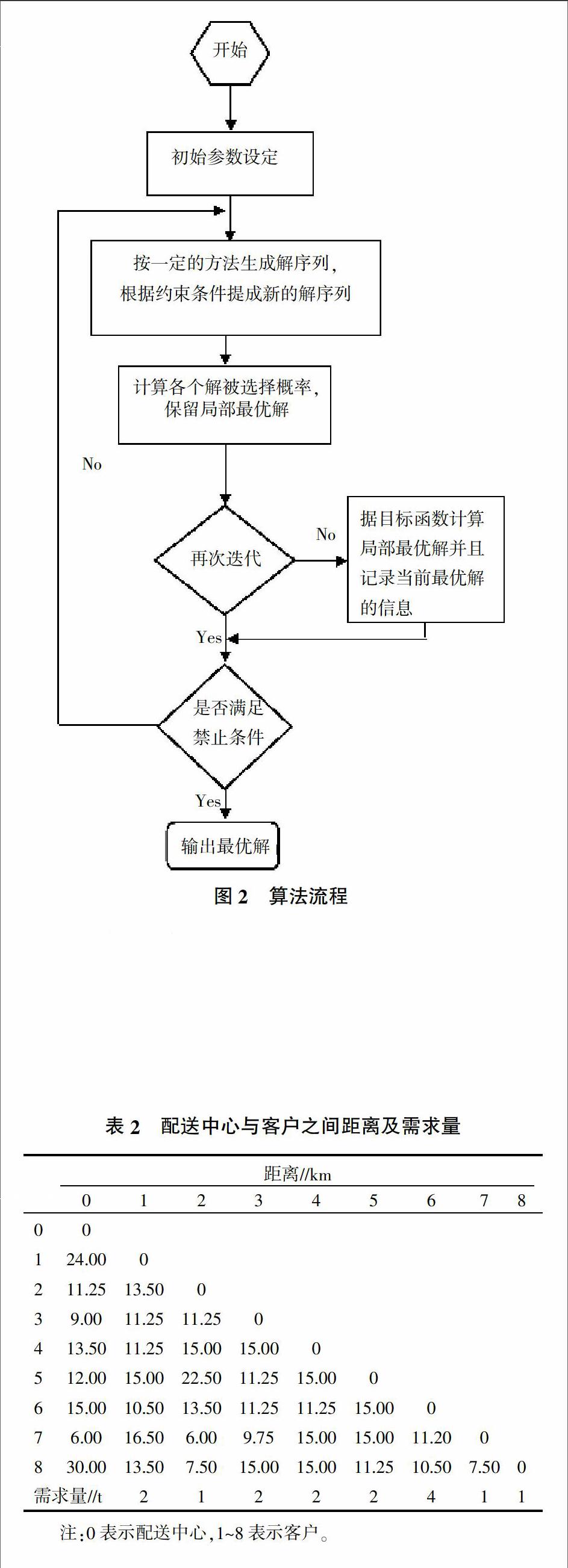
算法流程图如图2所示。

3 实例求解与分析

一个配送中心，配送物流车总数为2，客户数为8，车辆的载重为8 t。客户与配送中心的距离及客户与客户之间的距离且各个客户的需求量如表2所示。假设车辆的行驶速度一定，交通状况良好，运输时间与运输路程当然也就成正比关系，腐败成本与时间成正相关，即车辆行驶总路程与腐败成本成正相关关系。参数设置种群规模为60，迭代次数为50（与文献[10-12]的设置相同）。经过10次运算，得到的计算结果见表3。从表3中可以看出，10次运行得到的结果在第4次得到了最优解101.25 km，其对应配送路径为0→4→1→6→0；0→7→2→8→5→3→0。结果表明，ABC算法有较好的优化能力，适合解决VRP问题，可以方便有效地求得问题的最优解或近似最优解[13-20]。

4 小结

利用蜂群算法，以物流成本为最终目标，对车辆路径进行了优化，在冷链物流配送系统中，实现了资源的优化配置，农产品的保鲜度得到了保障，提高了经济效益。通过仿真表明，用该算法解决车辆路径问题是有效可行的。

参考文献：

[1] 张超群，郑建国，王 祥.蜂群算法研究综述[J].计算机应用研究，2011，28（9）：3201-3204.

[2] KARABOGA D.An idea based on honey bee swarm for numerical optimization[R]. Kayseri：Erciyes University，2005.

[3] KARABOGA D，BASTURK B.A powerful and efficient algorithm for numerical function optimization： Artificial bee colony（ABC） algorithm[J].Journal of Global Optimization，2007，39（3）：459-471.

[4] 李明泽.蜂群算法研究综述.城市农产品冷链物流配送路径优化研究[D].辽宁大连：大连海事大学，2013.

[5] 崔雪丽，马 良，范炳全.车辆路径问题（VRP）的蚂蚁搜索算法[J].系统工程学报，2004，19（4）：418-422.

[6] 杨 进，马 良.蜂群优化算法在车辆路径问题中的应用[J].计算机工程与应用，2010，46（5）：214-216.

[7] 李 芳，罗清明，叶春明.JIT方式在冷链物流配送中的应用研究[J].工业技术经济，2007，26（1）：99-101.

[8] 李 磊，张彦玲.易腐农产品配送中心选址问题[J].江南大学学报，2013，12（6）：732-738.

[9] 张英伟.基于人工蜂群算法的城市物流配送服务车辆调度问题研究[D].哈尔滨：哈尔滨工业大学，2014.

[10] 赵燕伟，吴 斌，蒋 丽，等.车辆路径问题的双种群遗传算法求解方法[J].计算机集成制造系统，2004，10（3）：303-306.

[11] 姜昌华，戴树贵，胡幼华.求解车辆路径问题的混合遗传算法[J].计算机集成制造系统，2007，13（10）：2047-2052.

[12] 肖健梅，李军军，王锡淮.求解车辆路径问题的改进微粒群优化算法[J].计算机集成制造系统，2005，11（4）：557-581.

[13] 陈阿慧，李艳娟，郭继峰.人工蜂群算法综述[J].智能计算机与应用，2014，4（6）：20-24.

[14] 杨 进，马 良.蜂群优化算法在带软时间的车辆路径问题中的应用[J].预测，2010，29：85-86.

[15] 王连稳，蔡延光.基于蜂群算法的随机需求车辆路径优化问题研究[J].科研发展，2013（6）：85-87.

[16] 王志刚，夏慧明.求解车辆路径问题的人工蜂群算法[J].计算机工程与科学，2014，36（6）：1088-1093.

[17] 张丽萍，柴跃廷.车辆路径问题的改进遗传算法[J].计算机集成制造系统，2002，8（6）：451-454.

[18] 王晓博，李一军.多车场多车型装卸混合车辆路径问题研究[J].控制与决策，2009，24（12）：1769-1774.

[19] 秦全德，程 适，李 丽，等.人工蜂群算法研究综述[J].智能系统学报，2014，9（2）：377-385.

[20] 段风华.带软时间窗约束的开放式车辆路径问题及其应用[D]. 长沙：中南大学，2009.