基于改进的马尔科夫链模型的河流径流预测研究

刘晓哲

（辽宁省水文局，辽宁沈阳110003）

基于改进的马尔科夫链模型的河流径流预测研究

刘晓哲

（辽宁省水文局，辽宁沈阳110003）

针对传统马尔科夫链模型不能考虑各因子权重的局限，文章引入自相关系数作为各因子权重，对传统马尔科夫链模型进行改进，并将改进的马尔科夫链模型进行径流预测。研究结果表明：改进马尔科夫链模型可提高方程的收敛性和预测精度，改进的马尔科夫链模型径流预测精度明显好于传统马尔科夫链模型的预测精度，预测值与实测值相关系数高于传统马尔科夫链模型。研究成果对于区域径流的数学模型预测具有较好的参考价值。

改进马尔科夫链模型；传统马尔科夫链模型；加权权重；径流预测

马尔科夫链模型可以表述随机系列的动态变化，可通过不同变量之间的状态变化的转移概率来预测系统未来的变化。由于模型具有明确的数学意义，当前被广泛用于不同变量的预测。近些年来，随着计算技术的不断发展，数学模型也不断地被用于水文序列变量的模拟预测，并取得一定的研究成果［1-6］。这些数学模型包括灰色系统模型、神经网络模型法以及其他时间序列模型法，但在这些模型中，马尔科夫链模型可以通过不同变量之间的转移概率来反映不同随机变量之间的影响程度，可以较好的模拟不同状态变量之间的相互联系，近些年来，被许多学者应用于水文序列的模拟中，取得较好的预测模拟成果［7-10］。但这些成果都表明马尔科夫链模型存在收敛精度不高，且未能考虑不同因子之间的权重，为此有学者对传统马尔科夫链模型进行改进，引入权重系数，对各个因子设定不同的权重，提高了模型的收敛精度以及变量预测的精度。但改进的马尔科夫链模型只是对降水系列进行了模拟，还未在天然径流进行预测，而天然径流是水资源评价的重要依据。为此本文引入改进的马尔科夫链模型，结合水文站还原的天然径流资料，对比分析改进的马尔科夫链模型和传统的马尔科夫链模型的径流预测精度。研究结果对于数学模型在流域径流中的应用研究提供参考价值。

1 加权马尔科夫链模型原理

1.1 马尔科夫链

马尔科夫链先计算一组随机变量序列，｛x，t∈ T｝为随机生成的一组随机序列，在随机序列中，

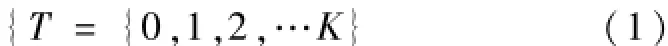
对于任意时间变量t≥0以及随机变量的状态值j，i0，i1，i2，i3….it-1，i1∈E。都代表

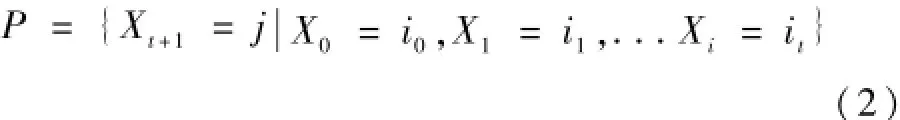
则表示｛x，t∈T｝为马尔科夫链。通过马尔科夫链的表达式可以看出，马尔科夫链表示的系统含义是t+s时刻变量的一个状态值只和前个t时刻的状态相关，而和t时刻以前的状态无任何关联。

传统的马尔科夫链未能考虑各个变量因子之间的权重系数，在收敛计算时存在收敛异常的情况，为此本文引入改进的马尔科夫链。改进的马尔科夫链主要是通过建立各个因子不同的转移概率权重，利用标准化的各因子的自相关系数作为转移概率权重，将变量的某一个时刻的状态转移概率进行加权，以加权后的概率作为变量在某个时刻的预测值。从而预测该变量标准化因子所处在的变量值。改进的马尔科夫链变量的径流预测的主要步骤：

（1）通过建立各个变量因子的不同等级的标准以及各因子变化转移的概率系数，采用标准方差法进行不同等级的标准化。通过这种方法来确定径流预测不同时刻的状态值。因为需要计算不同等级下的各因子的变化转移的权重系数，所以需要对各个因子的概率权重系数进行相关计算。

（2）各因子不同相关系数及标准。通过对各个影响因子进行相关系数的计算，相关系数计算公式为：

式中，xi表示的第i个时刻的变量状态值，在文中表示为径流值，x-表示为径流的平均值。

对各个变量因子进行标准化处理，标准化处理公式为：

式中，m代表的物理意义为模型预测计算的最大因子数。

（3）结合前面2个步骤中不同时刻的计算值作为初始的状态值，对应各个变量的转移概率加权权重系数，可以推算出下个时刻不同的状态变量值，其中K表示的模型计算时段的步长，本文选用年、月2个时间步长。

（4）将处在同一个时间变量的状态预测值和各个因子的权重进行叠加计算，可以表示某个变量在该状态下的概率预测值，表达式为：

该时刻的计算最大概率值表示预测时刻对应下的状态值。

（5）基于模糊数学的理论，通过各个状态变量不同权重系数可以得到各因子的权重矩阵wi，则得到年径流的预测值，表达式为：

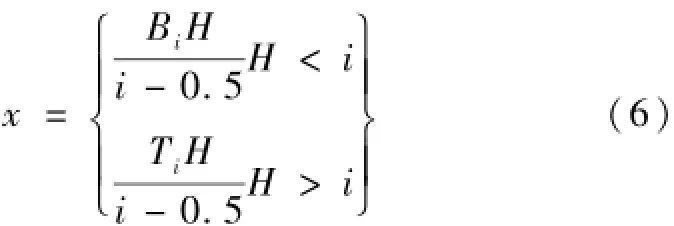
式中，T和B分别表示的变量状态的上下边界。

（6）结合改进的马尔科夫链的游历和方程稳定的特点，可以计算不同状态的变量概率值。

2 实例应用

2.1 数据说明

选用辽宁二道河子水文站1980～2010年经过还原的天然径流数据，运用改进前后的马尔科夫链进行径流预测，其中1980～2000年径流数据用于模型训练分析，2000～2010年径流数据用于模型预测，结合实测水文数据对比分析改进的马尔科夫链模型和传统马尔科夫链模型预测精度，模拟的时间尺度分为年尺度和月尺度。

2.2 模拟结果对比分析

2.2.1 年径流预测结果对比分析

基于改进的马尔科夫链和传统的马尔科夫链分别对辽宁二道河子水文站2000～2010年天然径流进行预测，并和水文站实测结果进行对比分析。模拟结果见表1和图1。

表1 改进的马尔科夫链模型模拟径流量年尺度预测对比成果

从表1中可以看出，改进的马尔科夫链预测的径流和实测的径流值误差5.6%～13.2%之间，相对误差的平均值为8.29%，而传统的马尔科夫链预测的径流值和实测的径流值相对误差在10.7%～18.1%之间，相对误差的平均值14.96%，可见改进的马尔科夫链提高了径流预测的精度。其次从图1中也可以看出，改进的马尔科夫链预测的年尺度径流值和实测的径流值的相关系数为0.8534，而传统的马尔科夫链预测的年尺度径流值和实测的径流值的相关系数为0.6806，可见在年尺度上改进的马尔科夫链预测的径流值和实测的径流值相关度更高。

2.2.2 月径流预测结果对比分析

由于径流在各个月份的值均不同，为此本文结合改进的马尔科夫链对月尺度的径流值进行预测，也和传统的马尔科夫链进行对比分析，结果见表2和图2。

表2 改进的马尔科夫链模拟径流月尺度预测对比成果

从表2中可以看出，改进的马尔科夫链预测的月尺度径流和实测的径流值相对误差在6.6%～13.2%之间，相对误差的平均值为11.2%，而传统的马尔科夫链预测的月尺度径流值和实测的径流值相对误差在14.2%～28.6%之间，相对误差的平均值20.2%，可见改进的马尔科夫链明显提高了月尺度径流预测的精度。其次从图2中也可以看出，改进的马尔科夫链预测的月尺度径流值和实测的径流值的相关系数为0.8477，而传统的马尔科夫链预测的年尺度径流值和实测的径流值的相关系数为0.6422，可见在月尺度上改进的马尔科夫链预测的径流值和实测的径流值相关度更高。

图2 改进的马尔科夫链模型径流预测月尺度精度对比

3 结语

本文通过引入加权系数，对传统马尔科夫链模型进行改进，并应用改进的马尔科夫链模型进行径流预测，研究得出以下结论：

（1）改进的马尔科夫链模型解决了传统马尔科夫链模型不能考虑各因子的权重的局限，改善模型计算收敛性。

（2）改进的马尔科夫链模型在径流预测精度上明显好于传统马尔科夫链模型，在年尺度径流模拟相关系数提高近0.17，月尺度径流模拟相关系数提高近0.21。

［1］张卫东.二维泥沙数学模型在唐河倒虹吸工程设计中的应用［J］.水利规划与设计，2010（03）：40-42.

［2］童晔，朱大伟.数值模拟在平原河网地区供水规划中的应用研究［J］.水利规划与设计，2015（01）：16-18.

［3］寇尔丹.基于M IKE21的异型堰模型分析［J］.水利技术监督，2015（03）：63-66+79.

［4］陈文熙.基于一维非恒定流数学模型的辽宁省引水隧洞糙率推求研究［J］.水利技术监督，2015（04）：35-38+41.

［5］崔东文.多隐层BP神经网络模型在径流预测中的应用［J］.水文，2013（01）：68-73.

［6］于国荣，夏自强.混沌时间序列支持向量机模型及其在径流预测中应用［J］.水科学进展，2008（01）：116-122.

［7］卫晓婧，熊立华，万民，等.融合马尔科夫链-蒙特卡洛算法的改进通用似然不确定性估计方法在流域水文模型中的应用［J］.水利学报，2009（04）：464-473+480.

［8］孙鹏，张强，涂新军，等.基于马尔科夫链模型的鄱阳湖流域水文气象干旱研究［J］.湖泊科学，2015（06）：1177-1186.

［9］孙鹏，张强，白云岗，等.基于马尔科夫模型的新疆水文气象干旱研究［J］.地理研究，2014（09）：1647-1657.

［10］李祥，王心源，李玉龙，等.基于灰色-马尔科夫预测模型的巢湖流域洪涝灾害预测研究［J］.水文，2006（04）：43-46+54.

P338

A

1008-1305（2017）01-0085-03

DO I:10.3969/j.issn.1008-1305.2017.01.026

2015-12-21

刘晓哲（1983年—），男，工程师。