滑坡堰塞湖溃坝影响因素数值模拟

李 杨

（抚顺市水利勘测设计研究院，辽宁抚顺113006）

滑坡堰塞湖溃坝影响因素数值模拟

李 杨

（抚顺市水利勘测设计研究院，辽宁抚顺113006）

文章对滑坡堰塞湖溃坝风险进行分析、监测和控制是滑坡灾害至关重要。通过Fluent软件构建溃坝洪水波模型，对滑坡堰塞湖溃坝影响因素进行模拟，并将结果与Martin标准实验做对比。研究结果表明：在不同溃决时间下，洪水流量变化图呈现显著的“先升后降”特征，然而洪水流量峰值出现时刻存在显著差异；溃决时间越少，溃坝对下游造成的破坏程度越大，影响范围也越宽广。

水利工程；滑坡灾害；堰塞湖；溃坝事故

在地震、泥石流或者大型工程建设后，山谷两侧岩石和土壤等可能出现滑坡，从而堵塞河道形成堰塞湖［1］。由于堰塞湖本身构造具有不稳定性，极易诱发次生灾害。比如，2008年汶川地震后，形成数百个堰塞湖，在余震、暴雨等地质或气象作用下，堰塞湖存在较高溃坝风险，对下游居民安全造成严重隐患。因此，有必要采取适当的方法、技术，对滑坡堰塞湖溃坝影响因素进行分析，以便制定科学、合理而具有可操作性的防范措施［2］。

本研究拟通过Fluent软件构建溃坝洪水波模型，对滑坡堰塞湖溃坝影响因素进行模拟，并将结果与Martin标准实验做对比。希望该研究能够起到三方面的作用。

第一，对溃坝危害程度作模拟，以便确定更加科学的防洪设计等级；

第二，对溃坝影响范围作模拟，以便一旦出现事故及时地对下游进行疏散；

第三，为溃坝事故灾后分析提供可资借鉴的方法和工具。

1 溃坝洪水波数学模型

1.1 模型构建

以Martin模型为参考，构建溃坝流动模型［3］。如图1所示，该模型包含水体（water）、压力出口边界（pressure out）以及固体壁面边界（wall）三个条件［14］。其中，水体高度、宽度的初始值分别为0.20m、0.10m。模型实践步长Δt=0.0005s，单元网格尺寸为Δx×Δy=4cm×4cm。

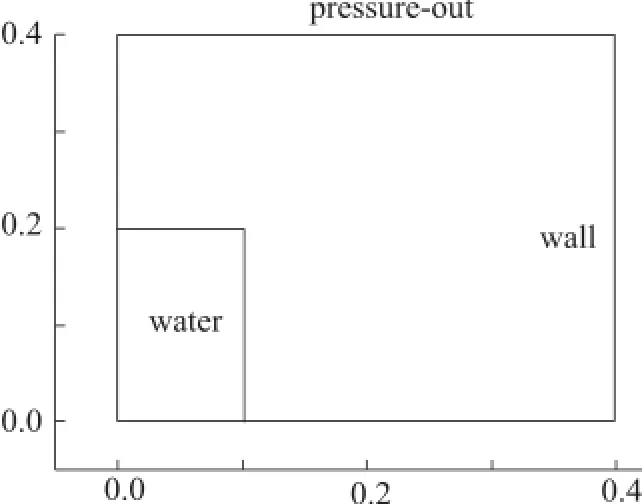
图1 溃坝洪水波模型

1.2 结果验证

为验证模型效果，本研究分别对t=0.1s、t= 0.15s、t=0.2s和t=0.3s时刻的溃坝洪水波进行计算。

结果表明，各个时刻下的洪水波始终处于压力出口边界、固体壁面边界内；流体前部质点速度随着前端压力的增加而提升，后部质点速度随着后端压力的降低而下降；模型能够对流体质点活动作准确表达，模型与溃坝洪水实际较为吻合。

在验证过程中，充分借鉴了Martin等人的研究成果，并严格依据如下公式对溃坝洪水波模拟值、溃坝标准实验值作对比［5-7］：

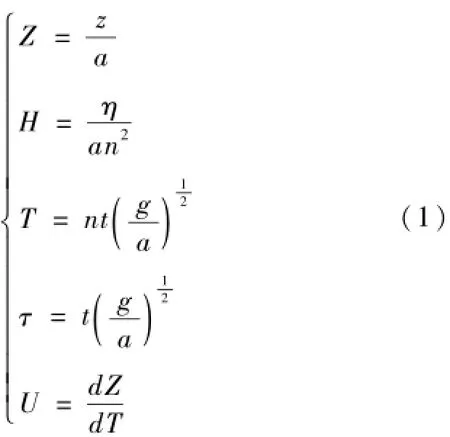
在水体高度H=0.20m、水体宽度a=0.10m、n2=2时，可求取标准化水波表达式。如图2所示，实线部分为Martin等人的标准实验结果，它与本实验的计算结果具有较为理想的一致性。

图2 时间-波前锋位置标准化关系

2 溃决模式对溃坝波的影响

不同溃决模式下，水体流速、前锋高度、剩余坝体高度等都会存在差异，因而会形成不同的溃坝波特征。可见，溃坝波与溃决模式之间存在紧密联系。如图3所示，对完全溃坝模式、1/2溃坝模式以及1/3溃坝模式下的流量变化情况进行进行对比。在x=0.10m处，随着溃坝时间推进，三种溃坝模式下洪水流量都呈“先增后降”特征；在同一时刻下，溃坝开口越大，洪水流量也越大。

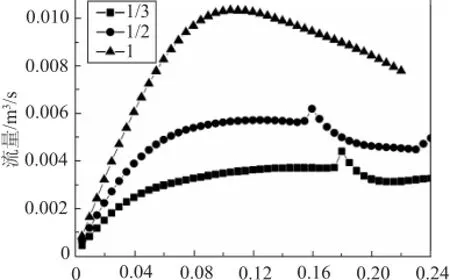
图3 时间-溃坝流量关系变化图

3 河道工况对溃坝波的影响

3.1 不同水深比溃坝波分析

为分析水深比对溃坝波所造成的影响，本研究共设置了0、0.10和0.45三个水深比。结果表明，对坝体上游而言，不同时刻下的波形特征较为一致，水深比对溃坝波无显著影响；对坝体下游而言，水深比越小，洪水峰值越多，溃坝波的推动速度也越快。

3.2 不同坡降比溃坝波分析

本研究中，在坝体下游共设置了0.10、0.20和0.50三个坡降比，并将初始水体高度、宽度以及河道长度分别设定为0.20m、0.20m和0.90m。如图4所示，为下游x=0.40m处的时间-流量走势图。由图4可知，三种坡降比下洪水流量都呈“先增后降”特征；在0.05s至0.45s之间的同一时刻下，坡降比越大，洪水流量也越大；其它时刻段，三种坡降比下的洪水流量十分一致。

图4 时间-流量变化曲线

图5 洪水前锋随时间到达的位置

如图5所示，随着时间推进，三种坡降比下的洪水前锋都向下游推动。在0.28s之前，三类洪水前锋所处位置几乎一致。0.28s以后，0.5坡降比下的洪水前锋推动速度最快，所处位置最靠前。可见，0.28s后同一时刻下洪水前锋位置与坡降比呈正比关系。

3.3 不同弯曲程度溃坝波分析

在研究河道弯曲度对溃坝波的影响时，构建正弦模型，并共设置了0.062、0.125、0.250和0.312四个弯曲度水平；同时，将河道水平长度、宽度和波幅分别设置为1.21单位、0.05单位和0.10单位。

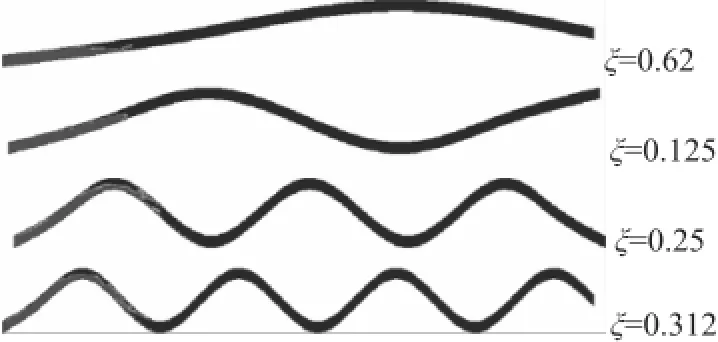
图6 不同弯曲度下自由面分布情况

如图6所示，在t=1.0s时刻，4种弯曲度下的自由面分布存在细微差异。其中，在弯曲度为0.062时，洪水自由面为0.251单位；当弯曲度为0.125时，洪水自由面为0.250单位；当弯曲度为0.250时，洪水自由面为0.249单位；当弯曲度为0.312时，洪水自由面为0.232单位。可见，弯曲度会在一定程度上降低自由面。另外，随着弯道增大，洪水在向前推进过程中会消耗更多能量，其推进速度会被逐渐降低。

4 溃决时间对溃坝波的影响

在研究坝体溃决时间对溃坝波的影响时，共设置了0.10s、0.20s和0.30s三个溃决时刻。在实验初始时，将水体高度、水体宽度以及水槽长度分别设置为0.20m、0.10m和0.40m。同时，将坝体设定位刚性结构，且其高度值为0.20m。

4.1 溃决时间对洪水流量的影响

如图7所示，在3种溃决时间下，洪水流量变化图呈现显著的“先升后降”特征。然而，三种溃决时间下的洪水流量峰值出现时刻存在显著差异。

当溃决时间为0.10 s时，溃口初始值最大，洪水流量在0.02s内达到0.005m3/s。随着时间推进，溃口越来越大，在0.14s时刻便出现水流峰。之后，洪水能量被大量消耗，流量快速下降。

当溃决时间为0.20 s时，溃口初始值较小，在0.14s时刻之前，洪水流量一直低于0.004m3/s。当洪水时间推进到0.14s后，流量跳跃性地上升至0.008m3/s。此后，流量快速增加，并在0.195s达到峰值后快速下降。

当溃决时间为0.30 s时，溃口初始值最小。随着时间推进，洪水流量逐步上升并在0.25s达到峰值。之后，洪水能量被大量消耗，流量逐步下降至平稳状态。

图7 溃决时间-洪水流量关系图

4.2 溃决时间对水面高程的影响

如图8所示，在t=0.30s时刻，溃决时间越短，洪水能够到达的位置就越远。当溃决时间为0.10s时，0.35m位置处水体高程超过0.02m；当溃决时间为0.20s时，0.35m位置处水体高程约为0.01m；当溃决时间为0.30s时，0.35m位置处已经不会受到洪水影响，且最近受影响位置为030m处。由图8可知，溃决时间越少，溃坝对下游造成的破坏程度越大，影响范围也越宽广。

图8 溃决时间对水面线高程的影响

5 结语

通过Fluent软件构建溃坝洪水波模型，对滑坡堰塞湖溃坝影响因素进行模拟，并将结果与Martin标准实验做对比。结果表明，本研究所构建模型具有较高合理性及适用性。研究得出如下几点结论。

（1）对坝体上游而言，不同时刻下波形特征较为一致，水深比对溃坝波无显著影响；对坝体下游而言，水深比越小，洪水峰值越多，溃坝波的推动速度也越快。

（2）0.10、0.20和0.50三个坡降比下，洪水流量都呈“先增后降”特征；在0.05s至0.45s之间的同一时刻下，坡降比越大，洪水流量也越大；0.28s后，同一时刻下洪水前锋位置与坡降比呈正比关系。

（3）弯曲度会在一定程度上降低自由面；随着弯道增大，洪水在向前推进过程中会消耗更多能量，其推进速度会被逐渐降低。

（4）在不同溃决时间下，洪水流量变化图呈现显著的“先升后降”特征，然而洪水流量峰值出现时刻存在显著差异。

（5）溃决时间越少，溃坝对下游造成的破坏程度越大，影响范围也越宽广。

［1］高大鹏.橡胶坝库区水面不连续问题解决方案设计优化［J］.水利规划与设计，2014（05）：61-62.

［2］王海丽.水库大坝溃坝事故洪水预测数值计算研究［J］.水利技术监督，2016（02）：56-57+72.

［3］喻少平.叶尔羌河下游河道演变及治理思路探究［J］.水利技术监督，2015（04）：9-11.

［4］徐娜娜，邢爱国.滑坡堰塞湖溃坝波影响因素分析［J］.人民黄河，2012，34（01）：83-85+88.

［5］党洁.地震诱发新疆乌吐劲堰塞湖形成过程的遥感研究［D］.新疆师范大学，2015.

［6］梁志山，牟萍，袁明道.广东省梅丰水电站A坝溃坝影响初步分析［J］.水利规划与设计，2013（08）：48-50.

［7］徐娜娜.大型滑坡涌浪及堰塞坝溃坝波数值模拟研究［D］.上海交通大学，2011.

P315.9

A

1008-1305（2017）01-0146-04

DO I:10.3969/j.issn.1008-1305.2017.01.044

2016-04-30

李 杨（1979年—），男，工程师。