基于速度障碍法和动态窗口法的无人水面艇动态避障
张洋洋,瞿栋,柯俊,李小毛
(上海大学机电工程与自动化学院,上海 200072)
基于速度障碍法和动态窗口法的无人水面艇动态避障
张洋洋,瞿栋,柯俊,李小毛
(上海大学机电工程与自动化学院,上海 200072)
速度障碍法是一种普遍应用在无人水面艇(unmanned surface vehicle,USV)上的动态避障方法,但传统的速度障碍法未考虑无人水面艇运动学性能与障碍物运动信息误差的影响,也未明确何时开始避障与结束避障.在速度障碍法的基础上,用椭圆表示无人水面艇与障碍物,给出一种求解椭圆切线的方法;将动态窗口法与速度障碍物法相结合,考虑无人水面艇的运动学性能,只使用无人水面艇在给定时间内能到达的速度和方向进行避障计算;通过比较碰撞时间与无人水面艇避开障碍物所需的时间来确定何时开始避障,并提出一种结束避障的判断方法;为了减小障碍物运动信息误差的影响,提出了一种虚拟障碍物方法.最后,通过仿真实验验证了该避障方法的可行性与有效性.
无人水面艇;动态避障;速度障碍;动态窗口;虚拟障碍物
无人水面艇(unmanned surface vehicle,USV)是一种轻型智能水面运载工具,具有体积小、造价低、速度快、机动性强等特点.近年来,随着控制、传感、无线通信技术的不断进步,无人水面艇得到了迅速发展.通过搭载不同的设备,无人水面艇可以应用在不同的领域,如环境监测、水质采样、海岸保护、海底测绘、军事等.
如果要保证无人水面艇能够在海洋中安全地航行,那么无人水面艇必须能够对航行过程中遇到的岛屿、暗礁、灯塔、浮标和航行的船只等其他障碍物进行自主避障.无人水面艇自主避障归类于平面移动机器人路径规划领域,经过国内外学者多年的研究,目前已经有很多成熟的算法用于移动机器人的路径规划.
Fox等[1]将路径规划分为两类:全局路径规划和局部路径规划.全局路径通常假设在完全已知环境信息的情况下,离线计算出一条从起点到终点的完全路径;但当不完全可知环境信息时全局路径规划就不能规划出安全的路径,且实时性不好,环境一旦改变就不能快速计算出新的路径.局部路径规划通过传感器获得的部分环境信息在线实时计算出可行路径.局部路径规划可分为两类:①当障碍物为静态时称为静态避障;②当障碍物为动态时称为动态避障,动态避障算法也可用于静态避障.动态避障算法比较有难度,因为通过移动机器人自身携带的传感器很难精确地获得动态障碍物的运动信息,无法对障碍物的运动趋势进行准确的预测.局部路径规划计算量小,实时性好,但由于不完全可知环境信息,因此容易陷入极小值点.根据全局路径与局部路径的特点,目前通常采用全局与局部相结合的多层避障结构.Campbell等[2]提出了一种混合的避障结构,即首先通过已知的环境信息(通常为地图),离线规划出一条从起点到目标点的可行路径,该路径应避开地图上已知的静态障碍物,机器人沿着该路径行驶,当在行驶过程中通过传感器检测到新的障碍物时,再通过传感器获得的障碍物的详细信息进行局部避障.Casalino等[3]提出了一种3层的避障结构,即在局部避障中又增加了一层反应式的避障结构,来应对障碍物运动信息不可知的避障场景.
目前,常用的全局路径规划算法主要有Dijkstra’s算法[4]、A∗算法[5]及其改进算法[6-9]、D∗算法[10]、进化算法[11-12]、神经网络算法[13]和快速扩展随机树算法[14-16]等.
目前,局部路径规划也有很多成熟的算法,文献[17-19]介绍了bug系列算法中的Tangent-Bug避障算法和不同bug算法的性能对比,bug系列算法中机器人主要有两种模式:朝目标点行走模式和绕障碍物行走模式.不同bug算法之间的主要区别在于在两种模式之间切换的条件不同,TangentBug避障算法在判断机器人陷入极小值点时切换到绕障碍物行走模式.文献[20-24]介绍了基于bug算法的改进算法及算法的实际应用.人工势场法[25-26]是一种虚拟力场法,即障碍物产生一个对机器人的斥力使得机器人与障碍物保持安全距离,目标点产生一个对机器人的引力,使得机器人驶向目标点,引力和斥力的合力决定着机器人的运动方向和运动速度.人工势场法计算量小,实时性好,但容易出现局部极小值点.文献[27]中通过使用一种带记忆功能的“沿边法”来解决极小值问题.Zohaib等[28]将文献[29]提出的FGM(follow the gap method)算法与bug算法相结合,提出了一种IFGM(intelligent FGM)避障算法,可用于在U形和H形障碍物环境中避障,可以解决由U形和H形障碍物引起的极小值问题.一般避障算法在算法层面上并不考虑机器人的运动学性能,故Fox等[1]和Brock等[30]考虑机器人的运动学约束,提出了一种动态窗口法,该方法只计算在给定的时间间隔内机器人能达到的速度,这些可达的速度构成一个速度空间(v,w)的集合,这个集合即为动态窗口,通过构建的目标函数,从动态窗口中选择出最优的可行速度.Seder等[31]通过结合D*算法与动态窗口并进行一些改进,提出了一种用于动态障碍物的动态窗口法,即将动态障碍物建模为移动的栅格,通过预测障碍物与机器人的碰撞点构建一个虚拟的障碍物,机器人应该避过该虚拟障碍物.Tang等[32]在动态窗口的基础上提出了一种OAABHW(obstacle avoidance algorithm based on heading window)避障算法,该算法将动态窗口转化为艏向和速度窗口,构建两个函数分别用来选择避障速度和避障方向.Zhang等[33]基于文献[32],结合Sarsa在策略强化学习算法,提出了一种新颖的适用于无人水面艇的自适应避障算法,该算法基于Sarsa自适应学习模块处理海风和涌流的影响,通过对航向角进行补偿来减小海风和涌流的干扰,提高无人水面艇的避障性能.在Casalino等[3]提出的3层避障结构的第2层中,障碍物被定义为一个矩形边界框,通过假设无人水面艇与障碍物的速度恒定,分别计算出无人水面艇与矩形边界框4个顶点的碰撞位置,将无人水面艇位置点、目标点与这些碰撞位置点连接,构成多条路径,并通过A*算法计算出最优路径.Simetti等[34]对文献[3]中的算法进行了一些改进,即在矩形边界框的外部又增加了一个支持边界框来减小误差的干扰,同时采用了保持避障方向策略,一旦计算出一个初始避障角度,如果没有出现新的危险影响无人水面艇,则无人水面艇一直沿着这个避障方向运动,直到认为避开障碍物为止.Wu等[35]提出了一种基于方向权重的无人水面艇动态避障算法,通过相对速度计算出与障碍物最近接近点(closest point of approach,CPA)的距离(distance of CPA, DCPA)、方位,以及到达该点的时间(time to CPA,TCPA).将不同的方向赋予权重,其中无人水面艇当前航向方向权重最大,其两边方向的权重逐渐减小;障碍物方向与CPA方向的权重最小,CPA方向两边方向的权重逐渐增大;当采用海事规则时,根据海事规则不可行的方向权重最小.综合计算这些权重,求出权重最大的方向作为避障的方向.Chakravarthy等[36]对速度进行切向和径向分解,预测点与点之间的碰撞,然后推广到两个不规则目标之间的碰撞,提出了一种碰撞锥的避障方法.Chakravarthy等[37]通过将障碍物建模为2次曲面,提出了一种可用于3维空间的碰撞锥动态避障方法.另外,速度障碍法是目前广泛应用在无人水面艇上的动态避障算法,由Fiorini[38]提出,该算法对每个障碍物在速度空间上构建一个锥形区域,只要速度矢量落入该区域即认定会发生碰撞,从非锥形区域中选择一个最优的速度矢量进行避障. Kuwata等[39]将速度障碍法与海事规则相结合,用于无人水面艇的动态避障,并通过相对速度计算出无人水面艇与障碍物最近接近点的距离和到达该点的时间.当DCPA和TCPA都满足给定的约束条件时才认定会发生碰撞,并通过构建一个代价函数,从可行速度空间里选择一个能使代价函数最小的速度矢量作为避障的速度矢量.文献[40-41]中都将海事规则与避障算法相结合,用于无人水面艇避障.
上述文献中提出的局部避障算法基本都假设障碍物为圆形,且完全已知障碍物的位置、运动信息.然而,无人水面艇在海上航行时遇到的障碍物大部分为船只,而船只具有长宽比大的特点,圆形不能形象地表示船只,会将船只在宽度方向放大很多;而船只的形状与椭圆很相似,因此使用椭圆可以较好地表示出船只障碍物.故本工作在文献[38]速度障碍法的基础上,使用椭圆表示障碍物,并结合动态窗口法考虑无人水面艇的运动学约束,改进速度障碍法用于无人水面艇的静态、动态避障.在无人水面艇实际航行时,通过无人水面艇自身携带的传感器很难精确获得障碍物的运动信息,为此本工作通过增加虚拟障碍物来减小障碍物运动信息误差的影响.
1 基于椭圆的速度障碍法
1.1 速度障碍原理
文献[38]中详细介绍了速度障碍法的基本原理,本工作对速度障碍法进行简单回顾.分别用P∈R2和V∈R2表示在t时刻一个机器人在2维平面中的位置和速度矢量.在以下的分析中将障碍物和无人水面艇的形状都简化为椭圆.
如图1所示,绿色椭圆A为无人水面艇,PA为无人水面艇的位置矢量,红色椭圆B为“膨化”后的障碍物,即将无人水面艇的尺寸叠加到障碍物的尺寸上,为了简化分析并保证无人水面艇的安全,将无人水面艇椭圆的半长轴分别叠加到障碍物椭圆的半长轴和半短轴上,这样就将无人水面艇简化为一个质点;PB表示障碍物的位置矢量.图1中绿色箭头VA、VBA分别为无人水面艇的速度矢量、无人水面艇相对于障碍物的速度矢量,红色箭头VB为障碍物的速度矢量,VBA通过式(1)求得

定义从一点P沿V方向发出的射线为

当求得相对速度VBA后,通过相对速度可以将障碍物B看作静止.假设无人水面艇速度VA与障碍物速度VB保持不变,则当从PA点发出沿VBA方向的射线λBA与障碍物B相交,即射线λBA落在障碍物B相对于无人水面艇A的两条切线夹角内时,可认为无人水面艇会在将来某一时刻t1与障碍物发生碰撞.定义使A会与B碰撞的相对速度VBA的集合为RCCAB(relative collision cone),RCCAB称为在A与B的相对速度空间里的相对碰撞区域:式中,RCCAB即为障碍物B相对于无人水面艇A的左右切线λL,λR中间的灰色区域.
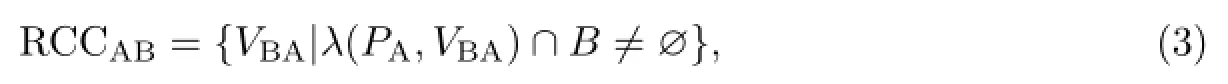
相对碰撞区域RCC定义在无人水面艇A与障碍物B的相对速度空间里,但是如果存在多个障碍物时,则需要将每个障碍物的RCC转换到统一的速度空间里表述.定义在无人水面艇的绝对速度空间里,会与障碍物B发生碰撞的无人水面艇速度VA的集合为VOAB(velocity obstacle),称VOAB为速度障碍:

式(4)等价表述为
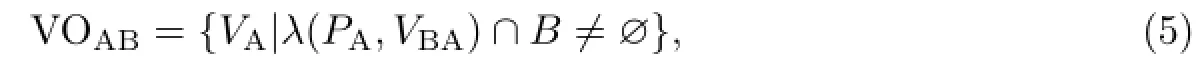
式(4)中,⊕为闵可夫斯基矢量和运算.如图1所示,VOAB即为图中的蓝色阴影区域,相当于将RCCAB沿VB方向平移,当速度矢量VA的箭头落在该蓝色区域内时,无人水面艇A会与障碍物B发生碰撞.
当存在多个障碍物时,求出所有障碍物的VO集合的并集后得到总的VO集合:

对于无人水面艇A,非VO集合中的速度矢量不会与障碍物发生碰撞,即在给定的时间内将无人水面艇当前的速度矢量VA调整到非VO区域无人水面艇即可避开障碍物.
1.2 计算椭圆切线
在速度障碍法中,如果要判断无人水面艇是否会与障碍物发生碰撞,则必须要求出障碍物相对于无人水面艇的两条切线.为了方便求出椭圆障碍物的切线,本工作建立了无人水面艇船体和障碍物坐标系,在障碍物坐标系中用椭圆标准方程表示椭圆障碍物.首先将无人水面艇位置转换到障碍物坐标系中,即在障碍物坐标系中求得两条切线的切点,再将切点转换到船体坐标系,这样便求出障碍物相对于无人水面艇的两条切线.
如图2所示,xOy为无人水面艇船体坐标系,x′O′y′为障碍物坐标系;红色椭圆为障碍物,绿色椭圆为无人水面艇,已简化为质点;点O为无人水面艇中心;O′为障碍物中心.无人水面艇在船体坐标系中的坐标为USVboat=[0,0]T,则无人水面艇在障碍物坐标系中的坐标USVobs=[m,n]T为

式中,C为障碍物中心点在船体坐标系中的坐标,R为障碍物坐标系相对于船体坐标系的旋转矩阵

当求得无人水面艇在障碍物坐标系中的坐标后,在障碍物坐标系中联立标准椭圆方程与椭圆切线方程:

即可求得在障碍物坐标系中切点的坐标(xT,yT)(如图2中的T1obs,T2obs).通过


图2 椭圆切线Fig.2 Ellipse tangents
计算切点T1obs,T2obs在船体坐标系中的坐标(如图2中的T1boat,T2boat),求出两个切点后即可计算出在船体坐标系中障碍物相对于无人水面艇的两条切线.
2 避障算法
根据无人水面艇与障碍物之间的距离,将无人水面艇周围的区域分为3个:安全、常规避障和紧急避障区域(见图3),其中可认定在安全区域内的障碍物安全,不会对无人水面艇造成威胁;同时由于安全区域范围大,可能会存在大量障碍物,故为了减小计算量,对安全区域内的障碍物不进行避障计算处理.在紧急避障区域内的障碍物对无人水面艇会产生严重威胁,为此无人水面艇需要采取紧急措施.本工作主要介绍无人水面艇在常规避障区域内的避障.
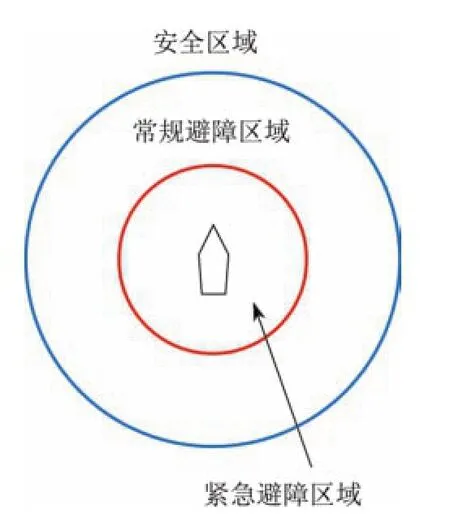
图3 避障区域Fig.3 Avoidance zones
无人水面艇在执行任务时,通过轨迹跟踪算法规划速度和方向,保证无人水面艇能沿着全局路径规划计算出的航迹线行驶,因此本算法中无人水面艇采用Breivik等[42-43]提出的视线制导(line of sight,LOS)轨迹跟踪算法,其基本思想就是在规划的轨迹线上选择一个虚拟的目标点,无人水面艇沿着该目标点行驶即可回归到航迹线上.
当无人水面艇将与障碍物发生碰撞时,本算法能根据无人水面艇避开障碍物所需时间来判断何时开始避障.开始避障后通过动态窗口法与速度障碍法计算避障速度与方向,并通过增加虚拟障碍物来减少障碍物运动信息误差带来的影响;当满足结束避障条件时,无人水面艇结束避障.图4为从开始避障到结束避障的流程.
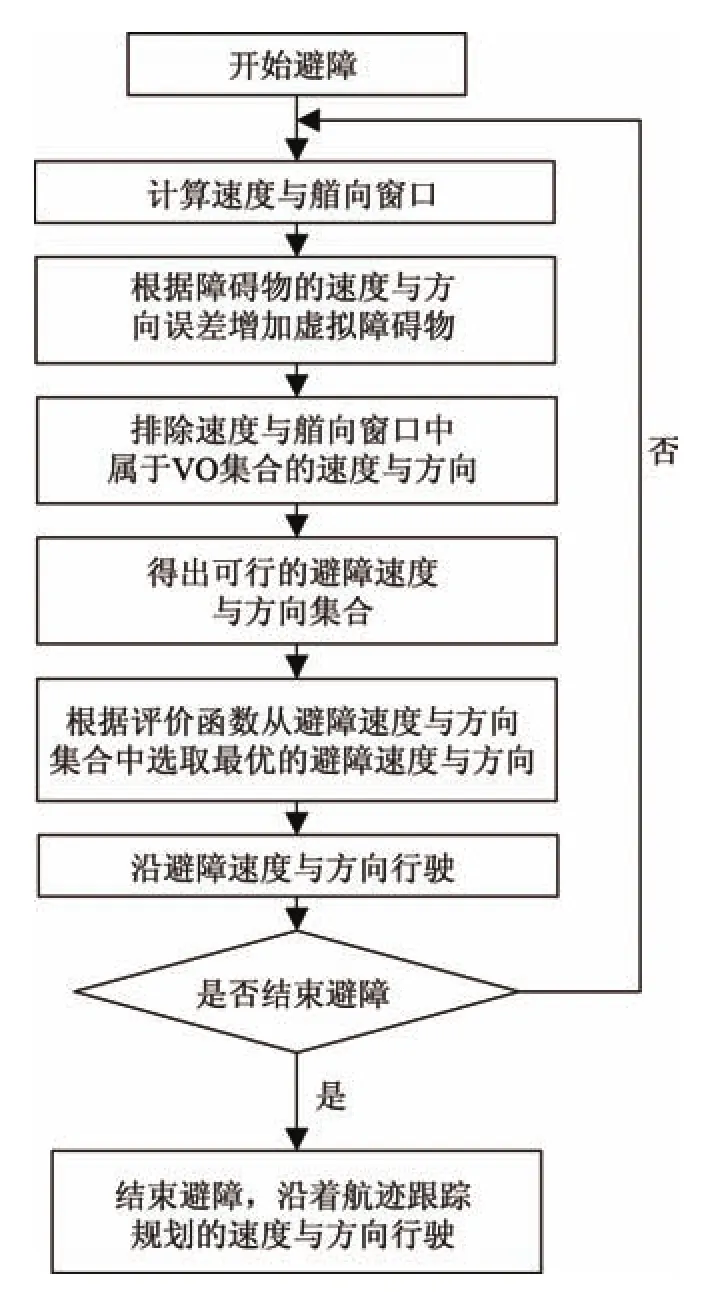
图4 避障流程Fig.4 Avoidance fowchart
2.1 基于动态窗口的速度障碍法
通过速度障碍法计算出会碰撞的VO集合后,非VO集合中的数据都为无人水面艇可选的避障速度矢量.然而,由于无人水面艇动力学性能的约束,无人水面艇在给定的时间内速度和方向不会改变很大,因此非VO集合内的很多速度矢量对于无人水面艇来说是不可及的,故不需要对这些速度矢量进行计算.
动态窗口法考虑了无人水面艇的运动学性能[1],只计算无人水面艇在给定时间窗口∆t内能达到的移动速度,即速度窗口

和角速度,即角速度窗口
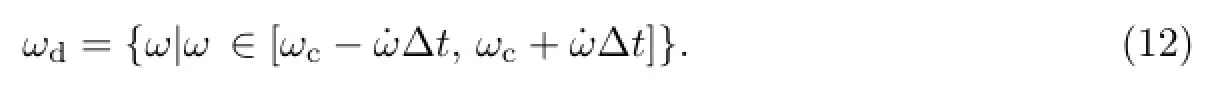
式(11)中,vc为无人水面艇当前的移动速度,˙v为无人水面艇的加速度;式(12)中,ω为无人水面艇当前的角速度,˙ω为无人水面艇的角加速度.通过继续对式(12)进行计算,可以求出无人水面艇在∆t内艏向可以转到的角度,即艏向窗口[32]

式中,θh为无人水面艇当前的艏向.
通过式(11),(13)即可确定无人水面艇在给定∆t内可以达到的速度大小vd和方向θd,但vd和θd集合中的元素都是连续的,不利于实际工程中的计算.为此本算法在实施过程中将vd速度窗口和θd艏向窗口离散化,即将vd离散为M个速度,θd离散为N个艏向,离散后的一个速度vi和一个艏向θi组成一个速度矢量(vi,θi),那么共有M×N个速度矢量.将这些无人水面艇在∆t时间内可达到的离散的速度矢量组成的集合称为RV(reachable velocity)(见图5(a)).RV集合中满足式(5)的速度矢量会与障碍物发生碰撞,从RV集合中排除会碰撞的速度矢量即可得到无人水面艇在∆t时间内可达到的、安全的速度矢量集合,称为RAV (reachable avoidance velocity)(见图5(b)):
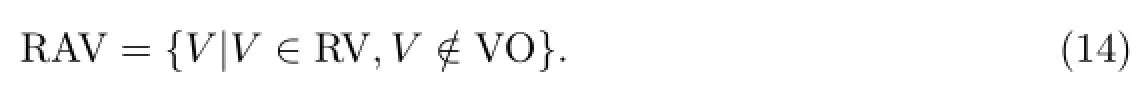
图5中,红色区域为VO区域,RV与VO相交的部分即为会发生碰撞的速度矢量,RAV部分为安全的速度矢量.

图5 RV与RAV速度Fig.5 RV and RAV velocity
求出RAV集合后,需要在RAV集合中选出最优的速度矢量进行避障.根据不同的任务有不同的选取准则,本算法中采用如下评价函数来选取,
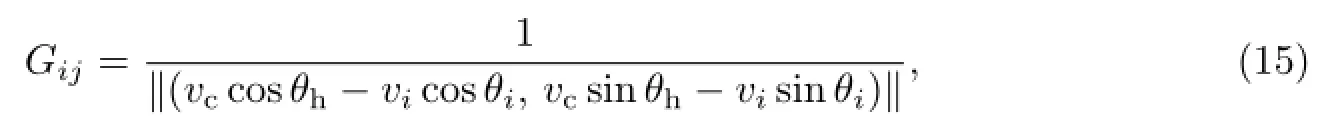
式中:vc为无人水面艇当前的速度;θh为无人水面艇当前的艏向;(vi,θi)为RAV集合中的某一速度矢量,将能使Gij最大的(vi,θi)作为无人水面艇避障的速度矢量.一旦选择了一个避障速度矢量,无人水面艇会一直沿着这个速度矢量行驶,直到出现新的危险或避开障碍物时才以新的速度矢量行驶.
2.2 开始与结束避障
在判断无人水面艇是否会与障碍物发生碰撞时,需要计算何时开始避障,一旦开始避障后就需要判断何时结束避障.本算法中采用两个条件明确开始避障和结束避障时间.
2.2.1 开始避障
当判断无人水面艇是否会与障碍物发生碰撞时,在碰撞时刻无人水面艇与障碍物之间的距离最小,各自的位置称为CPA,无人水面艇到达其CPA点所需的时间称为tCPA.如图6所示,红色与绿色实线椭圆分别为障碍物与无人水面艇在当前t0时刻的位置,Vobs与VUSV分别为障碍物与无人水面艇在t0时刻的速度矢量,红色与绿色虚线椭圆分别为障碍物与无人水面艇在tCPA时刻的位置,CPAobs点与CPAUSV点分别为在tCPA时障碍物与无人水面艇中心点的位置:


图6 距离最小点和开始避障点Fig.6 Close point approach and start avoidance point
假设保持无人水面艇速度大小不变,即可以恒定的角加速度转弯.图6中,无人水面艇以恒定速度和方向驶向CPAUSV点的过程中,在某点B以恒定角加速度左转弯,恰好沿曲线轨迹B—PL与障碍物相切于PL点.无人水面艇从B点行驶到PL点所需的时间为tL,则无人水面艇在tCPA=tL时刻开始左转避障,刚好会与障碍物相切于PL点:式中:(x,y),(xB,yB)分别为PL点、B点在障碍物坐标系中的坐标;v,θ0,ω0,α分别为无人水面艇当前速度、艏向、角速度和角加速度;PLC1+PLC2为在障碍物坐标系中PL点到椭圆两焦点的距离和;a为椭圆半长轴.

同理,无人水面艇在某点A以恒定角加速度右转弯,恰好沿曲线轨迹A—PR与障碍物相切于PR点.无人水面艇从A点行驶到PR点所需的时间为tR,则无人水面艇在tCPA=tR时刻开始右转避障,刚好会与障碍物相切于PR点.
定义开始避障时间为tavoid,则

式中,k为大于1的系数,保证无人水面艇的安全且转弯平缓.无人水面艇在tCPA=tavoid时开始避障,可以安全平缓地避开障碍物.
2.2.2结束避障
当无人水面艇开始避障后需要判断何时结束避障,本算法中无人水面艇执行任务时需要沿规划的航迹行驶到终点,故只要无人水面艇能安全地沿轨迹跟踪规划的速度与方向行驶,且安全地沿目标点方向行驶即可结束避障,也就是说无人水面艇在避障过程中满足

即可结束避障.式(19)中,VLOS为轨迹跟踪规划的速度矢量,Vdest为无人水面艇以当前速度大小沿目标点方向运动时的速度矢量.
2.3 虚拟障碍物
速度障碍法设定完全已知障碍物的运动信息,而在实际的航行过程中,无人水面艇通过自身携带的雷达、视觉、激光等传感器而获得的障碍物的运动信息会有误差,利用有误差的信息进行避障可能会引起无人水面艇与障碍物碰撞,故需要考虑障碍物运动信息的误差.
假设通过传感器获得的障碍物的速度矢量为Vt,障碍物速度矢量误差集合为VE,则障碍物实际可能的速度矢量集合

假设VP集合中的每个元素都为一个虚拟障碍物的速度矢量,虚拟障碍物的位置、尺寸与原障碍物相同,则虚拟障碍物的速度矢量为

求出一个障碍物及与其关联的每个虚拟障碍物的VO集合,求这些集合的并集,即为一个障碍物最终的VO集合,该集合考虑了障碍物运动信息的误差.
3 仿真实验
为了验证本算法的避障性能,在Matlab环境下分别对单个和多个动态障碍物场景进行仿真分析.
3.1 单个动态障碍物场景
图7为无人水面艇与单个动态障碍物相遇时的场景.图中绿色直线为规划的无人水面艇的航迹线,红色椭圆为障碍物以速度3.5 m/s、相对于正北方向90°运动,蓝色五边形为无人水面艇以速度5 m/s、沿正北方向运动.
图7中,假设障碍物的速度与运动方向恒定.但是,在实际场景中障碍物的速度与运动方向通过传感器获得,往往会有很大的误差.为了模拟传感器的这些误差,对障碍物的速度与运动方向增加干扰,即无人水面艇获得的是增加干扰后的障碍物的速度与运动方向.图8为障碍物的实际速度、运动方向与无人水面艇获得的障碍物的速度、运动方向.
图9(a)为采用虚拟障碍物时的避障过程,其中蓝色为无人水面艇轨迹,红色为障碍物轨迹,无人水面艇从障碍物后方成功避开障碍物.图9(b)为未采用虚拟障碍物方法时的避障过程,由于障碍物运动信息误差的影响,无人水面艇与障碍物碰撞.

图7 单个动态障碍物场景Fig.7 Single dynamic obstacle scene

图8 障碍物速度与运动方向Fig.8 Speeds and courses of obstacle

图9 避障过程Fig.9 Processes of avoidance
图10为在相同场景下采用与未采用虚拟障碍物时无人水面艇输出的避障方向,其中在0~15 s期间为避障过程.可以看出,未采用虚拟障碍物时无人水面艇输出的避障方向抖动严重,而采用虚拟障碍物时无人水面艇输出的避障方向稳定.
图11为在相同场景下采用与未采用虚拟障碍物时无人水面艇与障碍物的距离,可见采用虚拟障碍物时最近距离为23 m.由于无人水面艇船长为10 m,速度为5 m/s,该最小距离可以保证无人水面艇的安全;未采用虚拟障碍物时最近距离为9 m,无人水面艇与障碍物碰撞.

图10 避障输出方向Fig.10 Output courses of avoidance

图11 无人水面艇与障碍物的距离Fig.11 Distances between USV and obstacle
3.2 多个动态障碍物场景
在多个障碍物场景下,同样对每个障碍物的速度与运动方向增加了干扰.图12为存在2个动态障碍物时采用虚拟障碍物方法时的避障过程,可以看出无人水面艇正常避过2个动态障碍物.图13(a)为在相同场景下,未采用虚拟障碍物方法时无人水面艇与障碍物1发生碰撞,而图13(b)为未采用虚拟障碍物方法时无人水面艇成功避过障碍物2.

图12 采用虚拟障碍物时多障碍物避障过程Fig.12 Process of avoidance with multiple obstacles using virtual obstacles

图13 未采用虚拟障碍物时多障碍物避障过程Fig.13 Processs of avoidance with multiple obstacles without virtual obstacles
图14为在避障过程中无人水面艇输出的避障方向,图中0~15 s为无人水面艇躲避障碍物1的避障过程,30~45 s为无人水面艇躲避障碍物2的过程.采用虚拟障碍物方法时,无人水面艇在躲避2个障碍物过程中避障输出方向稳定.未采用虚拟障碍物方法时,无人水面艇在躲避障碍物1的过程中避障方向抖动严重,且与障碍物1发生碰撞;在躲避障碍物2的过程中,虽然无人水面艇成功避开障碍物,但输出的避障方向仍然抖动严重.

图14 输出的避障方向Fig.14 Output courses of avoidances
图15(a)为无人水面艇在行驶过程中采用与未采用虚拟障碍物法时与障碍物1的距离,其中采用虚拟障碍物时无人水面艇距离障碍物的最小距离为20 m,而未采用虚拟障碍物时无人水面艇与障碍物的最小距离为8 m;图15(b)为无人水面艇行驶过程中无人水面艇和障碍物2的距离,其中采用虚拟障碍物时无人水面艇距离障碍物的最小距离为18 m,而未采用虚拟障碍物时无人水面艇距离障碍物的最小距离为17 m.

图15 多障碍物时无人水面艇与障碍物的距离Fig.15 Distances between USV and obstacles with multiple obstacles
4 结束语
本工作改进了速度障碍法并用于无人水面艇动态避障,用椭圆表示无人水面艇和障碍物,考虑无人水面艇的运动学性能,只将无人水面艇在给定时间内能到达的速度和方向用于速度障碍法计算.另外,通过比较碰撞与避障所需时间来确定何时开始避障,当回归航迹与沿目标点运动都安全时可结束避障,并且使用虚拟障碍物来减小障碍物运动信息误差对避障过程的影响.通过仿真实验验证了本避障方法的效果.
本方法并未采用海事规则,即当无人水面艇的最大速度小于障碍物的速度时,如果无人水面艇选择从动态障碍物前方进行避障则会有碰撞危险,因此采用海事规则的动态避障可以更好地保证无人水面艇的安全.
[1]FOX D,BuRGARD W,THRuN S.The dynamic window approach to collision avoidance[J].IEEE Robotics&Automation Magazine,1997,4(1):23-33.
[2]CAMPBELL S,NAEEM W,IRWIN G W.A review on improving the autonomy of unmanned surface vehicles through intelligent collision avoidance manoeuvres[J].Annual Reviews in Control,2012, 36(2):267-283.
[3]CAsALINO G,TuRETTA A,SIMETTI E.A three-layered architecture for real time path planning and obstacle avoidance for surveillance USVs operating in harbour felds[C]//Oceans.2009: 1-8.
[4]DIJKsTRA E W.A note on two problems in connexion with graphs[J].Numerische Mathematik, 1959,1(1):269-271.
[5]HART P E,NILssON N J,RAPHAEL B.A formal basis for the heuristic determination of minimum cost paths[J].IEEE Transactions on Systems Science and Cybernetics,1968,4(2):100-107.
[6]KIM H,KIM D,SHIN J U,et al.Angular rate-constrained path planning algorithm for unmanned surface vehicles[J].Ocean Engineering,2014,84:37-44.
[7]KOENIG S,LIKHACHEV M,FuRCY D.Lifelong planning A*[J].Artifcial Intelligence,2004, 155(1):93-146.
[8]LIKHACHEV M,FERGusON D I,GORDON G J,et al.Anytime dynamic A*:an anytime,replanning algorithm[C]//Fifteenth International Conference on Automated Planning and Scheduling. 2005:262-271.
[9]LIKHACHEV M,KOENIG S.A generalized framework for lifelong planning A*search[C]//Fifteenth International Conference on Automated Planning and Scheduling.2005:99-108.
[10]STENTZ A.The focussed D*algorithm for real-time replanning[C]//International Joint Conference on Artifcial Intelligence.2000:3310-3317.
[11]BOTEA A,M¨uLER M,SCHAEFFER J.Near optimal hierarchical path-fnding[J].Journal of Game Development,2004,1(7):7-28.
[12]LEIGH R,LOuIs S J,MILEs C.Using a genetic algorithm to explore A*-like pathfnding algorithms[C]//IEEE Symposium on Computational Intelligence and Games.2007:72-79.
[13]YANG S X,LuO C.A neural network approach to complete coverage path planning[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B(Cybernetics),2004,34(1):718-724.
[14]MELCHIOR N A,SIMMONs R.Particle RRT for path planning with uncertainty[C]//IEEE International Conference on Robotics and Automation.2007:1617-1624.
[15]Hsu D,KINDEL R,LATOMBE J C,et al.Randomized kinodynamic motion planning with moving obstacles[J].International Journal of Robotics Research,2002,21(3):233-255.
[16]RODRIGuEZ,TANG X,LIEN J M,et al.An obstacle-based rapidly-exploring random tree[C]// IEEE International Conference on Robotics and Automation.2006:895-900.
[17]KAMON I,RIVLIN E,RIMON E.A new range-sensor based globally convergent navigation algorithm for mobile robots[C]//IEEE International Conference on Robotics&Automation.1995: 429-435.
[18]NG J,BR¨ANL T.Performance comparison of bug navigation algorithms[J].Journal of Intelligent and Robotic Systems,2007,50(1):73-84.
[19]KAMON I,RIMON E,RIVLIN E.TangentBug:a range-sensor-based navigation algorithm[J]. International Journal of Robotics Research,1998,17(9):934-953.
[20]MARAVALL D,LOPE J D,FuENTEs J P.Visual bug algorithm for simultaneous robot homing and obstacle avoidance using visual topological maps in an unmanned ground vehicle[M].New York:Springer International Publishing,2015:301-310.
[21]ZOHAIB M,PAsHA S M,JAVAID N,et al.Intelligent bug algorithm(IBA):a novel strategy to navigate mobile robots autonomously[C]//Springers International Multi Topic Conference. 2013.
[22]HAsHMI U,AFsHAN F,RAFIQ M.Performance analysis of diferent optimal path planning bug algorithms on a client server based mobile surveillance UGV[C]//International Conference on Intelligent Systems Modelling&Simulation.2013:30-35.
[23]BuNIYAMIN N,WAN N W,SARIFF N,et al.A simple local path planning algorithm for autonomous mobile robots[J].International Journal of Systems Applications,Engineering& Development,2011,5(2):151-159.
[24]MOHAMED E F,ELMETWALLY K,HANAFY A.An improved Tangent Bug method integrated with artifcial potential feld for multi-robot path planning[C]//International Symposium on Innovations in Intelligent Systems and Applications.2011:555-559.
[25]KHATIB M,CHATILA R.An extended potential feld approach for mobile robot sensor-based motions[C]//Intelligent Autonomous Systems.1995:490-496.
[26]KHATIB O.Real-time obstacle avoidance for manipulators and mobile robots[J].International Journal of Robotics Research,1986,5(1):90-98.
[27]HuANG Y,Hu H,LIu X.Obstacles avoidance of artifcial potential feld method with memory function in complex environment[C]//Intelligent Control and Automation.2010:6414-6418.
[28]ZOHAIB M,PAsHA S M,JAVAID N,et al.An improved algorithm for collision avoidance in environments having U and H shaped obstacles[J].Studies in Informatics&Control,2014, 23(1):97-106.
[29]SEZER V,GOKAsAN M.A novel obstacle avoidance algorithm:“follow the gap method”[J]. Robotics&Autonomous Systems,2012,60(9):1123-1134.
[30]BROCK O,KHATIB O.High-speed navigation using the global dynamic window approach[C]// IEEE International Conference on Robotics and Automation.1999:341-346.
[31]SEDER M,PETROVIC I.Dynamic window based approach to mobile robot motion control in the presence of moving obstacles[C]//IEEE International Conference on Robotics and Automation. 2007:1986-1991.
[32]TANG P,ZHANG R,LIu D,et al.Research on near-feld obstacle avoidance for unmanned surface vehicle based on heading window[C]//24th Chinese Control and Decision Conference.2012: 1262-1267.
[33]ZHANG R,TANG P,Su Y,et al.An adaptive obstacle avoidance algorithm for unmanned surface vehicle in complicated marine environments[J].IEEE/CAA Journal of Automatica Sinica,2014, 1(4):385-396.
[34]SIMETTI E,TORELLI S,CAsALINO G,et al.Experimental results on obstacle avoidance for high speed unmanned surface vehicles[C]//Oceans.2014:1-6.
[35]Wu G,SHI D,GuO J.Deliberative collision avoidance for unmanned surface vehicle based on the directional weight[J].Journal of Shanghai Jiaotong University(Science),2016,21(3):307-312. [36]CHAKRAVARTHY A,GHOsE D.Obstacle avoidance in a dynamic environment:a collision cone approach[J].Systems&Humans,1998,28(5):562-574.
[37]CHAKRAVARTHY A,GHOsE D.Collision cones for quadric surfaces[J].IEEE Transactions on Robotics,2011,27(6):1159-1166.
[38]FIORINI P.Motion planning in dynamic environments using velocity obstacles[J].International Journal of Robotics Research,1998,17(7):760-772.
[39]KuWATA Y,WOLF M T,ZARZHITsKY D,et al.Safe maritime autonomous navigation with colregs,using velocity obstacles[J].IEEE Journal of Oceanic Engineering,2014,39(1):110-119. [40]JOHANsEN T A,PEREZ T,CRIsTOFARO A.Ship collision avoidance and colregs compliance using simulation-based control behavior selection with predictive hazard assessment[J].IEEE Transactions on Intelligent Transportation Systems,2016,17:1-16.
[41]NAEEM W,IRWIN G W,YANG A.COLREGs-based collision avoidance strategies for unmanned surface vehicles[J].Mechatronics,2012,22(6):669-678.
[42]BREIVIK M,HOVsTEIN V,FOssEN T.Straight-line target tracking for unmanned surface vehicles[J].Modeling Identifcation and Control,2008,29(4):131-149.
[43]BREIVIK M,FOssEN T I.Guidance laws for planar motion control[C]//IEEE Conference on Decision and Control.2008:570-577.
Dynamic obstacle avoidance for USV based on velocity obstacle and dynamic window method
ZHANG Yangyang,QU Dong,KE Jun,LI Xiaomao
(School of Mechatronic Engineering and Automation,Shanghai University,Shanghai 200072,China)
Velocity obstacle is a dynamic obstacle avoidance algorithm widely used on an unmanned surface vehicle(USV).However,traditional velocity obstacle does not consider the efect of USV’s kinematics and obstacle’s motion information error,and does not know when to start and terminate avoidance.Based on velocity obstacle,USV and obstacle are represented by an ellipse.A method for solving ellipse tangent is proposed.Considering the kinematics performance of USV,a dynamic window method and velocity obstacle are combined.Only the speed and course that the USV can reach in a given time are used in calculation.By comparing the collision time and the time required for the USV to fnish avoidance to determine when to start avoidance,a method to terminate obstacle avoidance is proposed.A virtual obstacle method is then proposed to reduce infuence of obstacle’s motion information error.Feasibility and efectiveness of the method are verifed by simulation.
unmanned surface vehicle(USV);dynamic avoidance;velocity obstacle; dynamic window;virtual obstacle
TP 242
A
1007-2861(2017)01-0001-16
10.3969/j.issn.1007-2861.2016.07.021
2017-01-07
国家自然科学基金资助项目(61673254);上海市自然科学基金资助项目(13ZR1454300);上海市科委能力建设资助项目(14500500400)
李小毛(1981—),男,研究员,研究方向为图像处理、雷达数据处理、无人艇环境感知、导航和控制及其总体技术.E-mail:lixiaomao@shu.edu.cn

