6R机器人工作空间奇异点的可视化研究
符 晓, 谭月胜
(北京林业大学工学院,北京 100083)
研究与设计
6R机器人工作空间奇异点的可视化研究
符 晓, 谭月胜
(北京林业大学工学院,北京 100083)
分析机器人的奇异空间对工业机器人完成指定任务(如码垛、喷漆、焊接、抛光等工作)具有前瞻性指导意义。根据D-H参数法建立模型,利用数值算法求其在多姿态下的雅克比矩阵条件数,将此作为评判指标来衡量机器人在空间各个节点位置处的奇异程度,并用不同颜色将其可视化。可视化结果表明所划分的奇异区域满足理论中的两大奇异点范畴,从仿真结果看提出的算法切实有效。
机器人;工作空间;奇异点;可视化
机器人末端执行器上某个参考点的可达工作区域称为机器人机构的可达工作空间,简称为工作空间,可达空间指的是机器人只能以有限种姿态到达点的集合[1],机器人的奇异位形灵活空间是指在工作空间中机器人可以以任意姿态达到的点。机器人的工作空间奇异性是机器人的固有属性,在奇异点附近,机器人会丧失一个或几个自由度,使其利用数值法求出的逆解失效。研究机器人的奇异性离不开对机器人雅可比矩阵的研究,目前评判机器人灵巧性的指标有条件数[2]、最小奇异值、运动灵巧性[3]及可操作度[4]。国内外已有许多学者对机器人的奇异点进行了研究。林瑞麟[5]针对球形手腕机器人采用离散方法,通过对子系统奇异的研究,分析了整体系统的奇异问题;徐文福[6]针对PUMA类型机器人提出了一种“奇异分离+阻尼倒数”的方法,无需估计最小奇异值,但末端执行器精度较低;董伯麟[7]基于阻尼最小二乘法,给出一种连续阻尼自适应调节方法,增强了求解结果的稳定性,但这种方法需要同时比较4个算子的最小值,运算量较大,求解速度较慢;王红等[8]引入运动灵巧性指标对机器人的运动灵巧性进行了尺度综合分析,但其是否可以应用在串联机器人上目前尚不确定。
本文基于雅可比矩阵条件数,提出了一种在单位置节点多姿态下的加权条件数值,并充分考虑了在逆解不存在时雅可比矩阵的情况,提出一个新的标量来描述单位置下的奇异程度,使得在找出奇异位置的同时,能够将空间的奇异区域用颜色差异在空间中以可视化形式直观展示。
1 机器人模型建立
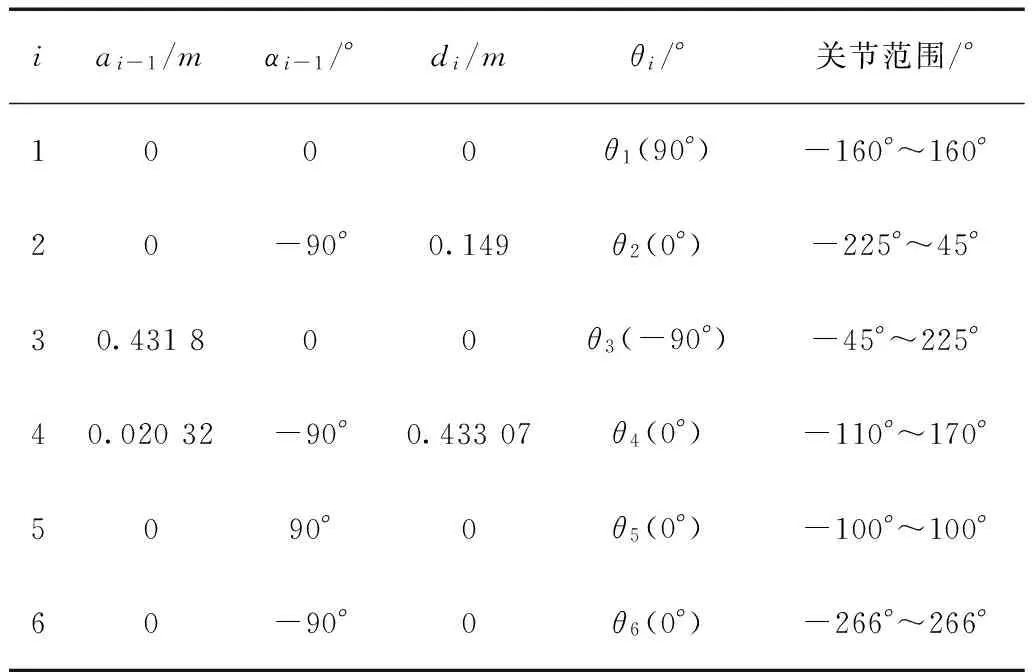
本文以Puma560机器人为例进行仿真,Puma 560结构参数见表1。
表1 Puma560的结构参数
iai-1/mαi-1/°di/mθi/°关节范围/°1000θ1(90°)-160°~160°20-90°0.149θ2(0°)-225°~45°30.431800θ3(-90°)-45°~225°40.02032-90°0.43307θ4(0°)-110°~170°5090°0θ5(0°)-100°~100°60-90°0θ6(0°)-266°~266°
Denavit和Hartenberg于1995年提出了一种为关节链中的每一杆件建立坐标系的矩阵方法,即D-H参数法,根据D-H参数法建立的Puma560机器人模型如图1所示。
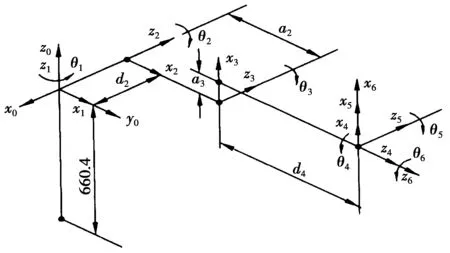
图1 Puma560机器人模型
2 机器人的工作空间
Puma560机器人的6个关节均为转动关节,前三个转动关节确定参考点位置,后三个关节组合成的腕关节决定其末端执行器的姿态[9-14]。通过几何法求得机器人最远可达边界D=a2+d4=0.864 87;内部边界d=d2=0.149 09;机器人的实际工作空间应是半径为D的外球体除去半径为d的内球体所剩余的球壳区域。半剖后的Puma560机器人工作空间示意图如图2所示。
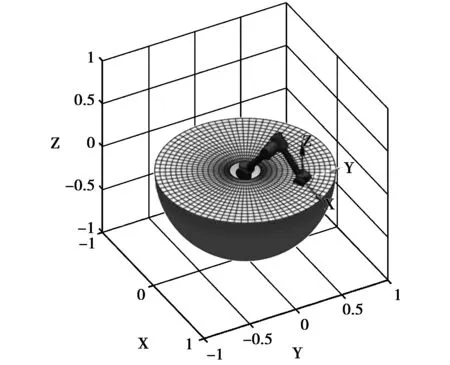
图2 Puma560机器人工作空间
机器人的雅可比矩阵为操作空间向关节空间的一种映射关系,对于本文研究的6自由度机器人而言,其雅可比矩阵可表示为:
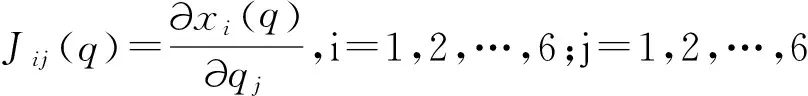
对于Puma560,其雅可比矩阵为6×6的矩阵,其中对于任一指定的列数j,前三行代表末端执行器对j关节线速度的传递比,而后三行则表示末端执行器对j关节角速度的传递比。
由于机器人的雅可比矩阵与位置坐标的3个变量及方位欧拉角的3个变量有关,本文提出一种“分而治之”的数值处理方法:先固定位置坐标(px,py,pz),让三个欧拉角等步长转过0°~360°得到不同转角下对应的姿态矩阵,然后再求出其雅可比矩阵信息。
3 6R机器人条件数的算法及其实现
对于串联机器人Puma560,由关节i至关节i-1的连杆变换为:
由此可求得其雅可比矩阵为:
其中,关节1~3的雅可比列各元素分别如下:
式中:si、ci、sij、cij分别表示sinθi、cosθi、sin(θi+θj)、cos(θi+θj),i=1,2…6。
本文对机器人末端执行器的三个方位角等步长各取10个值,组合共计103种不同的姿态,在这些姿态中,也有逆解不存在的位姿点。在算法中,当判断出某些位姿点用数值法求不出逆解时,会对这部分位姿点进行赋值操作,使这些位姿点也具有雅可比条件数值。最后将每个位置节点多种姿态下的条件数值进行数值运算,求得其加权条件数值。算法流程图如图3所示。
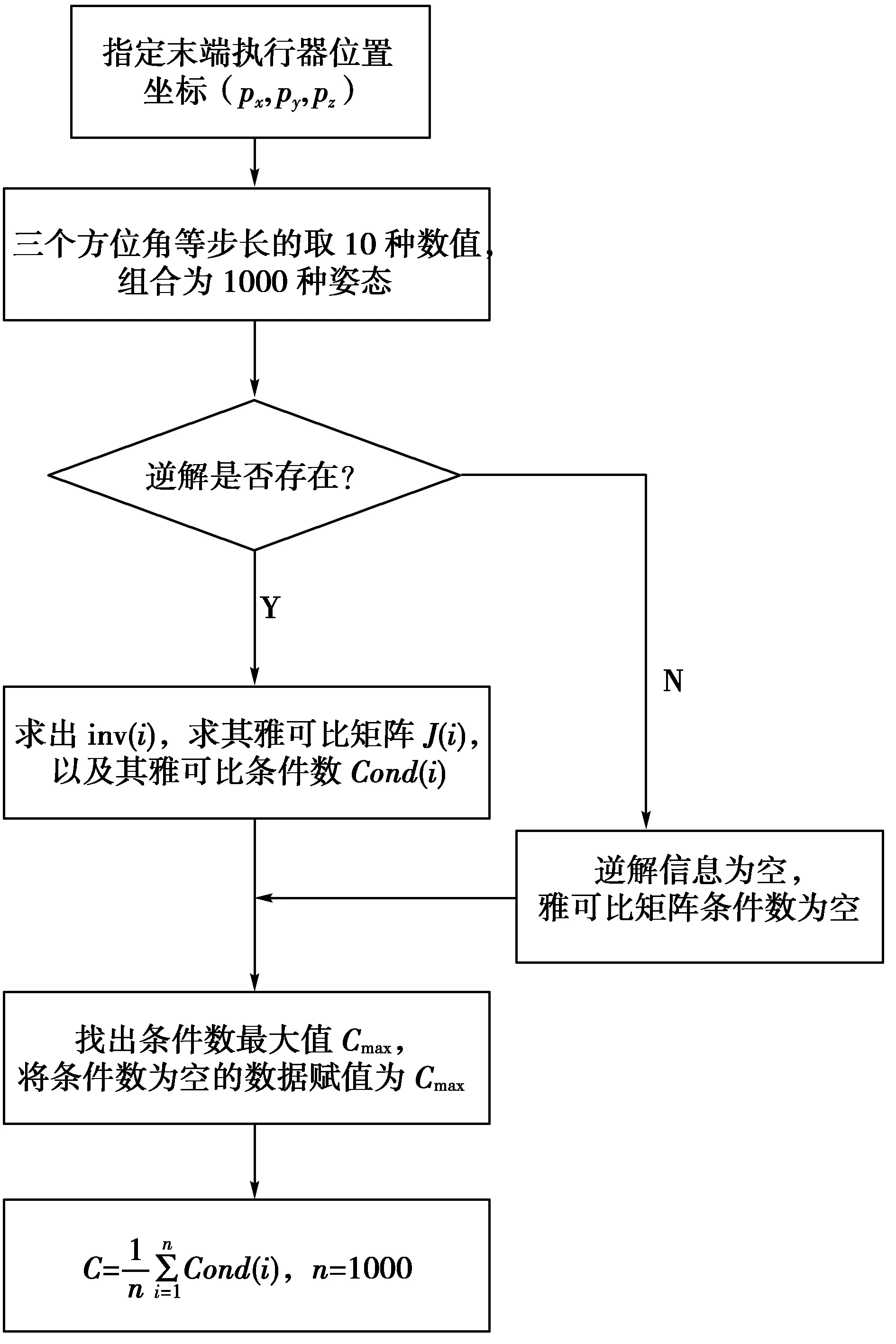
图3 算法流程图
4 6R机器人工作空间奇异程度的可视化展示
本文选取了Z=0.2的平面,对此平面按极坐标的形式进行网格划分,扇形半径从0.15~0.85等分为15份,扇形角度从0~π等分为41份,所取的样本工作点共有615个。
本文提出用一个新的标量α来描述奇异程度,若将条件数的最大值记作Cmax,cond记作条件数,则奇异度α可表示为:
在Z=0.2平面下选取的部分数据见表2。
表2 Z=0.2平面部分节点坐标及其对应的α值
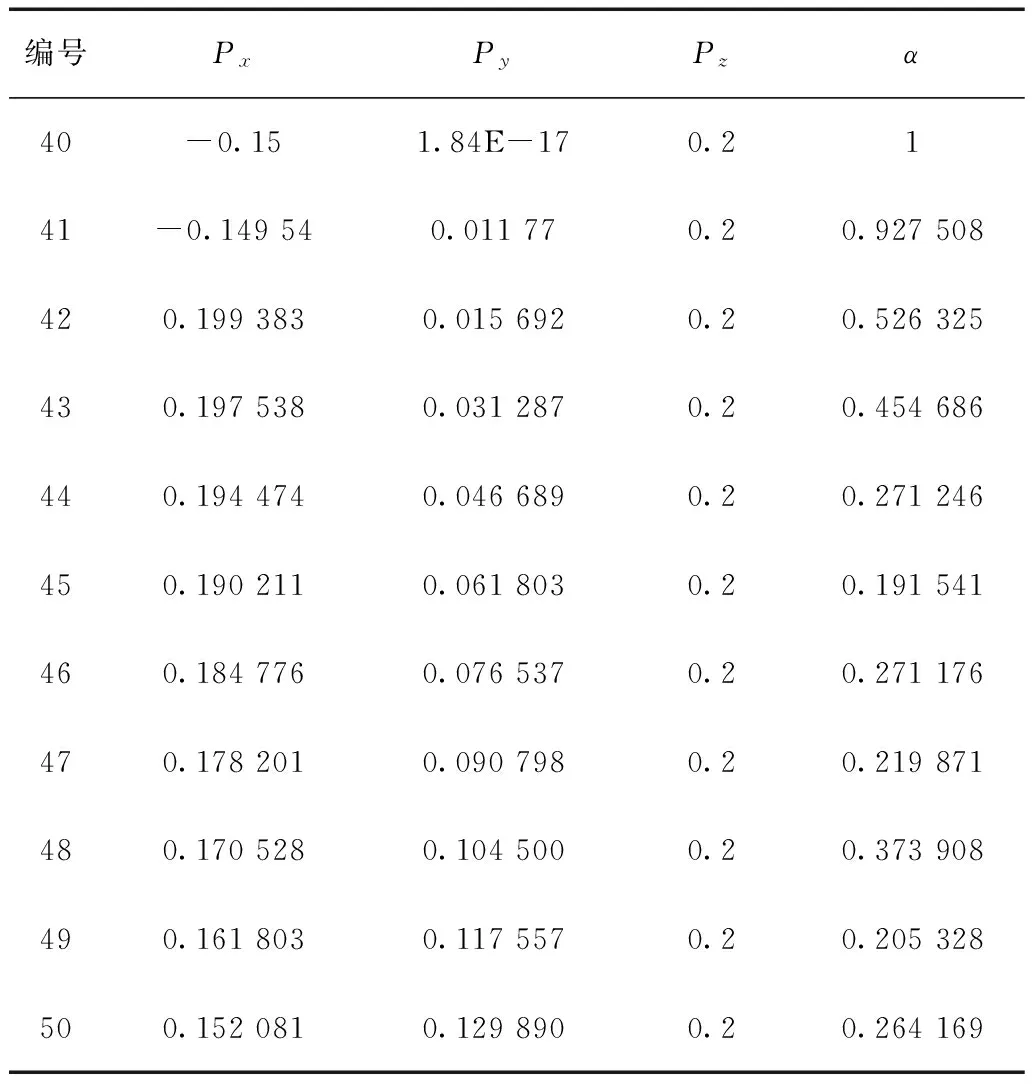
编号PxPyPzα40-0.151.84E-170.2141-0.149540.011770.20.927508420.1993830.0156920.20.526325430.1975380.0312870.20.454686440.1944740.0466890.20.271246450.1902110.0618030.20.191541460.1847760.0765370.20.271176470.1782010.0907980.20.219871480.1705280.1045000.20.373908490.1618030.1175570.20.205328500.1520810.1298900.20.264169
由α的定义式可知,0<α≤1。α值越大,代表奇异程度越大,利用网格节点的α值来表征网格的颜色,以此得出的Z=0.2平面下的机器人工作空间奇异程度如图4所示。

图4 Z=0.2平面下的机器人工作空间奇异程度
由奇异性和灵巧度与雅可比矩阵条件数的关系可知,条件数越大,即α越大,表现为机器人的灵巧性越差,其奇异程度也越大。由图4中可以直观地看出,在内边界与外边界的值偏大,事实上这正是机器人奇异形位中的“边界奇异”。除此之外,在中间部分也有部分奇异度很高的点,这些对应于机器人奇异形位中的“内部奇异形位”,这是由于某些关节轴线重合,使机器人丧失了自由度所致。
5 结果与仿真
在工作空间中随机选取两点A、B(见图4),为了避免末端执行器在笛卡尔空间中的轨迹如黑色直线穿过空间中的奇异点,在A、B之间再插入14个中间点。仿真时间为2 s,等分为16份,第i个时间点对应于执行器到达轨迹中的第i个节点的位置,关节1~6的关节角度随时间的变化曲线如图5所示。
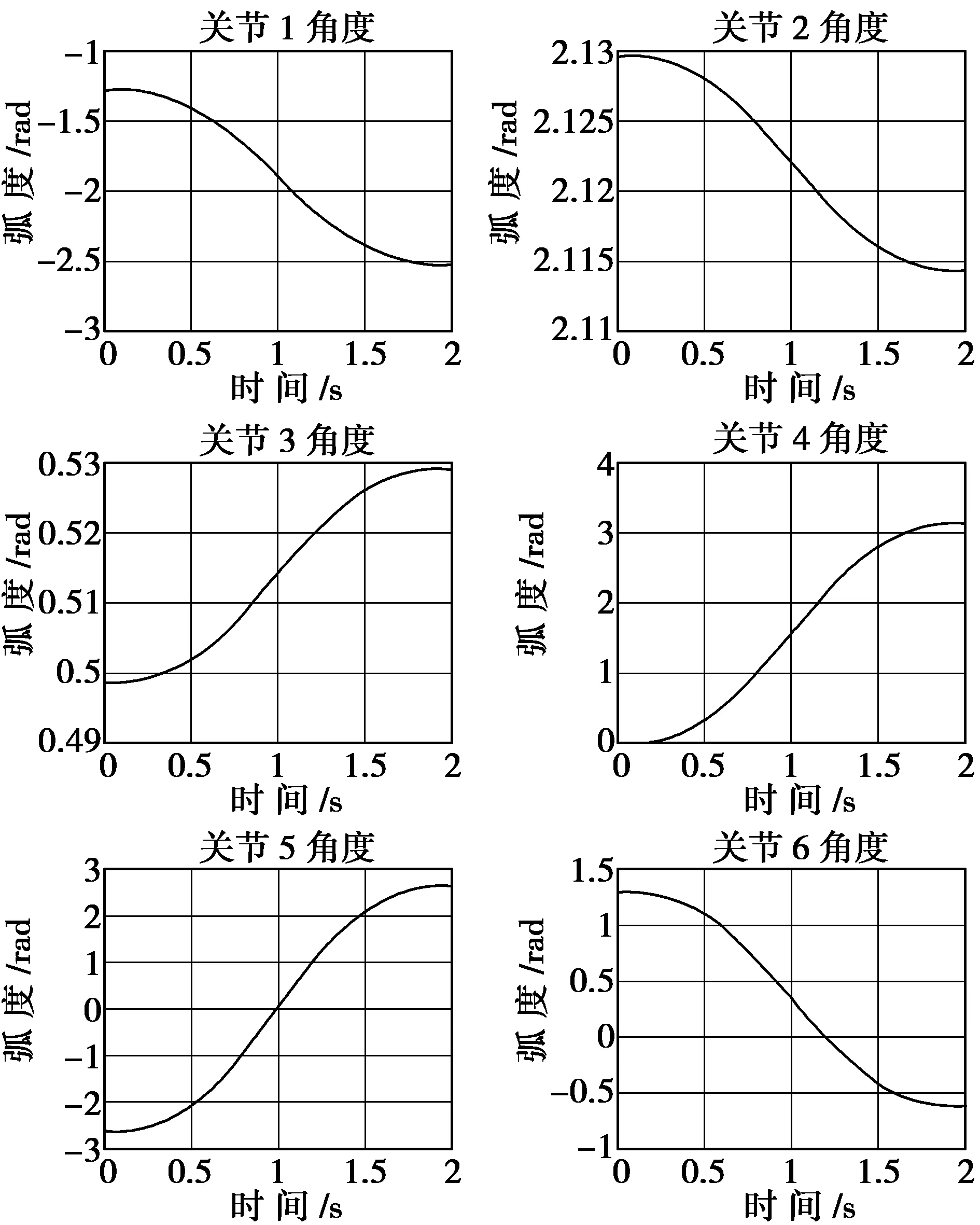
图5 关节角度随时间的变化曲线
本文对关节空间轨迹规划采用三角函数插值法,由图5可以看出,关节1~6的角度均没有超出表1中的转角范围,速度随时间变化平缓,没有速度突变节点。
6 结论
(1)给出了一种描述串联机器人奇异程度的数值计算方法,提出了一个新的标量来评价工作空间中各个节点甚至各个区域的奇异程度,仿真结果表明切实可行。
(2)对于如喷漆、弧焊之类的工业机器人在一个指定平面内的工作,本文提供的方法可有效地预测奇异位形,并可通过图形可视化的方式展示出来。
(3)实际工程中,在机器人指定初末位置任务的情况下,为机器人末端执行器考虑避开奇异点的路径规划问题提供了理论依据。
[1] 熊有伦.机器人技术基础[M].武汉:华中科技出版社,1996.
[2] Salibury JK,Craig J.Articulated Hands:Kinematic and Force Control Lessure[J].Int.J.of Robotics Research,1982,1(1):4-17.
[3] Angeles J,Rojas A A.Manipulator Inverse Kinematics Via Condition Nurmer Minimization and Condituation[J].Int.J.of Robotics and Automation,1987,2(20):61-69.
[4] Yoshikawa J.Manipulability of Robotics Mechanisms[J].Int.J.Robotics Research,1987,4(2):3-9.
[5] 林瑞麟.机械手奇异分析和判断[J].华侨大学学报,1998,19(2):174-179.
[6] 徐文福.一种新的PUMA类型机器人奇异回避算法[J]自动化学报,2008,34(6):670-675.
[7] 董伯麟,彭航,工业机器人逆运动学的奇异回避算法[J].机械设计与研究,2016,32(2):35-40.
[8] 王红,孙晓红.基于灵巧特性的三平动并联机构的尺度综合研究[J].机床与液压,2016,44(15):5-7.
[9] 苏学满,孙丽丽,杨明,等.基于Matlab 的六自由度机器人运动特性分析[J].机械设计与制造,2013(1):78-80.
[10] 韩晓建,杨卫杰,高寰宇,等.基于连杆机构的四足仿生机器人运动学分析及足迹优化[J].森林工程,2017,33(1):52-58.
[11] 谢斌,蔡自兴.基于MATLAB Robotics Toolbox 的机器人学仿真实验教学[J].计算机教育,2010(19):140-143.
[12] 杨卫杰,孟兆新,秦国新.联合采伐机六足行走装置单足力学解算与分析[J].森林工程,2015,31(1):66-69.
[13] 张刚,黄海波.HP20 机器人的运动学逆解计算及模拟仿真[J].轻工机械,2011,29(6):40-45.
[14] 洪庆,曲跃军,刘影,等.山地步行式拖拉机及造林机具的研究[J].林业机械与木工设备,2015(7):24-25.
(责任编辑 张雅芳)
Visual Study on the Singularity of the Workspace for 6R Serial Manipulators
FU Xiao, TAN Yue-sheng
(School of Technology,Beijing Forestry University,Beijing 100083,China)
The analysis of the singular space of the robots is of prospective guiding importance for industrial robots to complete such specified tasks as stacking,painting,welding and polishing.A model is constructed with the D-H parameter method,and a numerical algorithm is used to obtain condition number of Jacobian under multi-pose,which is used as an evaluation indicator to measure the degree of the singularity of each node in the space,with different colors used to visualize the workspace.The results of visualization shows that the region of the proposed singularity match with the two kinds of singular points in previous theory,and the proposed algorithm is effective seen from the simulation results.
robot;workspace;singular point;visualization
2017-01-20
符 晓(1991-),男,河南南阳人,硕士研究生,主要从事机器人运动动力学的研究,E-mail:fx034592@126.com。
TP242
A
2095-2953(2017)04-0032-04

