改进型神经网络在木件打磨机器人中的应用

张连滨， 葛浙东， 鞠明远， 刘存根， 周玉成

(山东建筑大学信息与电气工程学院，山东 济南 250101)

研究与设计

改进型神经网络在木件打磨机器人中的应用

张连滨， 葛浙东， 鞠明远， 刘存根， 周玉成

(山东建筑大学信息与电气工程学院，山东 济南 250101)

针对木件机械打磨加工效率低、产品质量差等问题，提出一种打磨轨迹跟踪算法，该算法是对模糊算法和神经网络算法的结合及改进。阐述了打磨机器人的系统结构，并针对两关节机器人建立动力学模型，基于打磨轨迹跟踪算法设计了模糊神经网络控制器。利用Simulink软件对打磨轨迹跟踪算法进行仿真试验，结果表明：改进型神经网络与传统神经网络算法相比，0时刻开始，跟踪误差均在±0.01 mm范围内，系统很好地完成了启动控制，并且打磨机器人在1 s时即可以实现极小误差的曲线打磨轨迹跟踪。该算法可有效控制打磨机器人的运动轨迹，工作时机器人运行稳定可靠，加工效率高。

木件打磨机器人；轨迹跟踪；模糊算法；Simulink仿真

机器人代替人力劳动是衡量一个国家工业化水平的重要标志之一，机器人自动化、智能化程度越来越高是科技进步的表现，其中打磨机器人就是利用机器人的人工智能完成木件打磨工作[1]，以确保木件上胶后的表面光滑。目前国内的工厂大多是由工人手持抛光机对木件进行半自动化抛光，这种方式作业速度慢、效率低，而且工人操作存在技术上的差异，容易出现尺寸误差，影响整体效果。另外，加工过程中产生的大量木屑会对操作人员的身体造成伤害，因此实现机器人高精度打磨抛光作业已引起人们的高度重视[2-6]。

国内外对打磨机器人的研究很多，J H Alm[7]开发了一种基于五轴打磨机器人和气动打磨头的智能打磨系统来改善模具表面的质量；Luis等[8]提出了一种基于高水平任务图像描述的机器人抛光任务自动规划方法；黄玉钏[9]通过建立六自由度打磨机器人运动学模型获得了机器人运动学的正反解，在运动学的基础上设计了机器人张量积曲面的路径规划方案。机器人打磨木件时，因木件并非结构化，密度和硬度均存在差异，而且在打磨作业过程中还存在各种动力学非线性和不确定性的干扰，故需要采用智能控制策略来提高打磨机器人的轨迹跟踪性能。

本研究设计了一种将模糊算法和神经网络算法相结合的打磨机器人控制方案。这种改进型神经网络与传统神经网络相比，可以补偿机械臂打磨环境的不确定性，使网络的学习与系统的实际轨迹跟踪过程相适应，为打磨机器人完成木件的高精度打磨提供了更可靠的方法，具有较好的实时性和很大的优越性。

1 打磨机器人系统与工作流程

打磨机器人系统组成如图1所示，其主要由机器人主车、机器人副车、机器人控制柜、人机交互界面、打磨工具、废屑处理装置、力-力矩传感器及位置控制器等组成。其中，机器人主车包括机械手臂的支撑装置和进给装置，用来保证打磨工具的进给和整个机械臂的支撑；机器人副车用来运输和固定打磨工件；力-力矩传感器安装在机器人末端，用来测量所受力和力矩的大小；打磨工具安装在力矩传感器的测量面，用来实时反馈力矩信息；人机交互界面用来规划打磨工具在待加工木件上的打磨路径，其输出和机器人控制柜相连。

打磨机器人的木件打磨过程为：首先机器人副车将待打磨木件运送到指定位置固定，人机交互界面对待打磨工件的路径进行规划，并将规划完的机器人末端位置信息传递给位置控制器，位置控制器驱动机器人到达指定位置开始打磨。同时，力-力矩传感器测量打磨工具和打磨木件之间力的大小，并将测量的信息传递给力控制器，力控制器根据测量的信息对机器人进行调节以保持打磨工具和加工件之间的力相对恒定。最后，废屑处理装置将打磨完的废屑进行处理，以保证整个打磨效果。

2 打磨机器人动力学建模

打磨机器人的机械手可以看作是一个开链式刚性多连杆机构。机器人末端操作器与木件等打磨面接触时，其动力学方程[10-11]如下：

(1)

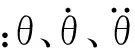
3 神经网络控制器设计

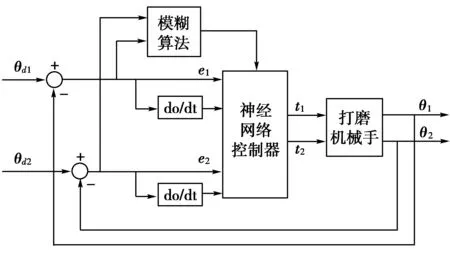
图2 神经网络控制器设计θd1、θd2.两关节的期望位置；θ1、θ2.两关节的实际位置；e1、e2.两关节的位置误差；ec1、ec2.两关节的位置误差变化率；t1、t2.作用于两关节的转矩

打磨机器人通过神经网络控制器实时跟踪打磨轨迹，在训练初期，采用模糊算法优化系统启动跟踪控制，随着打磨过程的进行，控制器综合考虑系统的参考输入θd1、θd2和跟踪误差e1、e2，使模糊算法的输出及其变化ec1、ec2趋于零，逐步取消模糊算法的作用，使机器人打磨路径逼近理想打磨轨迹。

3.1 神经网络模型建立

神经网络是一种采用高斯型基函数来实现输出层同隐含层之间映射的神经网络。根据打磨机器人系统的特点，以机器人打磨位置偏差和偏差变化率为控制器输入层函数，以作用于机器人的转矩作为输出层目标，构建神经网络模型。

(1)输入层：其节点的输出为：

f1(i)=xi

(2)

(2)隶属函数层：该层的每个节点具有隶属函数的功能，对第j个节点：

(3)

式中：cij和bj分别为第i个输入变量的第j个集合高斯函数的均值和标准差。

(3)规则层：该层通过与模糊化层的连接来完成模糊规则的匹配，各个节点之间实现模糊运算，每个节点j的输出为该节点所有输入信号的乘积，即：

(4)

(4)输出层：该层每个节点的输出为该节点所有输入信号的加权和，即：

(5)

式中：l为输出层节点的个数；w为输出节点与第三层各节点的连接权矩阵。

3.2 模糊算法优化神经网络权值和阈值

利用模糊算法优化神经网络的初始权值和阈值，以便在解空间时能够确定较好的搜索空间，防止神经网络的搜索陷入局部极值。具体优化算法如下：

(1)模糊化：设打磨机械臂接近工作面的方向为正方向，远离工作面的方向为负方向。位置误差e1、e2，位置误差变化量ec1、ec2和控制量U的模糊集如下：

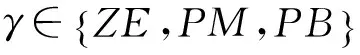
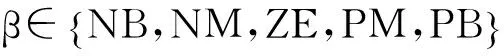
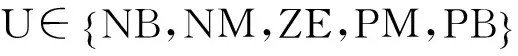
(2)建立模糊控制规则：结合打磨机器人在抛光木件等物件时的控制经验，对模糊控制的规则定义如下：①误差e1、e2较小，而且误差不变时，即误差变化率ec1、ec2为0，此时机械臂砂轮正沿着理想轨迹运行；②当误差变化率ec1、ec2变化较大时，说明机械臂末端正在偏离期望轨迹，这时则需要调整机械臂砂轮打磨的进给速率。模糊规则见表1。

表1 模糊规则表

Uec1、ec2ZEPMPBNBZENMNBNMZENMNBe1、e2ZEZEPMPBPMZEPMPBPBZENMNB

(3)反模糊化：对应输入模糊论域中的相应元素，查模糊控制查询表，求得模糊输出量，再乘以输出量化因子即可得到实际输出量。将模糊化输出量的各个元素与其相对应的论域相乘取平均值。在本文中采用面积重心法将模糊控制量转化为清晰的量，根据定义的规则，调节速度比率，从而维持一个相对稳定的加工过程。

3.3 模糊神经网络训练

取ym(k)=f4，ym(k)和y(k)分别表示网络输出和理想输出。网络输入为u(k)和y(k)，网络输出为ym(k)，则网络逼近误差e(k)为：

e(k)=y(k)-ym(k)

(6)

(1)采用梯度下降法来修正可调参数，定义目标函数为：

(7)

(2)修正输入隶属函数参数：

其中，

(8)

(3)隶属函数参数学习算法为：cij(k)=cij(k-1)+Δcij(k)+α(cij(k-1)-cij(k-2))bj(k)=bj(k-1)+Δbj(k)+α(bj(k-1)-bj(k-2))

(9)

(4)通过以下方式来调整输出层的权值：

(10)

则输出层的权值学习算法为：

w(k)=w(k-1)+Δw(k)+α(w(k-1)-w(k-2))

(11)

式中：η为学习速率；α为动量因子。

模糊神经网络控制器综合考虑了系统的参考输入和跟踪误差，通过上述的算法，不断逼近理想打磨轨迹，使模糊算法的输出及其变化趋于0，从而逐步取消模糊算法的作用，实现对系统的高精度跟踪控制。

4 Simulink仿真结果与分析

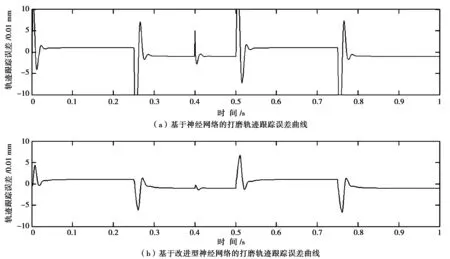
图3 基于神经网络与改进型神经网络打磨轨迹跟踪曲线对比

图3(a)为基于神经网络算法的打磨轨迹跟踪误差曲线，从中可以看出机器人打磨初期误差较大；图3(b)为采用改进型神经网络算法的打磨轨迹跟踪误差曲线，从0时刻开始，跟踪误差均在±0.1 mm范围内，系统能很好地完成启动控制，在1 s内即可很好地完成打磨轨迹跟踪，明显比采用传统神经网络算法打磨效果好。

5 结论

(1)神经网络学习算法在机器人打磨路径规划中具有较强的实用性，可以解决木件机械打磨、加工过程中产品加工质量差等问题。

(2)提出了模糊算法和神经网络学习算法相结合的控制方案，并构建了机器人打磨系统，其适用于打磨机器人路径规划，而且比传统神经网络学习算法更具优越性，对纤维板、刨花板、颗粒板的原材料加工和生产具有广泛的应用价值。

[1] 贺廉云.楼道清洁机器人的设计[J].农业装备与车辆工程，2012，50(8)：71-73.

[2] 张秀珩，柳洪义，罗忠.基于旋量理论的打磨机器人位置精度分析[J].机床与液压，2016，44(19)：29-33.

[3] 汪源，朱伟，沈惠平.一种复杂曲面打磨机器人自适应贴合柔性机构研究[J].机械科学与技术，2015，34(8)：1171-1176.

[4] 蔡小娜，张国梁，何燕丽，等.基于遗传算法和BP神经网络的竹粉模压花盆跌落冲击响应预测[J].木材加工机械，2016，27(2)：17-20.

[5] 杨卫杰，孟兆新，秦国新.联合采伐机六足行走装置单足力学解算与分析[J].森林工程，2015，31(1)：66-69.

[6] 崔曦元，杨茉.自主行走管道清洗机器人设计[J].林业机械与木工设备，2016，44(8)：19-21.

[7] J H Ahm.Intelligently Automated Polishing for High Quality Surface Formation of Seulptured Die [J].Journal of Materials Processing Technology，2002(130 /131)：339-344.

[8] Luis Basanez，Jan Rosell.Robotic Polishing Systems[J].IEEE Robotics & Automation Magazine，2005(9)：35-43.

[9] 黄玉钏.六自由度打磨机器人张量积曲面轨迹规划仿真[J].计算机仿真，2015，32(7)：348-351.

[10] 张立勋，卜迟武.风机叶片打磨机器人的动力学控制[J].机械设计，2011，28(6)：29-32.

[11] Tian F，Li Z，Lv C，et al.Polishing pressure investigations of robot automatic polishing on curved surfaces[J].International Journal of Advanced Manufacturing Technology，2016，87(1-4)：1-8.

(责任编辑 张雅芳)

Application of Improved Neural Network in Woodpiece Polishing Robot

ZHANG Lian-bin， GE Zhe-dong， JU Ming-yuan， LIU Cun-gen， ZHOU Yu-cheng

(School of Information and Electrical Engineering，Shandong Jianzhu University，Jinan Shandong 250101，China)

In view of the problems of low polishing efficiency and poor product quality of wood machinery，the paper puts forward a polishing trajectory tracking algorithm，which is a combination and also improvement of a fuzzy algorithm and a neural network algorithm.Firstly，the robot manipulator’s polishing system composition is stated，a kinetic model is established based on two-joint robots and based on the polishing trajectory tracking algorithm，a fuzzy neural network controller is designed.Simulink software is used to conduct simulation testing on the polishing trajectory tracking algorithm，with the result showing that compared with the traditional neural network algorithm，the improved neural network starts at 0：00，with tracking error within 0.01mm，the system able to complete startup control wonderfully.The polishing robot can realize curve polishing trajectory tracking in 1s.This algorithm can be used to effectively control the trajectory of polishing robots，contributing to the stable and reliable robot operation during work and high processing efficiency.

woodpiece polishing robot；trajectory tracking；fuzzy algorithm；Simulink simulation

2017-01-13

山东省泰山学者优势特色学科人才团队支持计划项目(2015162)；博士基金项目“基于X射线的木结构建筑用材无损检测系统研究”(XNBS1622)

张连滨(1991-)，男，山东肥城人，在读硕士研究生，主要研究方向为智能控制与机器人系统，E-mail：869017798@qq.com。

TS642

A

2095-2953(2017)04-0019-04