基于可信性理论的投资组合优化问题研究

韩文倩��

摘要建立了基于可信性理论的投资组合模型，包括风险最小的单目标均值方差模型和收益最大的单目标均值方差模型，运用拉格朗日乘数法对两个模型进行了求解，给出了2个模型解析解的表达式，并通过数值算例验证了模型的可行性.对两个模型的结果进行对比，发现风险最小化和收益最大化的单目标均值—方差模型得到的结果基本吻合.

关键词投资组合；可信性测度；梯形模糊数

中图分类号F830.59 文献标识码A

1引言

投资组合选择就是如何配置有价证券的头寸来符合投资者风险最小受益最大的要求[1].在证券市场这个极其复杂的系统中，证券的收益和风险都具有不确定性，这就使得投资者在一个不确定的环境下做出投资决策.1952年，Markowitz在假设投资者都是厌恶风险的前提下建立了在预期收益的基础上使得风险最小的投资组合模型[2].由于证券市场中预期收益率和风险大小的存在不确定性，而建立在概率论基础上的模型并未考虑这种不确定性[3].因此大量学者对该模型进行了研究和改进，将风险和收益的不确定性加入到模型中[3-7].2004年，清华大学刘宝碇教授等给出了基于测度论的模糊数学公理化体系可信性理论[8].本文参考Markowitz的均值方差模型，运用可信性理论来计算模糊变量的数学期望和方差，建立了在预期收益率一定的前提下使得风险最小的模糊投资组合优化模型和风险一定的前提下使得预期收益率最大的模糊投资组合优化模型，并且运用拉格朗日乘数法对模型进行求解，得到投资组合最优解的一般表达式，另外，通过实证分析对本文提出的模型进行了验证.

2风险最小的模糊投资组合优化模型

2.1模型的建立与求解

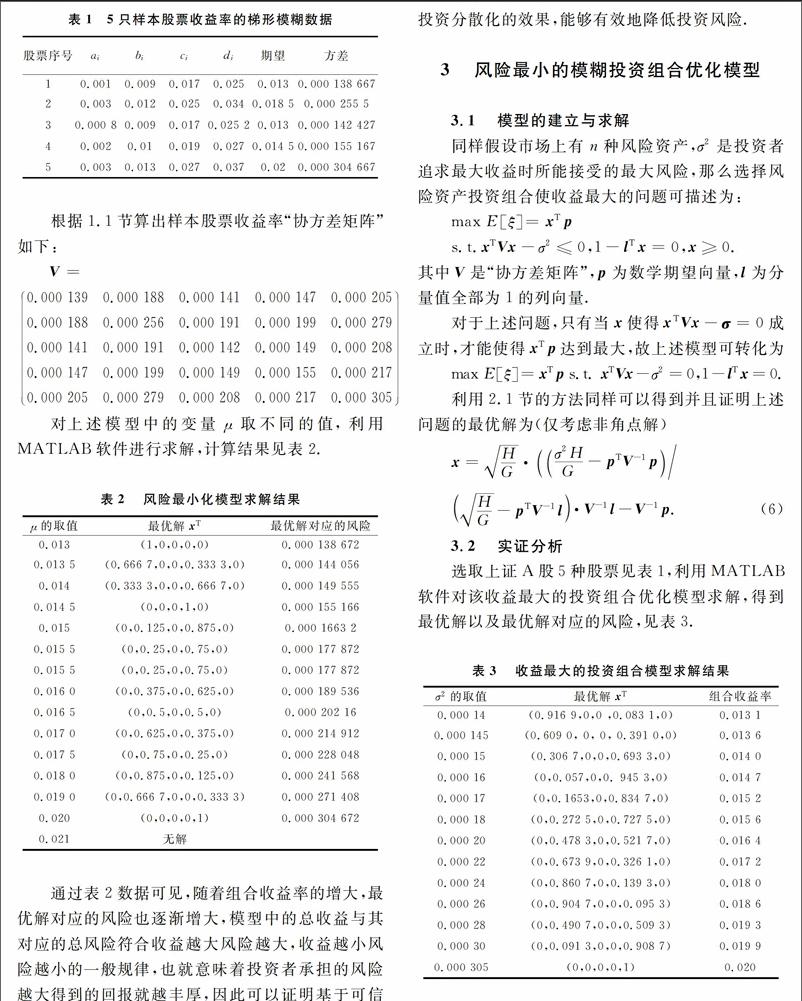
通过表3数据可以观察到，随着最优解对应的风险随着组合收益的增大而增大，模型中的總收益与总风险符合收益越大风险越大的规律，投资者想要得到更大的收益就意味着要承担更大的风险，因此可以证明基于可信性理论所建立的收益最大的投资组合模型的可行性和有效性，模型所得到的投资策略能够达到投资分散化的效果，能够有效地降低投资风险，增大收益.

最后对表2和表3中的数据进行比较，通过对比可见，对于给定的样本数据，2个模型几乎是重合的，在个别区间存在微小差异，但是从总体来看，2种模型的投资结果不存在较大差异性，也就是说在投资者只追求单一目标时，由于另一个参考因素的限制，导致最后的最优组合不会有太大的差异.

4结论

一般情况下，投资者的预期收益越大，他所承担的风险就越大，不同的投资者对获利性的要求都有不同，但无论其预期收益如何，总希望能找到一组投资组合，使其实现预期收益率的概率最大.本文结合了可信性理论来改进原有投资组合选择的均值方差模型，并在改进模型的基础上对若干股票进行了数值计算，验证了模型的可行性，以期为我国证券市场投资组合问题的研究提供一种可行有效的方法.

参考文献

[1]张银利，高淑萍，邱言玲.投资组合选择的一种模糊决策方法[J] .数学实践与认识，2013，43（20）：50-56.

[2]房勇，汪寿阳.模糊投资组合优化-理论与方法[M].北京：高等教育出版社，2005.

[3]邓雪.带有梯形模糊数的均值—方差投资组合模型比较分析[J].经济数学，2011，28（3）：49-54.

[4]陈国华，陈收，房勇，汪寿阳.带有模糊收益率的投资组合选择模型[J].系统工程理论与实践，2009，29（7）：8-15.

[5]臧东冉，林亮，刘星子.含随机变量的资产投资组合优化模型[J].统计与决策，2009，25（1）：146-148.

[6]唐惠，钟庆平.基于随机占优约束的投资组合优化模型研究[J].财经界，2015，31（1）：108-110.

[7]刘燕武，张忠桢.基于实际收益率分布的均值-方差-条件风险价值多目标投资优化模型[J].系统管理学报，2010， 19（4）：444-450.

[8]刘宝碇，彭锦.不确定理论教程[M].北京：清华大学出版社，2005： 74-118.