像素交叉移位变换耦合动态和谐搜索优化机制的图像加密算法
丁汀, 王晓侃
(1. 河南机电职业学院 信息工程学院, 河南 新郑 451191;2. 河南机电职业学院 机电工程学院, 河南 新郑 451191;3. 北京交通大学 电子信息工程学院, 北京 100044)

像素交叉移位变换耦合动态和谐搜索优化机制的图像加密算法
丁汀1, 王晓侃2,3
(1. 河南机电职业学院 信息工程学院, 河南 新郑 451191;2. 河南机电职业学院 机电工程学院, 河南 新郑 451191;3. 北京交通大学 电子信息工程学院, 北京 100044)
提出一种像素交叉移位变换耦合动态和谐搜索优化机制的图像加密算法.首先,引入锯齿填充曲线,对明文进行扫描,形成一维像素序列;基于明文像素位置,定义像素交叉移位变换模型,耦合均布Logistic映射输出的密钥,对明文完成高效置乱.然后,定义新的和谐更新模型,以密文信息熵值与相关性为目标函数,改进动态和谐搜索机制,构建像素扩散函数,彻底改变置乱图像的像素值.最后,引入HASH检测函数,赋予算法认证功能.结果表明:与当前混沌加密技术相比,所提算法具有更高的加密安全性和通用性. 关键词: 图像加密; 像素交叉移位变换; 锯齿填充曲线; 动态和谐搜索; 像素搜索变换; HASH检测函数
图像包含了诸多信息与秘密,是当前用户常用的介质,给各行业带来了巨大便利[1-2].然而,由于数字图像在免费的网络环境中传输,容易遭受到未知授权的攻击,使图像信息被窃取,带给用户巨大的隐患[3].因此,对图像进行加密保护,防止信息被窃取显得非常重要[4].但经典数据加密算法并没有综合考虑图像的大数据容量与较高的冗余度等特性,难以用于数字图像加密[5].为此,诸多学者设计了相应的数字图像的加密技术.当前主流的加密算法是基于混沌系统的加密机制[6-8],这种加密技术虽然取得了较好的保密效果,但该技术过度依赖混沌参数,缺乏大尺度传播效应,无法加密非方形明文,且随着混沌系统的周期性迭代,其混沌行为会逐步衰落,从而降低了算法的安全性.本文提出一种像素交叉移位变换耦合动态和谐搜索联合优化机制的图像加密算法,并进行仿真实验.
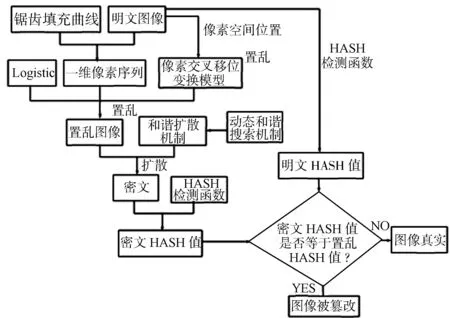
图1 文中算法的加密过程Fig.1 Encryption process of this algorithm
1 图像加密算法设计
为了避免混沌加密技术的不足,设计了像素交叉移位变换耦合动态和谐搜索优化机制的图像加密算法来提高安全性,其加密过程如图1所示.
1.1 基于像素交叉移位变换模型的明文置乱
令初始图像的大小为M×N,通过引入锯齿填充曲线[9],对明文进行扫描,形成一维像素序列P={P(0),P(1),…,P(M×N-1)}.由于传统的raster,Zigzag及Hilbert填充曲线[10]的置乱度不高,且只能用于方形图像的扫描,故文中基于锯齿曲线模型,定义了锯齿扫描机制.锯齿曲线示意图,如图2所示.其计算模型为
(1)
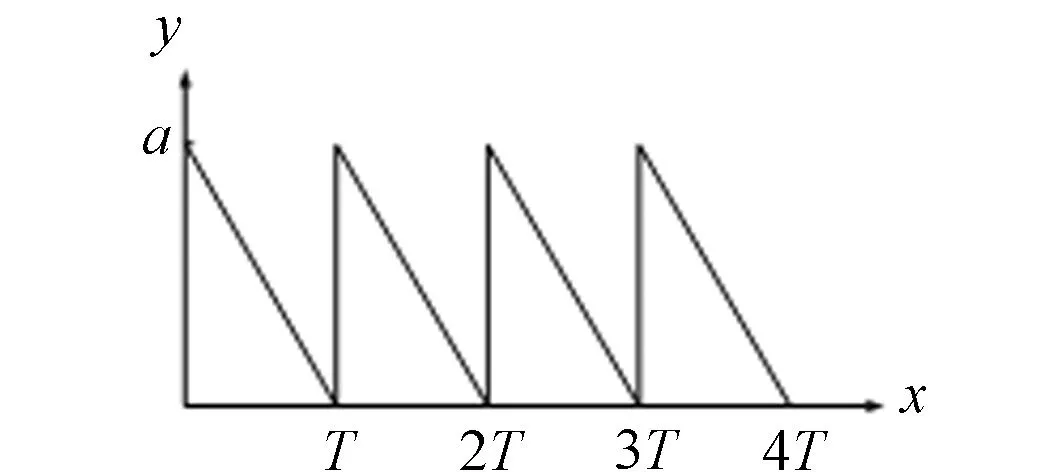
图2 锯齿曲线示意图Fig.2 Sketch map of saw tooth curve
式(1)中:a为曲线的高度;T为曲线周期.
由图2可知:该锯齿扫描模型是由连续的若干个直角三角形组成,利用锯齿扫描模型,通过对三角形中的3个点完成一次整体遍历,将明文像素形成一维数组,实现初始置乱.
由P={P(0),P(1),…,P(M×N-1)},计算像素交叉位置,可得
(2)
式(2)中:P(L-1)为前一个混淆像素的灰度值;L为当前像素位置;L′为像素交叉后的新位置;Sp(L)为均布Logistic映射的输出密钥,其模型为
(3)
式(3)中:Xi+1,Xi分别为式(3)的第(i+1),i个迭代值;λ为控制参数,当-4≤λ≤4时,映射是混沌的.
因此,根据式(2)计算得到的像素位置L′,设计像素交叉移位变换机制,即
(4)
(5)
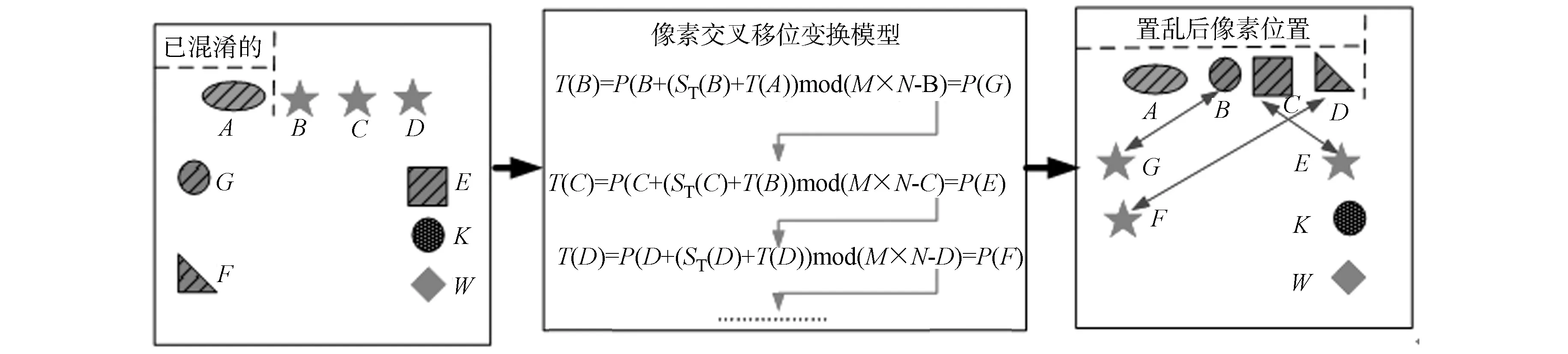
图3 像素交叉移位变换机制Fig.3 Pixel cross shift mechanism

图4 像素G的交叉移位变换Fig.4 Cross shift of pixel G
为了直观描述像素交叉移位变换模型,在初始图中任意选择7个像素,如图3,4所示.如果图像中的像素A之前的像素均被扰乱,则剩下的像素B,C,D均是交叉移位变换目标,如图3所示.借助像素B,C,D,实现与像素E,F,G位置的变换.如果两个初始图像的像素G有微弱的差异,令其灰度值分别为P(G),P(G′).由式(4)可知:位置的差异会影响到像素C的变换.依据图4,像素P(C)被移位变换为P(K),图像中剩余像素以此类推.利用像素交叉移位变换机制处理明文,能够高度置乱其像素位置.
为了衡量所提像素交叉变换模型的置乱率,将文献[11]视为对照组,通过计算两种算法的置乱率进行评估.置乱率模型[12]为
(6)
式(6)中:Lsd,LSD为混淆前后图像的小波系数方差值;u为归一化因子.
1.2 基于动态和谐搜索机制的像素扩散
为了改变像素值,构建置乱-扩散的加密体系,提高算法的安全性,引入和谐搜索(HS)算法[13],定义像素扩散模型,改变图像像素灰度值.HS算法主要是模拟音乐演奏,即一个音乐家搜寻一个更优美和谐状态过程的方法[14].
1.2.1 目标函数的确定 和谐搜索实质是一个优化更新过程,通过最小的成本获取最大的利益,故其目标函数为

(7)
式(7)中:F(X″)为全局函数;X″为设计参数;LB(j),UB(j)分别为第j个参数的下边界、上边界.
然而,文中加密技术目的是最大化密文的信息熵Hm[8]与最小化相邻像素的相关性Cx,y[9],故定义新的目标函数为
(8)
(9)
(10)
式(8)~(10)中:L为图像灰度级别;p(mi)为像素mi出现的几率;x,y分别为图像中任意相邻的两个像素点的灰度值;n为相邻点的数量;E()为均值.
1.2.2 和谐记忆库的初始化 在进行目标搜索更新之前,需要对其参数完成初始化.令X″i=(Xi(1),Xi(2),…,Xi(n)),它是和谐记忆库中的第i行谐音,则和记忆库中的每一个谐音都可被初始化为
(11)
式(11)中:r为[0,1]内的随机数.
依据模型(11)完成初始化后,形成了和谐记忆矩阵HM,即
(12)
为了提高和谐搜索机制的初始参数的随机特性,利用HM中的奇数和偶数的搜索引擎视为明文图像的宽度和高度,故模型(11)中的系数UB(j),LB(j)分别为
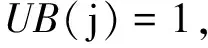
(13)

(14)
式(14)中:W,H分别为明文图像的宽度与高度.
依据模型(13),(14)可获取密钥 Xi,即
(15)
(16)
式(15),(16)中:i为HM当前所在位置的引擎.
对于任意的明文,其宽度W与高度H都是常量.因此,对于任意的奇数或偶数j,模型(16)是一个线性函数.文中可以确保密钥流的偶数或奇数引擎元素分别分布在[1,W],[1,H]中.
1.2.3 谐音的更新 在图像加密技术中,每个加密过程中的谐音都是一个密钥.因此,定义了新的谐音更新模型,在加密期间,文中算法能够不断更新谐音,产生新的密钥,使该技术具有较高的随机动态性与安全性.
在所提加密技术中,新的谐音生成方法有:1) 和谐记忆依恋率(HMCR);2) 音调调整率(PAR);3) 随机重新初始化.
对此,为了生成新谐音Xnew(j),首先,在[0,1]内生成一个随机数r1,若r1低于HMCR,则Xnew(j)必须依据式(17),从和谐记忆库HM中选择;否则,根据式(11)随机生成,即
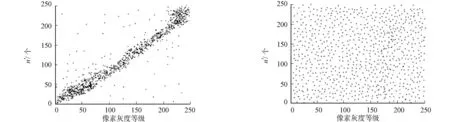
(17)
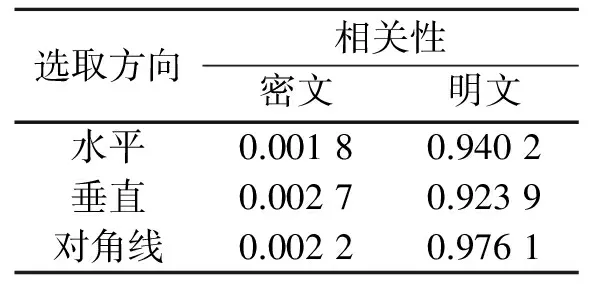
若Xnew(j)是从HM中选择,将得到另外一个随机数r2∈[0,1].最终,r2将与音调调整率PAR完成比较,若r2 (18) 式(18)中:BW(j)为第j个谐音的带宽. (19) (20) 式(19),(20)中:W,H分别为明文图像的宽度与高度. 通过迭代和谐动态搜素算法,使模型(8)的输出值最大.此时的Xnew(i)即最佳密钥,利用此密钥,完成像素扩散. 1.2.4 基于搜索变换模型的像素扩散 由于像素交叉移位变换只能改变其空间位置,无法变换其灰度值,故基于动态和谐搜索机制,利用该机制输出的密钥Xnew(j),定义搜索变换模型,以完成像素扩散,最大化密文的信息熵值为 (21) 1.3 基于HASH函数的图像信息认证 引入HASH检测函数[15],估算扩散密文与初始明文的HASH值,对图像是否被篡改进行认证.若初始明文大小为I,经过和谐搜索扩散后,最终密文为I″,则图像信息真伪决策过程有以下3个步骤. (22) 步骤3 令初始明文I,扩散密文I″的HASH值分别是H1(i),H2(i),如果H1(i)=H2(i),则表明文中算法安全可靠,明文在传输过程中有效抵御了攻击;如果H1(i)≠H2(i),则表明所提加密技术安全性不高,明文在传输期间遭受到篡改. 采用Matlab工具对文中算法的加密安全度进行验证.同时,为体现文中算法的优异性,将当前安全性较高的文献[6]、文献[16]加密算法视为对照组.初始密钥为:r=0.5,LB=1,a=8,T=4,λ=3,x0=0.35,r2=0.75,HMCR=0.6. 2.1 加密质量对比分析 文中算法的通用性测试,如图5所示.首先,以非方形明文(图5(a))为目标,利用文中算法对其完成加密,验证所提技术的通用性与安全性.由图5可知:文中算法能够对非方形目标完成置乱与扩散,且具有较高的加密质量(图5(b),图5(c)).这是因为文中算法定义了像素交叉移位变换模型,使其不受明文尺寸限制. (a) 非方形明文 (b) 文中算法的置乱结果 (c) 文中算法的加密结果 图5 文中算法的通用性测试Fig.5 Universal testing of algorithm in paper 3种算法的加密效果,如图6所示.由于文献[6]、文献[16]无法加密非方形目标,为了体现公平性,将方形明文(图6(a))视为测试对象,利用文中算法与文献[6]、文献[16] 对其完成加密.由图6可知:从视觉上看,3种加密技术都具有较好的可靠性,明文的信息都被有效隐藏. (a) 初始明文 (b) 文中算法 (c) 文献[6] (d) 文献[16]图6 3种算法的加密效果Fig.6 Encryption effect of three algorithms 为了量化3种算法的安全性差异,利用密文信息熵H(m)进行评估[17].测试数据显示:文中算法拥有最高的H(m)值,达7.995 2,非常接近8;而文献[6]、文献[16]的H(m)值分别为7.971 6,7.987 9.这是因为文中加密技术定义了定义像素交叉移位变换模型,高度置乱明文,并利用动态和谐搜索算法扩散置乱图像,最大化密文的熵值.文献[6]则是通过融合2个低维Arnold映射和Logistic映射,增加置乱与扩散的关联性,从而对图像完成加密,但低维映射的加密安全性不高.文献[16]虽然考虑了时间延迟现象,提高了序列的伪随机特性,但其主要依靠四维超混沌系统实现像素扩散,在迭代期间,因混沌周期性而降低算法的安全度,导致其密文的H(m)值略低于文中算法. 2.2 抗差分攻击能力测试 像素变化率(NPCR)与统一平均变化强度(UACI)是评估加密技术抗击差分攻击能力的常用指标,故通过测试密文的NPCR与UACI曲线进行量化.3种算法的NPCR与UACI曲线,如图7所示.图7中:n为迭代轮数. 由图7可知:文中算法通过联合锯齿填充曲线与像素交叉移位变换模型,彻底扰乱像素位置,并利用动态和谐搜索机制改变图像像素值,通过不断地迭代优化,使其NPCR与UACI值最大化;文献[6]、文献[16]主要依赖混沌轨迹实现像素的扩散,而混沌系统在反复迭代过程中,因其周期性而降低其混沌行为与窗口,导致算法的安全性均低于文中算法. 由图7还可知:文中算法与文献[6]具有相当的加密效率,只需两轮置乱-扩散迭代,算法就趋于收敛,NPCR与UACI值达到了稳定值,而文献[16]虽然保密程度高于文献[6],但文献[16]是迭代四维超混沌Chens系统改变像素值,增大了算法的复杂度,需要经过4轮迭代才能进入收敛状态. (a) NPCR值测试结果 (b) UACI值测试结果图7 3种算法的抗差分攻击能力测试Fig.7 Resist differential attack test resluts of three algorithms 2.3 相邻两个像素点的相关性分析 明文相邻像素之间的强烈相关性最容易给攻击者留下攻击线索,故加密技术通常需要降低此种相关性[16].任意择取1 000对相邻像素点,依据文献[16]计算二者的相关Cx,y.文中算法消除Cx,y的测试结果,如图8所示.图8中:n′为像素分布数量. (a) 明文图像 (b) 密文 图8 文中算法的相关性测试Fig.8 Correlation test of this algorithm 由图8可知: 明文的相关性非常剧烈,聚集为对角线, 而利用所提加密技术对其置乱-扩散后,有效降低了Cx,y,其值约为0.001 8.空间上另外2个方向的Cx,y测试结果,如表1所示.由表1可知:文中算法具有较高的可靠性,能大幅度削弱图像相邻像素的相关性,提高图像传输安全度. 表1 3个方向的相关性测试 为了提高加密算法的适应性与安全性,设计了一种新的加密技术,通过定义像素交叉移位变换,使算法不受明文尺寸的限制,可对非方形明文完成置乱.通过替换传统和谐搜索机制的目标函数,形成了一种动态和谐搜索算法,完成像素加密.今后的研究将考虑引入水印技术进一步提高算法的安全性. [1] 刘冰,潘大兵.新三维混沌映射及其在数字图像信息加密中的应用[J].华侨大学学报(自然科学版),2015,36(6):655-658. [2] HUANG Xiaoling.Image encryption algorithm using chaotic Chebyshev generator[J].Nonlinear Dynamics,2012,67(4):2411-2417. [3] ZHU Congxu,LIAO Chunlong,DENG Xiaoheng.Breaking and improving an image encryption scheme based on total shuffling scheme[J].Nonlinear Dynamics,2013,71(1/2):25-34. [4] ZHANG Xuanping,ZHAO Zhongmeng.Chaos-based image encryption with total shuffling and bidirectional diffusion[J].Nonlinear Dynamics,2014,75(1):319-330. [5] 朱晓升,廖晓峰.基于图像分区的置乱算法[J].计算机技术与发展,2015,25(12):52-55. [6] 谢国波,丁煜明.基于Logistic映射的可变置乱参数的图像加密算法[J].微电子学与计算机,2015,12(4):111-115. [7] 柴秀丽,甘志华.基于超混沌系统的位级自适应彩色图像加密新算法[J].计算机科学,2015,38(6):149-152. [8] YE Guodong.A block image encryption algorithm based on wave transmission and chaotic systems[J].Nonlinear Dynamics,2014,75(3):417-427. [9] SMREK A,EXANDER Y G.A novel family of space-filling curves in their relation to chromosome conformation in eukaryotes[J].Physica A: Statistical Mechanics and Its Applications,2013,392(24):6375-6388. [10] 胡亦,王琳娜,朱恭生.锯齿空间填充曲线耦合压缩感知的彩图灰度化实时加密算法[J].激光杂志,2015,26(12):12-18. [11] 曹光辉,贾丹,张毅智.基于超混沌序列的图像加密方案[J].计算机应用研究,2013,30(10):3110-3113. [12] 范铁生,张绍成,张忠清.小波域局部标准差的图像置乱评价方法[J].微电子学与计算机,2014,35(4):931-935. [13] HUANG Ming,GUO Shujie,XU Liang.Application of improved harmony search algorithm in test case selection[J].Journal of Software,2014,9(5):1170-1176. [14] MOHAMMED S A.A hybrid harmony search algorithm for ab initio protein tertiary structure prediction[J].Network Modeling Analysis in Health Informatics and Bioinformatics,2012,1(3):69-85. [15] SONG Guangjia,JI Zhenzhou.Novel duplicate address detection with Hash function[J].Plos One,2016,11(3):e0151612-e0151619. [16] YE Guodong,WONG K W.An image encryption scheme based on time-delay and hyper-chaotic system[J].Nonlinear Dynamics,2013,71(1):259-267. [17] 徐亚,张绍武.基于Arnold映射的分块双层自适应扩散图像加密算法[J].中国图象图形学报,2015,20(6):740-748. (责任编辑: 钱筠 英文审校: 吴逢铁) Image Encryption Algorithm Based on Pixel Cross Shift Transform Coupling Dynamic Harmony Search Optimization Mechanism DING Ting1, WANG Xiaokan2,3 (1. College of Information Engineering, Henan Mechanical and Electrical Vocational College, Xinzheng 451191, China;2. College of Mechanical and Electrical Engineering,Henan Mechanical and Electrical Vocational College, Xinzheng 451191, China;3. College of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044, China) The image encryption algorithm based on pixel cross shift transform coupling dynamic harmony search optimization mechanism was proposed in this paper. Firstly, one dimensional pixel sequence was obtained by introducing the saw tooth filling curve to scan the plain; and the plain was permutated by defining the pixel cross shift conversion model based on plain pixel location and coupling the key outputted by Logistic map for enhancing its general performance. Then the dynamic search diffusion model was constructed by the dynamic harmony search mechanism to completely change the pixel value of the permutation image; and finally, the HASH function was introduced to gives the authentication function to this algorithm. Test results show that: this algorithm has higher encryption security and generality compared to the present chaotic encryption technique. Keywords: image encryption; pixel cross shift transform; saw tooth filling curve; dynamic harmony search; pixel search trsnsform; HASH detection function 10.11830/ISSN.1000-5013.201702018 2016-01-26 丁汀(1972-),女,副教授,主要从事图像处理和数据挖掘的研究.E-mail:happy3305@sohu.com. 河南省重点科技攻关项目(132102210385); 河南省教育技术装备和实践教育研究基金资助项目(GZS013) TP 391 A 1000-5013(2017)02-0229-07
2 实验结果与分析


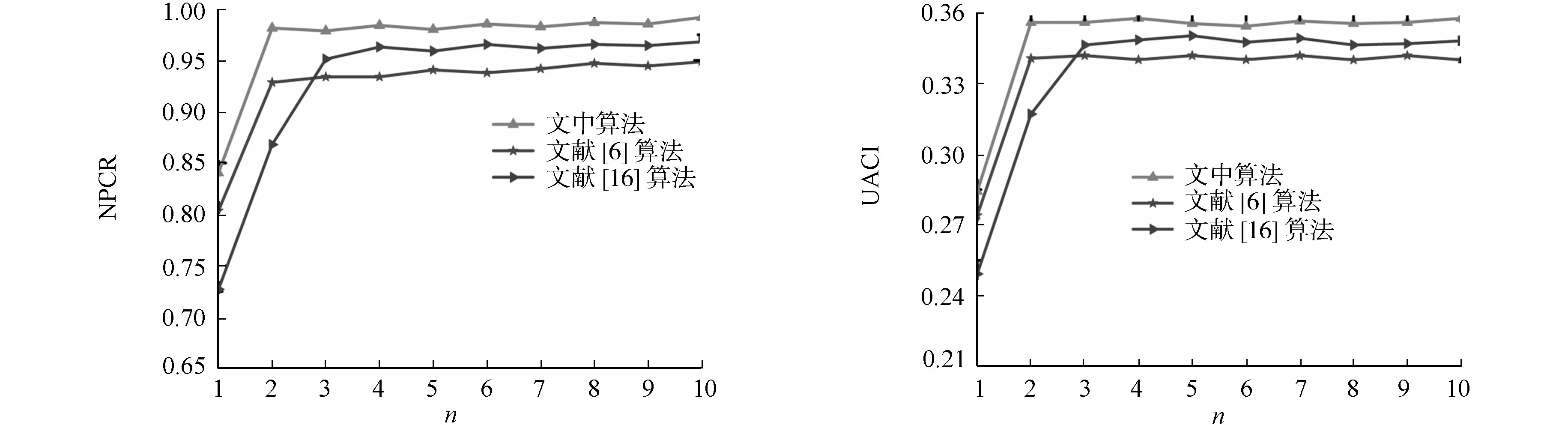
3 结束语

