基于有向线段重构轮廓与成对几何直方图的缓解阀盖图像匹配算法

赵大兴 王 博 周唯倜 孙国栋

湖北工业大学机械工程学院， 武汉， 430068

基于有向线段重构轮廓与成对几何直方图的缓解阀盖图像匹配算法

赵大兴 王 博 周唯倜 孙国栋

湖北工业大学机械工程学院， 武汉， 430068

针对货运列车缓解阀盖缺失故障的检测，提出一种基于轮廓有向线段重构与成对几何直方图的匹配方法。该方法首先根据最大弦长和极半径确定采样初始位置，并根据局部弯曲度评价机制对轮廓进行动态分级采样；然后以采样点为端点按逆时针顺序构建有向线段，依次计算每对线段间的有向相对角和归一化当量距离，并最终将其作为该对线段的双重特征描述子计入二维直方图；最后使用巴氏距离对二维直方图间的相似性进行度量。实验分析表明，该算法对旋转、缩放和平移等几何变换有较好的鲁棒性，同时也兼顾了检测效率，满足了列车故障检测的实时性要求。

缓解阀盖；匹配；有向线段；成对几何直方图

0 引言

当前，我国铁路正向着“客运高速化”和“货运重载化”的方向快速发展，列车在高速重载条件下，其运行安全问题显得尤为重要。利用货运列车运行故障动态检测系统(trouble of moving freight car detection system，TFDS)快速准确地识别故障，可有效克服人工检测的随机性和局限性，对列车检测工作具有重要意义。轮廓是识别物体形状的最直观特征，基于轮廓的目标识别技术近年来已广泛应用于航空航天、军事、医学、传媒、农业、人工智能等领域，但在列车检测方面鲜有应用。吴晓雨等[1]提出一种改进的形状上下文算法，该算法利用寻找包含轮廓采样点数量最多的角度区间的方式改变图像角度，并计算对应区域的匹配代价，从而克服形状上下文无旋转不变性这一缺点；师文等[2]提出一种基于轮廓重构和特征点弦长的图像检索方法，该方法首先对轮廓进行降维重构，并在新定义的支持域内计算轮廓点的特征强度从而筛选出有效特征点，最后构建相应特征点和轮廓点间的弦长特征函数作为特征描述子，该方法在噪声样本库中具有良好的检索性能。

缓解阀[3]是货运列车制动系统中的重要组成部分，位于车体底部，当列车制动无法取消(闸瓦抱死轮对无法复位)时，通过拉动缓解阀将副风缸空气排出，从而使制动风管空气迅速向副风缸补充，使闸瓦离开轮对。由于列车运行中振动或其他人为因素，缓解阀盖缺失并使阀体暴露在外的现象时有发生，所造成的内部阀面缺油、扬尘堵塞、橡胶密封件加速老化等故障严重影响列车安全，同时因其位于列车底部，背景环境较为复杂，人工检测和TFDS识别均存在一定难度。本文结合现有研究成果，提出的缓解阀盖匹配识别算法几乎不受旋转、缩放、平移的影响，具有较强的鲁棒性。

1 缓解阀盖匹配识别流程

图1所示的白色矩形框标记部位即为缓解阀盖， TFDS系统[4]识别缓解阀盖的总体匹配识别流程如下：对采集的图像进行预处理和轮廓提取，选取图像区域内最大面积轮廓；结合轮廓极半径和最大弦长确定采样点初始位置，并通过三角形局部弯曲度评价单元及动态步长对轮廓进行动态采样；按逆时针方向依次连接各采样点，将轮廓重构为一系列首尾相接的有向线段集；分别以每一条有向线段为基础边，依次计算该有向线段与其他有向线段的归一化当量距离特征描述子和有向相对角特征描述子；最后，计算上述描述子的二维直方图作为轮廓整体特征，并通过Bhattacharyya距离[5]计算其与模板图像二维直方图[6]的相似度，从而完成对缓解阀盖的匹配识别。

图1 TFDS采集的缓解阀盖图像Fig.1 The image of release valve bonnet taken by TFDS

2 轮廓有向线段重构

2.1 图像预处理和目标轮廓提取

TFDS系统运行的复杂环境使得所采集图像不可避免地存在噪声干扰等情况，这将对后续轮廓有向线段重构和匹配特征提取产生严重影响。为确保得到缓解阀盖完整清晰的轮廓，采用颜色空间系数为12、坐标空间系数为3的6×6双边滤波[7]框对图像进行“保边去噪”处理，然后基于8连通Freeman链码提取目标图像轮廓，其中具有最大闭合面积的封闭轮廓即为缓解阀盖轮廓，如图2所示。

图2 缓解阀盖轮廓Fig.2 The contour of release valve bonnet

2.2 采样点初始位置的确定

轮廓采样点作为构建有向线段集的重要基础，决定了后续成对有向线段特征描述子的计算准确度和匹配精确度，因此采样前需以一个约定标准来确定采样初始位置及顺序，且使其不受尺度、旋转和平移等几何变化的制约。本文以轮廓极半径和最大弦长相结合的方式确定采样初始位置。

首先，定义轮廓C由点集{Pn|Pn=(xn,yn),n=1,2,…，T}构成，其中T为轮廓像素点总数。寻找轮廓内部的最大弦长，得其两端端点为Pi=(xi,yi)和Pj=(xj,yj)，端点对应像素点在原轮廓序列中的索引值为Ii=i、Ij=j；然后，设轮廓形心坐标为O(x0,y0)，其计算公式为

(1)

采用欧氏距离计算端点Pi和Pj处对应的极半径ρi与ρj，即

(2)

n=1,2，…，T

接着，比较上述两处极半径大小，极半径较大处对应的弦长端点即为轮廓采样初始点，将其在轮廓序列中的索引值置为0，即

(3)

最后，从索引值为0的点开始依次对序列中点的索引值进行重置，赋予轮廓新的点集顺序。

2.3 轮廓关键点采样

本文算法的核心思想是将大量成对有向线段的特征描述信息统计入一个二维直方图中，以该二维直方图作为轮廓的宏观特征描述，与模板进行相似性度量。为保证二维直方图描述的客观准确性，有向线段的总体数量的丰富度和轮廓关键位置有向线段的集中度需得到保证,即在局部轮廓较复杂的地方需增大采样点密集度，而在局部轮廓相对平缓处，采样点密集度无需增加。因此，本文提出一种基于局部弯曲度的分级动态步长规划采样算法。

2.3.1 基准步长的确定

通常情况下步长的确定以轮廓周长作为参考，若基准步长过大，则能忽略轮廓局部信息丰富之处，若基准步长过小，则会增加无谓计算量。大量实验表明，当轮廓重构有向线段数量不低于100时，最终二维直方图的描述准确性较好，因此基准步长初步定为轮廓周长的百分之一。然而，相同周长轮廓存在复杂度不同的情况，仅以周长作为参考所得基准步长并不完全适用。为此，本文引入了基准步长修正系数K：

K=4πS/L2

(4)

式中，S为轮廓面积；L为轮廓周长。

K值范围为(0,1]，其几何意义为：轮廓面积与同等周长圆面积的比值，当该比值趋近于1时，表示该轮廓近似于标准圆，当比值愈趋近0时，表示该轮廓很复杂。将K值作为对轮廓整体复杂程度的衡量指标，对基准步长进行修正，修正后的基准步长sB为

sB=TK/100

(5)

2.3.2 基于三角形单元的局部弯曲度评价机制

首先，取局部轮廓曲线段C′为研究对象，设C′上某点为起始点Pi，采样步长为s，则以s为间隔分别取第2点Pi+s和第3点Pi+2s，并以该3点构建三角形局部弯曲度评价单元，如图3所示。

图3 三角形局部弯曲度评价单元Fig.3 The triangular evaluation element oflocal curvature

然后，以该局部轮廓第1点和第3点所连接的弦长与其余两段弦长之和的比值，作为其局部复杂度，即

(6)

2.3.3 分级动态采样

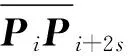
(7)

令二级动态步长s=s-sd，依次重新构建三角形局部弯曲度评价单元，直至Ei小于t或s≤4时将Pi和Pi+2s存入序列V。最后重置s=sB，再以Pi+2s作为下一步采样的起点。最终采样完成时，动态序列V的容量扩充为N，即有N个采样点。

2.4 有向线段构建

按原轮廓逆时针方向将序列V中N个采样点依次连接，则两两相邻的采样点即为各有向线段的首尾端点，共计N条有向线段，并将每段首尾分别标记为1和2，如图4所示。

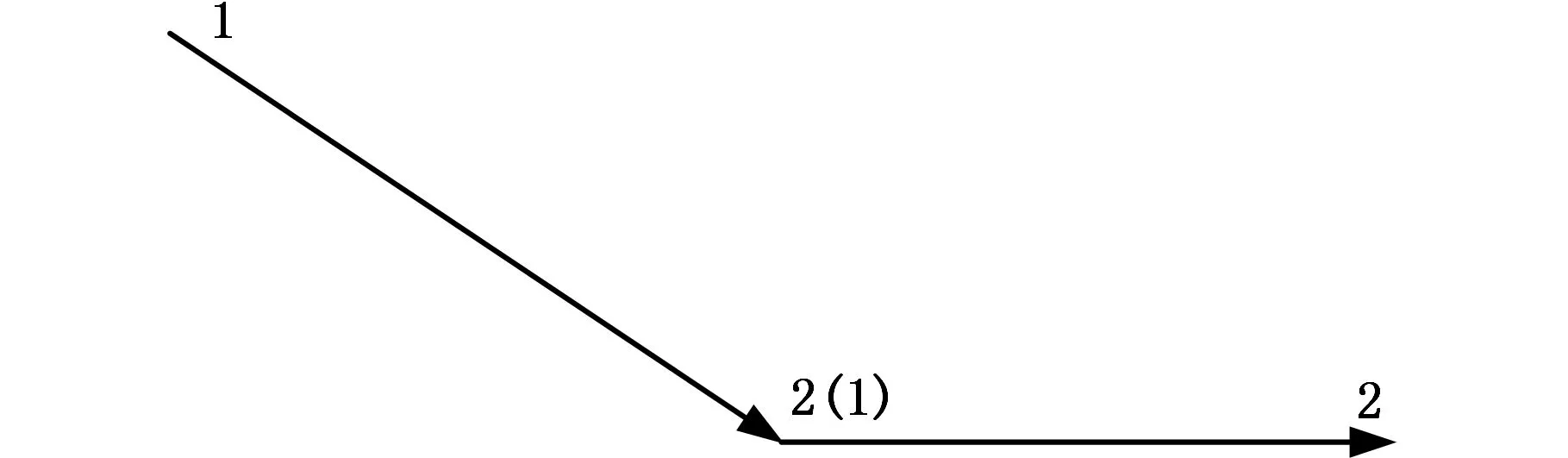
图4 有向线段示意图Fig.4 The sketch of oriented line segment

图5 轮廓有向线段重构Fig.5 Contour reconstructed by oriented line segment

3 改进的成对几何直方图匹配方法

链码编码直方图(chain code histogram，CCH)[7]是一种用来统计轮廓Freeman链码编码8种走向(用数字0～7表示)出现次数的直方图，而成对几何直方图[8](pairwise geometrical histogram，PGH)可认为是CCH算法思想的延伸应用，其核心思想是对目标轮廓特征信息进行统计，并将其纳入二维直方图，作为对目标形状的整体描述，其基本原理如图6所示。分别以不规则多边形的每一条边为基准边，依次计算其余边与基准边之间的最大距离dmax、最小距离dmin和夹角α，作为两条边的一组几何特征描述子，然后，用一个二维直方图统计上述所有特征描述子，如图7所示。

图6 PGH基本原理Fig.6 The rationale of PGH

图7 二维直方图中的一对有向线段特征描述子Fig.7 A pair of oriented line segment feature descriptors in two dimensional histogram

然而，在以缓解阀盖为目标对象的实验过程中发现，最终直方图匹配效果并不理想，出现了目标辨识度较差甚至误匹配的现象，同时尺度不变性也无法保证。为此，本文对原始成对几何直方图算法做进一步改进。

3.1 有向相对角

由图6可知，夹角α范围为(0,π/2]，针对100条以上线段两两之间构成的夹角而言，该范围显得过于集中，并不足以反映整体轮廓特征。为扩大特征描述子数据在直方图角度坐标的分布，增强特征描述子直方图的辨识度，本文以有向相对角βi取代原PGH算法中的夹角α，对直方图的角度范围进行拉伸处理。处理方法如下：基于2.3节中赋予重构线段的方向属性，任取一对有向线段为研究对象，以图8为例，在目标图像平面坐标系内，分别计算基准边m和其对应边n与X轴正向的方向角αXm、αXn，则有向相对角βi为

(8)

由式(8)可知，有向相对角βi的大小与所选坐标系无关，对旋转具有不变性，同时由于赋予了有向线段方向属性，使得βi的范围扩展为(0,2π)。

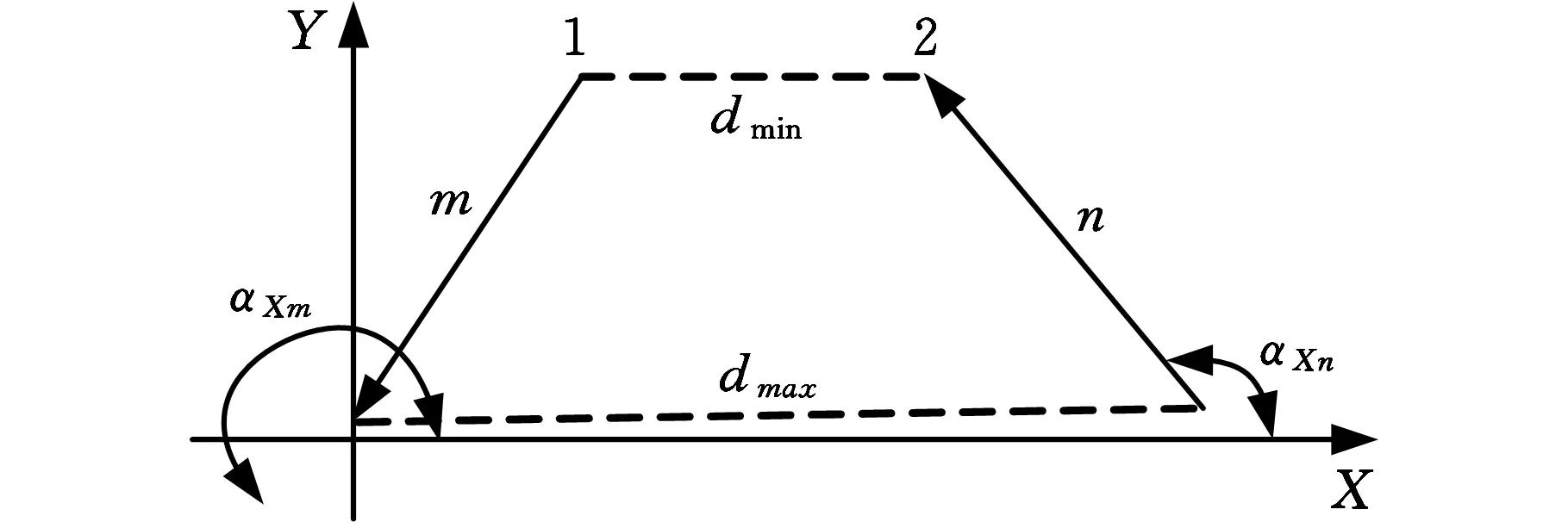
图8 成对有向线段示意图Fig.8 The sketch of pairwise oriented line segment

3.2 归一化当量距离

由图7二维直方图可知，在有向相对角范围十分接近的情况下，若成对有向线段的最大最小距离范围(dmin,dmax)存在重合，则在直方图中势必会产生相互干扰。本文约定一个当量距离Di，用单一变量Di来描述成对有向线段间的距离特征，从而避免最大最小距离范围(dmin,dmax)描述轮廓整体特征时直方图出现叠加干扰的现象。Di的计算公式为

(9)

考虑到TFDS系统是在列车运行期间动态采集图像[9]，拍摄环境比较复杂，为保证轮廓描述的尺度不变性，对当量距离Di进行归一化处理。设最大当量距离为Dmax，归一化当量距离R表示为

(10)

至此，将每对有向线段的两种描述子相互关联，便构成了其特定的成对有向线段特征描述子组合(βi,Ri)。为验证有向相对角描述子和归一化当量距离描述子针对目标图像几何变换的鲁棒性，对缓解阀盖图像进行缩放和旋转以及轮廓有向线段重构，如图9所示。将其成对描述子去关联化后分别统计入对应一维直方图，为便于比较，将各频率直方块顶端连接，折线化处理，同时隐去直方块，如图10所示，各条折线十分接近，说明上述两种描述子对缩放、旋转等变化均具有良好的不变性，鲁棒性较强。

(a)原始轮廓(b)旋转30°，缩放0.8倍

(c)旋转-96°，缩放1.1倍图9 经缩放和旋转变化的轮廓有向线段重构Fig.9 Contour reconstructed by oriented line segment after scale and rotation transformation

(a)有向相对角在几何变化下的频率分布

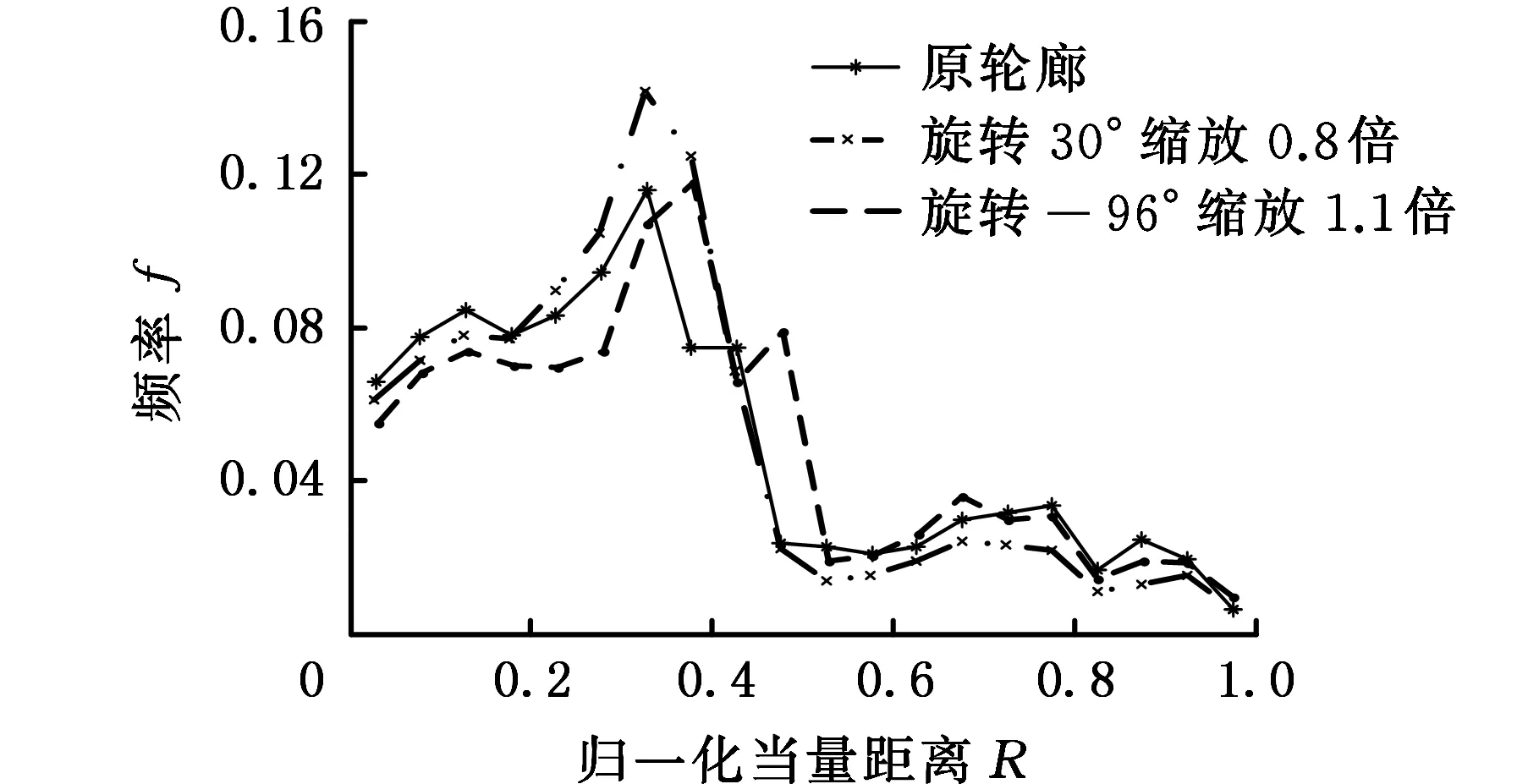
(b)归一化当量距离在几何变化下的频率分布图10 成对特征描述子在几何变化下的频率分布Fig.10 The frequency distribution of geometric transformed pairwise feature descriptors

3.3 成对几何直方图

将所有成对有向线段特征描述子组合(βi,Ri)统计入一个二维直方图，其中两个维度分别为有向相对角β和归一化当量距离R，并分别选取适当的均分组数(数据范围除以组距所得值)，该二维直方图即为成对几何直方图。为在平面视图中直观展现二维直方图视觉效果，本文对经直方图统计的数据结果进行标准化处理，将其范围限定在[0,255]之间。原立体直方块在垂直视角下变为二维平面上的投影方格，将原直方图标准化处理的数据作为灰度值赋予对应二维平面方格内的所有像素点，此时方格的亮暗程度即可直观反映出原直方块的高低程度，如图11所示，其中有向相对角均分组数为18，归一化当量距离均分组数为10。

图11 改进的成对几何直方图Fig.11 Improved pairwise geometrical histogram

3.4 直方图相似性度量方法

作为对目标整体轮廓特征的统计描述，成对几何直方图之间的相似性度量也是缓解阀盖匹配识别十分重要的一个环节，其度量方法的优劣直接影响到匹配识别的最终效果。以匹配准确性为主要考虑因素，在常用的几种直方图相似性度量方法中选择Bhattacharyya距离来衡量本文成对几何直方图的相似性，其计算公式为

(11)

其中，H1(i)表示模板直方图中第i组频率；H2(i)表示目标直方图中第i组频率；DB∈[0,1]，DB值越小，表示相似度越高，反之相似性越低。

4 实验分析

如图12所示，为验证本文算法效果，从TFDS图像库中随机抽取编号为000236的缓解阀盖图像(图12b)，分别对其进行旋转、缩放处理后，计算目标轮廓与原始模板的相似度，计算结果见表1和表2，各计算结果保留5位有效数字。

结合表1和表2数据可以看出，对于缩放和旋转等几何变换，本文算法具有较好的稳定性，缩放变换下的相似值均稳定在0.15以下，平均值为0.113 54，而旋转变换下的相似值整体上偏大，但也稳定在0.2以下，平均值为0.159 76,略大于缩放变换下的平均值。同时观察两种变换下的相似值标准差，旋转变换标准差略大于缩放变换标准差，说明相似值旋转变换下波动较大，即对旋转变换稍敏感，其主要原因是轮廓点集的顺序在旋转变换下会发生细微改变，像素点在映射时会有偏移，导致轮廓有向线段重构时出现细小偏差。

(a)原始模板图(b)缓解阀图像编号000236

(c)缓解阀图像编号00090图12 实验分析图像Fig.12 The images of experimental analysis

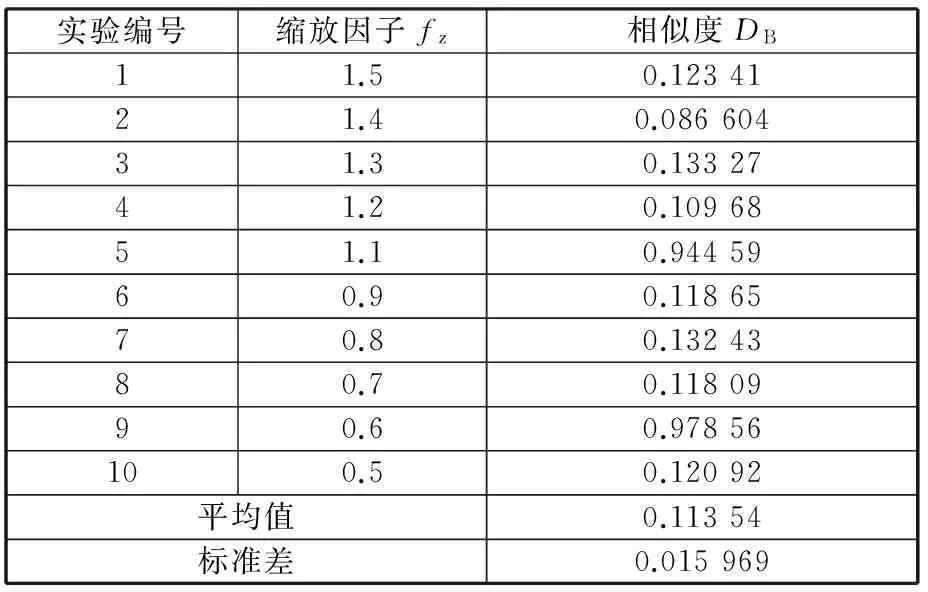
表1 缩放变换下的相似值数据

表2 旋转变换下的相似值数据

为验证本文算法效率，再次从TFDS图像库中随机抽取编号为00090的缓解阀盖图像(图12c)，对其进行一系列旋转和缩放组合变换后，分别计算其轮廓与模板的相似度，每组实验运行10次，取其耗时均值做记录，如表3所示。

表3 组合变换下的算法耗时和相似值

观察表3可得，对于随机抽取的缓解阀盖图像，在缩放和旋转组合变换下算法仍具有良好的适应性。同时注意到编号为1和2的两组实验运行时间较长，其原因主要是目标图像在放大情况下，其轮廓点集容量也会相应扩大，造成算法处理量增大，因此耗时较长。但在实际运用过程中，因TFDS图像采集设备位于轨道旁固定位置[10]，所摄取图像并不会出现大范围的缩放变化，所以本文算法完全能满足TFDS检测的实时性要求。

缓解阀盖匹配识别实验环境为Pentium(R) 3.0GHz，内存4.00GB的PC机，操作系统为32位Windows7，软件平台为VisualStudio2010+OpenCV2.4.9。

5 结论

实验结果表明，本文提出的缓解阀盖匹配识别方法对旋转、平移和缩放等几何变化均具有良好的适应性，基于轮廓动态采样和特征统计数据的匹配能避免特征点选择偏差对匹配结果造成的影响，具有一定的鲁棒性。该方法不仅能满足TFDS缓解阀盖检测的实时性要求，同时也可推广运用于具有不规则外形的盘盖类零件检测。

[1] 吴晓雨, 何彦, 杨磊,等. 基于改进形状上下文特征的二值图像检索[J]. 光学精密工程, 2015, 23(1):302-309.WUXiaoyu,HEYan,YANGLei.BinaryImageRetrievalBasedonImprovedShapeContextAlgorithm[J].OpticsandPrecisionEngineering, 2015, 23(1): 302-309.

[2] 师文, 朱学芳. 基于轮廓重构和特征点弦长的图像检索[J]. 软件学报, 2014(7):1557-1569.SHIWen,ZHUXuefang.ImageRetrievalBasedonContourReconstructionandFeaturePointChordLength[J].JournalofSoftware, 2014(7):1557-1569.

[3] 谭结清. 列车制动系统的性能分析与研究设计[D]. 长沙：中南大学, 2010.TANJieqing.BrakeSystemPerformAnalysisandStudyDesign[D].Changsha:CentralSouthUniversity,2010.

[4] 邹荣, 李健康, 徐家祥,等. 复杂场景下铁路货车锁紧板偏转故障检测[J]. 铁道科学与工程学报, 2015，12(4):917-922.ZOURong,LIJiankang,XUJiaxiang,etal.DeflectionfaultDetectionforLockingPlateofFreightTrainsunderCoMplexScene[J].JournalofRailwayScienceandEngineering, 2015，12(4):917-922.

[5] 袁庆升, 张冬明, 靳国庆,等. 视频检索中图像信息量度量[J]. 通信学报, 2016, 37(2):80-87.YUANQingsheng,ZHANGDongming,JINGuoqing,etal.ImageInformationMeasurementforVideoRetrieval[J].JournalonCommunications, 2016, 37(2):80-87.

[6] 孙思远, 陈莉, 廖鸿森. 基于二维直方图图像智能分割的体绘制传递函数设计[J]. 计算机辅助设计与图形学学报, 2014, 26(10):1583-1592.SUNSiyuan,CHENLi,LIAOHongsen.TransferFunctionDesignfor3DVolumeRenderingBasedonIntelligent2DHistogramImageSegmentation[J].JournalofComputer-AidedDesignandComputerGraphics, 2014, 26(10):1583-1592.

[7]TOMASIC,MANDUCHIR.BilateralFilteringforGrayandColorImages[C]//InternationalConferenceonComputerVision.Bombay,India:IEEE,1998:839-846.

[8]IIVARINENJ,VISAA.ShapeRecognitionofIrregularObjects[J].ProceedingsofSPIE—theInternationalSocietyforOpticalEngineering, 1999, 2904:25-32.

[9] 孙国栋, 徐威, 梁永强,等. 基于形状上下文的列车挡键丢失图像识别算法[J]. 铁道科学与工程学报, 2014,11(6):127-131.SUNGuodong,XUWei,LIANGYongqiang,etal.ImageRecognitionAlgorithmforSideFrameKeyofTrainBasedonShapeContext[J].JournalofRailwayScienceandEngineering, 2014,11(6):127-131.

[10] 曾霖. 图像拼接技术的研究、实现与应用[D].武汉： 武汉大学, 2012.ZENGLin.Research,ImplementationandApplicationofImageMosaic[D].Wuhan：WuhanUniversity,2012.

(编辑 苏卫国)

Image Matching Algorithm of Release Valve Bonnet Based on Contours Reconstructed by Oriented Line Segments and Pairwise Geometrical Histogram

ZHAO Daxing WANG Bo ZHOU Weiti SUN Guodong

School of Mechanical Engineering,Hubei University of Technology，Wuhan， 430068

For the missing faults of release valve bonnets in freight cars, an image matching algorithm was proposed herein based on contour reconstructed by oriented line segment and pairwise geometrical histogram. Firstly, the location of initial sampling point was defined by maximum chord length and polar radius, then the contour was dynamically and hierarchically sampled according to an evaluation mechanism of local curvatures. Then adjacent sample points were lined in counter-clockwise order, oriented relative angles and normalized equivalent distances between pairwise oriented line segment were calculated as the dual descriptors, which were counted into the two dimensional histogram. Finally the similarity between histograms was measured by Bhattacharyya distance. The experimental results show that the algorithm may keep robust under the circumstances of rotations, scales and translations, meanwhile the detection efficiency is also well ensured, which may satisfy the instantaneity of the detection on freight cars.

release valve bonnet; matching; oriented line segment; pairwise geometrical histogram

2016-10-10

国家自然科学基金资助项目(51675166，51205115)

TP29

10.3969/j.issn.1004-132X.2017.06.014

赵大兴，男，1962年生。湖北工业大学机械工程学院院长、教授、博士研究生导师。研究方向为无损检测与机器视觉。王 博，男，1990年生。湖北工业大学机械工程学院硕士研究生。E-mail:ssgestapo@126.com。周唯倜，男，1994年生。湖北工业大学机械工程学院硕士研究生。孙国栋，男，1981年生。湖北工业大学机械工程学院副教授、博士。