跳扩散模型下具有信用风险的亚式期权定价
展瑜萌,李翠香
(河北师范大学 数学与信息科学学院,河北 石家庄 050024)
跳扩散模型下具有信用风险的亚式期权定价
展瑜萌,李翠香*
(河北师范大学 数学与信息科学学院,河北 石家庄 050024)
假设期权的标的资产服从几何布朗运动,交易对手公司价值服从跳扩散模型,利用测度变换的方法,推导了具有信用风险的连续几何平均亚式看涨与看跌期权的定价公式.
信用风险;亚式期权;跳扩散模型;测度变换
0 引言
期权[1]是一种衍生金融工具,随着金融理论的发展和市场的需求,人们在标准期权的基础上设计出了许多新型期权.亚式期权[2]就是其中一种具有路径依赖性的新型期权,其价值取决于期权到期日前一段时间内或整个期权期限内标的资产价格的平均值.相对于普通欧式期权,亚式期权的价值通常具有较小的波动性,因此受到了投资者的广泛关注.信用风险也就是违约风险,是指由于合约另一方未履行合约订立的义务而导致债券人发生经济损失的可能性.随着期权在场外交易市场的交易量日渐上升,其遭受到信用风险的可能性增大,并且现实中标的资产价格不一定是连续的,其价格可能会因为某些重大事件(如金融危机、自然灾害等)的出现而发生间断性的跳跃,研究跳扩散模型下的期权定价更具有现实意义,因此本文将考虑跳扩散模型下具有信用风险的几何平均亚式期权的定价.

c(ST,T)=[GT-K]+(1{VT≥L}+θ(T)1{VT p(ST,T)=[K-GT]+(1{VT≥L}+θ(T)1{VT 以下假设市场是均衡的,完备的,无套利存在,并且Vt,St分别服从如下SDE (1) (2) Ep[X]=EQ[Λ(T)X], 其中E[·]表示期望. 在证明跳扩散模型下具有信用风险的亚式期权定价之前首先证明下面两个引理. 引理2.1 设 其中 证明 利用伊藤积分的分部积分公式[4]可知 其中 (3) 从而 (4) (5) 从而 (6) 由全期望公式知 (7) 因为 (8) (9) Q1(XT>A,YT>B|N(T)=n)=N2(dn,d;ρn). (10) 联合(3)(7)(10),引理2.1得证. 引理2.2 在引理2.1的条件下,若ZT改为 则 其中ρn由引理2.1给出, 证明 类似于(2.3)并由分部积分公式可得 (11) 其中 EQ[ZT1{XT>A,YT>B}]=Z0eDEQ2[1{XT>A,YT>B}], (12) 且由引理1.2知 (13) 类似引理2.1的证明可得 (14) 将(14)代入(12)可知引理2.2得证. 定理2.1 设Vt,St分别服从SDE(1),(2),则到期日为T,执行价格为K的具有信用风险的几何平均亚式看涨期权在0时刻的价格为 其中 证明 由风险中性定价原理知 c(S0,0)=e-rTEQ[c(ST,T)]=e-rTEQ[GT1{VT≥L,GT>K}]-Ke-rTEQ[1{VT≥L,GT>K}]+ (15) 解SDE(1),(2)可得 (16) (17) 在引理2.1中,取XT=VT,YT=GT,ZT=GT得 (18) 在引理2.1中,取XT=VT,YT=GT,ZT=0得 (19) 由(16)(17)可得 在引理2.2中,取XT=VT,YT=GT,ZT=GTVT得 (20) 在引理2.2中,取XT=VT,YT=GT,ZT=VT得 (21) 由(15),(18)-(21)可知,定理2.1得证. 类似定理2.1的证明可得下面定理2.2. 定理2.2 在定理2.1的条件下,具有信用风险的连续几何平均亚式看跌期权在0时刻的价格为 本文在标的资产服从几何布朗运动,交易对手公司资产服从跳扩散过程,公司负债为常数的情况下利用测度变换的方法和风险中性定价原理研究了具有信用风险的亚式期权定价.给出了具有信用风险的连续几何平均亚式看涨,看跌期权在0时刻的价格.当N(t)=0时,交易对手公司服从几何布朗运动,很容易看出跳扩散过程富含了几何布朗运动和不规则的跳跃,因此这种假设更具有现实意义. [1] John C.Hull.Option futures and other derivatives[M].北京:机械工业出版社,2011:138-243. [2] Peter G.Zhang.Exotic options[M].北京:机械工业出版社,2014:75-81. [3] M.K.Kwok.Mathematical models of financial derivatives[M].Berlin: Spinger Press,2008:188-200. [4] Fima C.Klebaner.Introduction to Stochastic Calculus with Applications[M].北京:人民邮电出版社,2008:267-280. [5] 李翠香,石凌.基于随机利率下跳-扩散过程的复合期权定价[J].黑龙江大学学报:自然科学版,2012,29(4):431-436. [6] 姜博.几何平均亚式期权的定价及参数敏感性分析[D].石家庄:河北师范大学,2014. (责任编辑 郑绥乾) Pricing of Asian Options with Default Risks Under Jump-diffusion Models ZHAN Yu-meng,LI Cui-xiang* (CollegeofMathematicsandInformationScienceofHebeiNormalUniversity,Shijiazhuang050024,China) In this paper,we assume the underlying asset prices follow Geometric Brownian process,and the asset value of the counterparty company follow jump-diffusion models.By the help of changing measures,we derive the analytical formulas of continuous geometric average Asian call and put options with default risks. default risk;asian option;jump-diffusion models;measure transform 2016-12-15 国家自然科学基金(11401159) 展瑜萌(1991-),女,硕士,研究方向:概率与数理统计,E-mail:1530040347@qq.com. *通讯作者:李翠香(1971-),女,博士,教授,研究方向:金融数学,E-mail:cuixiang_li@126.com. O 211.6 A 1000-5846(2017)01-0009-06
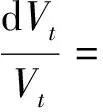


1 预备知识


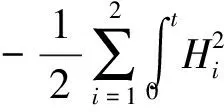



2 跳扩散模型下具有信用风险的亚式期权定价





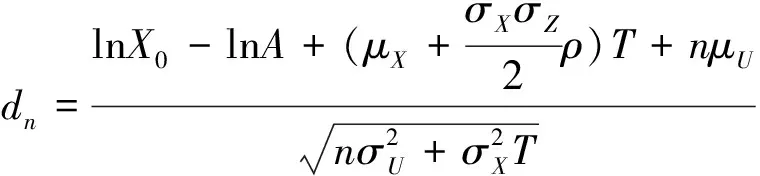




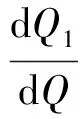












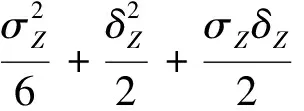

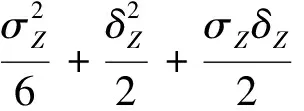
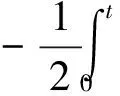



















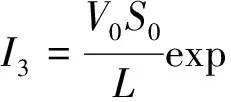




3 总结

