基于SVD分解的主成分分析人脸识别方法

程浩男

摘 要 人脸识别一直是模式识别中的热门问题，而主成分分析又是其中的主流方法之一。这里我们用随机过程的观点去看待一个灰度图像，每个像素中有随机性的存在，也有人脸之间的类内差别，但人脸区别于其他图片，有自己专属于这一类随机过程的特点。我们采用基于SVD的主成分分析，将人脸的主成分提取出并用测试集测试其准确度。之后，并采用特征值分解的方法大大提高效率且不改变实验结果。

关键词 人脸识别；主成分分析；奇异值分解；特征值分解

中图分类号 TP3 文献标识码 A 文章编号 1674-6708（2017）179-0040-02

随着人工智能的飞速发展，人脸识别吸引了越来越多的关注及研究。主成分分析因为其方便简单的特点成为比较常用的方法之一，而SVD分解又成为主成分分析中的主流实现方法，但该方法有一定缺陷，比如处理大矩阵效率较低。为了得到更高效率的主成分分析方法，越来越多的工作者开始研究如何提高主成分分析的效率。

经过研究，当矩阵的两个维度相差很大时，将矩阵与其转置相乘得到相关矩阵，即一个维度较小的矩阵，再求其特征值与特征向量能够得到与直接进行SVD分解相同的结果，而上述相关矩阵求特征值的替代方法却能极大地提高效率。

第二节将详细介绍基于SVD的主成分分析和基于特征值分解的替代算法的基本原理。第三节将详细介绍的两种方法对应的实验步骤。第四节将详细比较这两种方法的异同，主要是算法耗费时间的差异。第五节总结根据我们设计的实验得到的结论。

1 基本原理

主成分分析的主要思想是提取出训练集中图片的主成分，使测试集与其主成分做内积观察结果，进而将人脸图片与其他图片相区别。

我们将训练集的图片读入，并将每一张图片都拉成“一条向量”放在一个矩阵的一行中，减去平均值，此时的图像矩阵示意图如下：

我们的数据集共有35个图片，图片拉长之后的向量长为108×75=8 100，故矩阵的行数为8 100，列数为35。可知这是一个行列维度相差很多的矩阵。

1.1 基于SVD的主成分分析

奇异值分解是主成分分析的主流方法，其原理在于将原矩阵P分解为3个矩阵相乘：

U×S×V=P

其中U和V是单位正交矩阵，S是对角阵。通过这样的分解，我们得到U和V代表两个维度上的主成分，而S的对角元素代表对应主成分的重要程度。在本实验中，V的每一行有着明确的物理意义，代表图片的主成分。

1.2 基于相關矩阵特征值分解的快速算法

当需要奇异值分解的矩阵在两个维度上相差较大时，我们可以用相关矩阵特征值求解的办法来提高计算效率，并且得到相同的结果。首先我们需要得到P的相关矩阵R：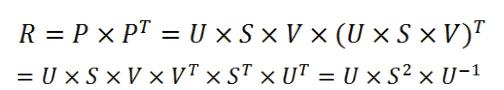

然后，将奇异值分解的结果带入相关矩阵，由于正交阵的转置即是它自身的逆，故不难发现经过推倒得到了特征值分解的形式，所以我们仅需要做特征值分解的计算即可得到奇异值分解中的S和U矩 阵。

至此，我们用相关矩阵求特征值分解的方法已经完全求出奇异值分解的结果。

2 实验方法

训练集由35张人脸的灰度图像构成，如图2：

测试集如图3：

实验过程由matlab仿真进行。首先，我们将训练集的图片读入，并将每一张图片都拉成“一条向量”放在一个矩阵的一行中，减去平均值，待后续处理。在传统的方法中，我们对该矩阵进行SVD分解，但由于两个维度相差过大，导致较大的维度上的值相对很小，故而在正规奇异值分解算法中浪费了很多时间，而这也正是SVD分解算法效率较低的关键。实验中，我们就传统算法和相关矩阵的特征值算法进行了讨论。继而，我们对SVD的中间的对角阵观察对角元素，可知最大项约为次大项的一倍，故可知在后续的分类中，只需考虑最大项对应的主成分。在训练集输入完成以后，我们将待检测图片按照同样的方法拉成“一条向量”，再与最大主成分求相关系数，即直接做内积并与前面图片作比较即可，可知人脸和马脸图片的运算结果相差一个数量级，故而得以区分。

3 实验结果

在上述实验过程中，将矩阵分解为U×S×V，左右两个矩阵为标准正交阵，中间是对角阵。观察对角阵元素见图4。

可知第一个项是第二个2倍左右，相差较多，故我们可以重点区分以是否像第一个主成分作为判别标准。即第一项可以被看作人脸图像的最主要成分。我们将第一主成分经过线性放缩到0到255灰度值区间并可视化观察，如图5左，可以看作是一个近似每张人脸平均的这样一个结果。而实际上排序相对靠后地主成分也有特定地物理含义，例如第4个主成分，如图5右，主要表征了肩上头发的多少的区别。

我们用主成分去和测试集地人脸图片和马脸图片分别作内积，得到图6。可明显观察到，测试集人脸图片和上面分析的主成分进行内积明显高于测试集马脸地内积结果。我们根据图中观察可得出将2 000设为判定是否为人脸地阈值：即当内积值大于或等于2 000，我们把测试图片判定为人脸，若内积值小于2 000，我们把测试图片判定为非人脸。

4 算法对比

我们经过原理分析和实验结果均证明两种方法得到的结果完全相同。但是两者的耗费时间却相差很多，我们在matlab上进行试验，对比运行时间发现，传统SVD方法耗时约2.7S，而我们的基于特征值分解的快速替代算法耗时约0.0026S，效率提高了大约1 000倍。这在大量级数据集上将发挥着至关重要的作用。

5 结论

基于SVD主成分分析人脸识别方法是一种简单可靠的方法，能够得到很清晰的分类效果。而其效率较低地问题在待分解矩阵维度相差较大情况下可以通过特征值分解的方式，在保证得到相同结果的前提下，大大提高算法运行效率。

参考文献

[1]何婧，冯国灿.奇异值分解在人脸识别中的应用[J].广东第二师范学院学报，2006，26（3）：92-96.

[2]罗小桂.矩阵奇异值分解（SVD）的应用[J].井冈山医专学报，2005，12（4）：133-135.

[3]梁毅雄，龚卫国，潘英俊，等.基于奇异值分解的人脸识别方法[J].光学精密工程，2004，12（5）：543-549.

[4]庞彦伟，刘政凯，俞能海.融合奇异值分解和主分量分析的人脸识别算法[J].信号处理，2005，21（2）：202-205.

[5]牟雪娇.奇异值分解和主成分分析在车型识别中的应用[D].上海：上海交通大学，2008.