高阶紧密交替符号补矩阵的秩的算法
张 容,邵燕灵
(中北大学 理学院, 太原 030051)
高阶紧密交替符号补矩阵的秩的算法
张 容,邵燕灵
(中北大学 理学院, 太原 030051)
定义了紧密交替符号矩阵的补矩阵,利用矩阵的初等变换,研究了该矩阵秩的求解过程。最后,当n≥5k时,提出了该矩阵的秩的计算算法,并给出了一个实例验证了算法的可行性。
紧密交替符号矩阵;补矩阵;秩的算法
一个符号模式矩阵(符号矩阵)是一个元素取自于集合{+1,-1,0}的矩阵。
定义1 一个交替符号矩阵,是指一个没有完全零行和零列的,其元素取自于集合{+1,-1,0}的方阵,并且满足在任一行和任一列之中+1和-1交替出现,开始和最后出现的都是+1[1]。
定义2 一个矩阵被称为紧密的(行紧密、列紧密),是指在这个矩阵的每条线(行、列)上没有零元素存在于2个非零元素间[2]。


1983年,Mill等在交替符号矩阵的猜想[3]引起了以Brualdi、Kim等学者在此方面的研究兴趣[4-8]。文献[1]研究了0-非0模式的n阶交替符号矩阵,文献[2]研究了紧密交替符号矩阵与完全幺模矩阵、组合矩阵和广义互补基本矩阵的关系,文献[7]得到了一个n阶交替符号矩阵的最大谱半径,文献[8]得到了一类交替符号矩阵的逆和广义逆。2015年,Fiedler等在文献[9]中得到了紧密交替符号矩阵的秩的计算公式。
低阶Bn,k的秩通常易得,而本文主要研究高阶Bn,k的秩的算法。
1 预备知识
用Jn表示n阶全1矩阵(在不引起混淆的情况下,简记为J),用An,k表示将En,k中的所有非零元素全替换为1后所产生的(0,1)矩阵,用Fn,k表示将An,k中的(1,k-1),(2,k-2),…,(k-1,1)元素全部替换为1后产生的矩阵,例如:
引理1[9]记(a,b) 代表整数a和整数b的最大公约数,r(M)及v(M)分别表示一个矩阵M的秩及零度,则
由秩-零化度定理可得:r(M)+v(M)=n。下面推论是显然的:




引理1~3给出r(Bn,k)的一个估计。下面为计算r(Bn,k)方便,引入Cm、Dn,k。





若k=1,Bn,k为一个对角元为0其余元素均为1的矩阵,即Bn,1=Jn-In,则这样的矩阵显然是非奇异的,有r(Bn,k)=n。故以下讨论默认k>1。
引理4 当n≥5k时,r(Bn,k)=3k-1+r(Dn-3k+1,k)。
证明 对Bn,k进行一系列初等变换后易得如下结果:
对Cm依次作如下初等变换:
1) 将Cm的第k-1-i列的-1倍加到Cm的第k-1+i列,i=1,2,…,k-2;
2) 将Cm的第k-1-i行的-1倍加到Cm的第k-1+i行,i=1,2,…,k-2;
3) 对Cm前k-2行进行初等行变换,化为反向负单位矩阵;
4) 将Cm的第k-1列的-1倍加到Cm的第2k-2+i列,i=1,2,…,n-4k+2。

2 高阶r(Bn,k)算法
由于低阶Bn,k的秩容易得到,认为n≥5k时n相对较大,下面对n≥5k时Bn,k的秩的算法进行研究。由引理4知r(Bn,k)=3k-1+r(Dn-3k+1,k),故下面仅给出计算r(Dn-3k+1,k)的算法步骤:
步骤1 为计算方便,记p=n-3k+1,Dn-3k+1,k=Dp,k。首先对Dp,k进行判别,因p≥2k+1,故一定存在一个正整数α使得0≤p-α(2k-1) 1) 若α满足0≤p-α(2k-1) 其中(α-1)I2k-1代表的是(α-1)个I2k-1矩阵块。此时,r(Dp,k)=(α-1)·(2k-1)+(k-1)+r(αAp-(α-1)(2k-1)-(k-1),k+J),接下来进行步骤2。 2) 若α满足k≤p-(α-1)(2k-1)<2k-1,则说明Dp,k通过一系列初等变化,可得到: 此时r(Dp,k)=(α-1)·(2k-1)+r(αFp-(α-1)(2k-1),k+V),接下来则跳过步骤2,直接进行步骤3。 步骤2 首先,将αAp-(α-1)(2k-1)-(k-1),k+J这种形式重新看成αAq,u+J(q,u∈Z+)来计算。 步骤3 将αFn-(α-1)(2k-1),k+V这种形式看成αFq,u+V(q,u∈Z+)来计算。 2) 若u 通过上述步骤,由步骤1判别后进行步骤2和步骤3的相互迭代即可求得相应的r(Dn-3k+1,k),由引理4可求得r(Bn,k)。 计算B77,11的秩。 本文定义了紧密交替符号模式补矩阵Bn,k,当n≥5k时,提出了秩的计算算法。同时,由于Bn,k和Bn,n-k+1通过列的逆序排列可相互得到,有r(Bn,k)=r(Bn,n-k+1),故解决了Bn,k对应低阶时的秩。 [1] BRUALDI R A,KIERNAN K P,MEYER S A,et al.Patterns of alternating sign matrices[J].Linear Algebra & Its Applications,2013,438(10):3967-3990. [2] FIEDLER M,HALL F J,STROEV M.Dense alternating sign matrices and extensions[J].Linear Algebra & Its Applications,2014,444:219-226. [3] MILLS W H,ROBBINS D P,JR H R.Alternating sign matrices and descending plane partitions[J].Journal of Combinatorial Theory,1983,34(3):340-359. [4] BRUALDI R A,KIM H K.Completions of Alternating Sign Matrices[J].Graphs & Combinatorics,2015,31(3):507-522. [5] BRUALDI R A,KIM H K.A Generalization of Alternating Sign Matrices[J].Journal of Combinatorial Designs,2015,23(5):204-215. [6] BRUALDI R A,KIM H K.Symmetric alternating sign matrices[J].2014,60(3):333-345. [7] BRUALDI R A,COOPER J.Note on the spectral radius of alternating sign matrices[J].Linear Algebra & Its Applications,2014,442(442):99-105. [8] CATRAL M,LIN M,OLESKY D D,et al.Inverses and eigenvalues of diamondalternating sign matrices[J].Special Matrices,2014,2(1):78-84. [9] FIEDLER M,GAO W,HALL F J,et al.Ranks of dense alternating sign matrices and their sign patterns[J].Linear Algebra & Its Applications,2015,471:109-121. [10]HORN R A,JOHNSON C R.Matrix Analysis(Second Edition)[M].Beijing:China Machine press,2014. (责任编辑 陈 艳) Algorithm for Rank of High Order Dense Alternating Sign Complement Matrices ZHANG Rong, SHAO Yan-ling (School of Science, North University of China, Taiyuan 030051, China) The defination of dense alternating sign complement matrices was proposed and the solving process of the rank of this matrices was researched by elementary operation. Finally,whenn≥5k,we give a calculation algorithm for rank and provide a practical example to verify the feasibility of the algorithm. dense alternating sign matrices; complement matrix; algorithm for rank 2016-10-28 基金项目:国家自然科学基金资助项目(11071227);山西省回国留学人员科研资助项目(12-070) 张容(1992—),女,硕士硕士生,主要从事组合数学研究,E-mail:rena345@163.com ;通讯作者 邵燕灵,女,博士,教授,主要从事组合数学研究。 张容,邵燕灵.高阶紧密交替符号补矩阵的秩的算法[J].重庆理工大学学报(自然科学),2017(3):175-180. format:ZHANG Rong, SHAO Yan-ling.Algorithm for Rank of High Order Dense Alternating Sign Complement Matrices[J].Journal of Chongqing University of Technology(Natural Science),2017(3):175-180. 10.3969/j.issn.1674-8425(z).2017.03.027 O157 A 1674-8425(2017)03-0175-06

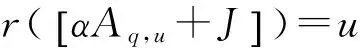





3 算法实例
4 结束语

