例谈“设且求”思想在解题中的应用
广东省兴宁市第一中学(514500) 蓝云波
例谈“设且求”思想在解题中的应用
广东省兴宁市第一中学(514500) 蓝云波
在高中数学中,“设而不求”是非常重要的一种数学思想,这种思想方法是在解题过程中,由于要使用到某个方程的根,但却并不直接求出,而是通过设出未知数,并借助一定的手段进行消元或代换的一种思想方法.这个设出的未知数起到非常重要的桥梁作用.笔者在教学过程中发现,这种思想方法主要应用在导数与解析几何中.虽然这种思想方法具有重要的价值,但从解题的角度讲,这是一种迂回曲折的方法.学生在学习的过程中,也曾提问过笔者,对通常涉及二次方程的设而不求问题,是否一定要借助设而不求的思想,如果可以不使用这种方法,如何突破解题的瓶颈.这个问题引起了笔者的注意,于是从求根的视角重新审视了这类问题.由于使用二次方程的求根公式求出的根较为复杂,是“暴力”地求出方程的根,可称作“设且求”思想.现笔者从导数和解析几何方面作一些探索,现分析如下,供大家参考.
一、导数中的应用
某些函数的极值问题,求导之后发现极值点是二次方程的根,但此二次方程的根较为复杂,只能用求根公式求解.笔者发现,常见的做法并不是使用求根公式求出二次方程的根,因为方程的根显得较为复杂,似乎不利于问题的求解,常见的做法仍然是设而不求或分类讨论.笔者发现,这类问题,使用求根公式也是一种通法,关键在于实施计算强行求解,或借助换元,发掘新的未知数与参数的关系式,然后利用整体代换的思想并构造新的函数进行分析,此时问题可能反而变得简单.
例1设函数(a∈R).
(1)若f(x)在x=0处取得极值,确定a的值,并求此时曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若f(x)在[3,+∞)上为减函数,求a的取值范围.
解析(1)略;(2)

方程-3x2+(6-a)x+a=0的判别式

令f′(x)=0得,
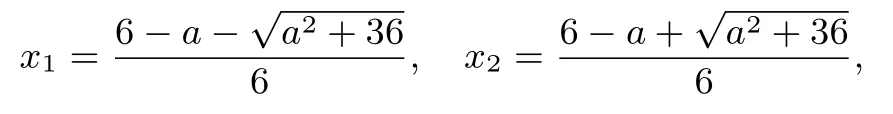
且x1< x2.当x∈(-∞,x1)时,f′(x)< 0,f(x)单调递减;当x∈(x1,x2)时,f′(x)> 0,f(x)单调递增;当x∈(x2,+∞)时,f′(x)<0,f(x)单调递减.所以函数f(x)的减区间为(-∞,x1]和[x2,+∞).要使f(x)在[3,+∞)上为减函数,则必有x2≤3,即,解得a≥-.所以a的取值范围为.
点评本题在求出导函数之后,可转化为二次方程-3x2+(6-a)x+a=0在(3,+∞)上没有实根,并借助根的分布,通过设而不求和二次方程的根的分布解决.而本文给出的解法,直接“暴力”求出实根,通过强行计算解答,整个过程相当直观且易于理解,干净利索并具有直捣黄龙之妙!且运算并不复杂,是一种自然的解法.
例2已知函数f(x)=lnx-ax2+x,a∈R.
(1)求函数f(x)的单调区间;
(2)是否存在实数a,使得函数f(x)的极大值大于0.若存在,求出a的值;若不存在,请说明理由.
解析(1)略;
(2)由(1)可知,f(x)有极值,则a>0且f(x)有极大值无极小值,

点评本题也是导数零点不可求题型,参考答案是用比较复杂的设而不求的思想方法解答的.实际上,本题的导函数的零点可用二次方程的求根公式直接求出,虽然表面上看起来很复杂,但通过发掘根与参数的关系,利用整体换元,并限定出t的范围,可构造一个较为简单的函数解决,反而有四两拨千斤之妙!
例3已知函数.
(1)当a=-4时,试判断函数f(x)在(-4,+∞)上的单调性;
(2)若函数f(x)在x=t处取到极小值.
①求实数t的取值集合T;
解析(1)略;(2)①略;②

因为且函数f(x)在x=t处取到极小值,所以t2-at-a=0,且Δ=a2+4a>0,结合a<0,解得a<-4.所以

点评本题与例1是类型题,但更为复杂,“暴力”求根的美感及精妙之处显露无疑.笔者发现,求根公式在求解这类导数零点不可求问题时具有一定的通性通法.原来解题还有这样的快感!
二、解析几何中的应用
设而不求是解析几何的最常用的技巧,其重要性不言而喻.在涉及直线与圆锥曲线的综合解答题中,这种策略尤其显得如鱼得水.但是,反其道而行之,未尝不可,设且求实际上也是一种有效的解决解析几何问题的重要手段,有时会达到意想不到的效果.而这种方法普遍被大部分人所忽视.下面让我们再次感受一下“暴力”求根法的威力.
例4已知焦点在x轴上的椭圆E:=1内含圆C:x2+y2=.圆C切线l与椭圆E交于A,B两点,满足.
(1)求b2的值;
(2)求|AB|的取值范围.
解析: 依题意知直线OA,OB的斜率均存在,设A(xA,yA)为第一象限的点,直线OA的方程为y=kx,联立.所以有xA=.令
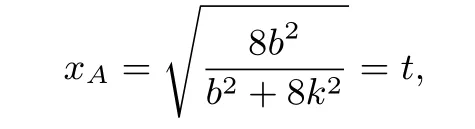
则yA=kt.设B(xB,yB).则


即8b2(1+k2)=(8+b2)(1+k2).因为1+k2/=0,所以8b2=(8+b2),即b2=4.易验证当k不存在时,也满足b2=4.点A在其它象限时,同理可解得b2=4.
(2)由(1)得


点评通过分析发现,直线与曲线的交点坐标并不难求,若能用设且求的思想,并以换元法为武器,可提高解题效率.笔者发现,这种设且求的思想被很多人忽视,被认为运算复杂,不利于问题的解决.这其实是值得商榷的.本题通过“暴力”求根,利用换元思想,运算并不复杂,甚至比用设而不求的方法简单得多.这说明,若能走出思维的牢笼,则能实现方法的创新.
例5如图,在平面直角坐标系 xOy中,椭圆=1(a>b>0)的右焦点F(1,0),离心率为.分别过O,F的两条弦AB,CD相交于点E(异于A,C两点),且 OE=EF.

图1
(1)求椭圆的方程;
(2)求证:直线AC,BD的斜率之和为定值.
解析(1)略;
(2)由OE=EF可得∠EOF=∠EFO,所以直线AB与直线CD的斜率互为相反数,设AB的方程为y=kx,直线CD的方程为y=-k(x-1).联立



点评本题通过“暴力”求根,借助换元思想,完全走出了思维的牢笼,使我们再次见识了这种思想方法的威力!
通过以上的分析,我们认识到,对于有些问题,虽然已经有常见的通法存在,但鉴于其局限性与数学思想方法的多样性,还可从其他角度解决问题.这说明,我们在研究问题时,不能固步自封,思维定势,以致禁锢了自己的思维.若能打破固有的僵化思维,则能实现方法的创新.而这种创新思维则是我们最需要在教学过程中培养和传授给学生的.而且这种创新的思维,对于提高教师教学的有效性具有不可估量的作用,而且对学生的成长与发展具有深远的意义.

