利用奇异函数法对轻型卡车纵梁弯曲刚度分析

左印波，孙江平，蔡欣

（安徽江淮汽车集团股份有限公司，安徽 合肥 230601）

利用奇异函数法对轻型卡车纵梁弯曲刚度分析

左印波，孙江平，蔡欣

（安徽江淮汽车集团股份有限公司，安徽 合肥 230601）

基于奇异函数法，并结合单位载荷法，推导出在一般受力状态下的轻型卡车纵梁挠曲通用方程，用于求解车架纵梁最大挠度，进行弯曲刚度校核。

奇异函数；纵梁；挠曲方程；单位载荷；弯曲刚度

CLC NO.: U467.3 Document Code: A Article ID: 1671-7988 (2017)05-54-03

引言

轻型卡车的车架纵梁是车辆主要承载元件，承受安装在其上面的各种装置、人员和货物的重量以及来自悬架系统的反作用力，因此须对纵梁进行弯曲刚度分析。

传统的车架纵梁挠度的计算方法是在车架纵梁不同荷载、截面变参数等处分段，分别建立挠度方程，再联立相邻段的位移边界条件来求解。当所受载荷复杂或纵梁为变截面、弯纵梁时，这种方法十分烦琐整个过程烦琐，边界条件多。而利用奇异函数来求解，可以建立计算方程进行统一表达，从而能够求解上得到很大的简化，并且利于编程，利用计算机进行求解。

在进入20世纪90年代后，我国一些学者把奇异函数用于力学问题的求解[1-3]，但在汽车车架纵梁上的分析上的应用却极少，有学者利用奇异函数仅对特定的变截面直纵梁强度分析进行了初步尝试[4]。

本文基于奇异函数法，并结合单位载荷法，针对轻型载货汽车常用的直纵梁、弯纵梁、变截面梁等车架纵梁，推导出统一挠曲方程，可精确计算出各点挠度及最大挠度，进行纵梁弯曲刚度分析。

1、奇异函数的定义

奇异函数又称麦考利函数，是一个由多项奇异函数构成的函数族，由下式给出[1]：

当n≥0时，

当n＜0时，

当n=0时称为单位阶跃函数，n=-l时称为δ函数，这里n为整数，它的基本微分为：

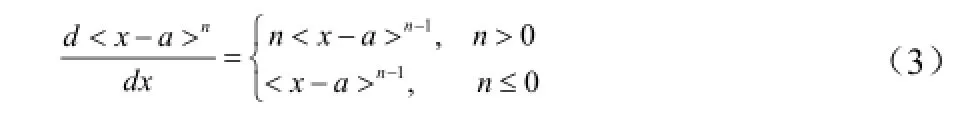
奇异函数的积分为：

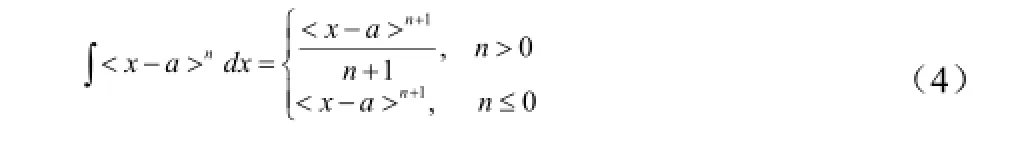
2、利用奇异函数表达常见载荷及刚度

车架纵梁常见的受力情况及刚度变化，可用如下奇异函数表达[5]。

（1）作用在x=ai处的集中力偶Mi可表达为：（2）作用在x=bj处的集中力Pj可表达为：

（3）作用于（ck,dk）处的均布线载荷qk可表达为：

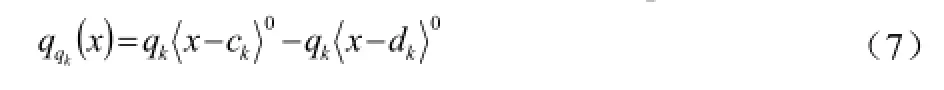
抗弯刚度EI沿整个构件长度方向发生阶形变化,截面抗弯刚度EI发生t次，另t次的抗弯刚度的倒数(即柔度)的改变量βt称为变柔度系数[6-7]，则有：

由式（8）可以写出受弯构件的变参数（抗弯刚度EI发生改变）对构件的影响[5]：

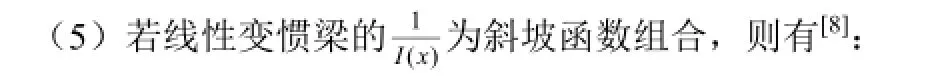
3、基于奇异函数的弯曲刚度分析

本文以计算难度较大的变截面弯纵梁为基础建立通用挠曲方程。

将轻型卡车前后悬架与车架纵梁相互作用力，简化为支撑纵梁的支座，简化后纵梁的受力情况如下：

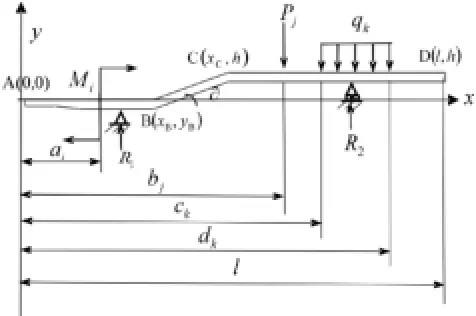
图1 变截面弯纵梁受力示意图

其中：

A（0，0）—车架纵梁最前端；

B（xB，yB）—车架纵梁前拐点；

C（xc，yc）—车架纵梁后拐点；

l—车架纵梁沿x轴方向长度；

h—为车架上表面前后y方向高度落差；

D（l, h）—车架纵梁最后端；

R2—车架纵梁支座反力，坐标位置为(xR2,h)；

Pj、qk力的方向均为垂直于X轴；

∂—车架纵梁折弯角度，00≤∂＜900。

图1表示变截面弯纵梁在x、y坐标下的受力情况，依据奇异函数的定义及性质，可以写出作用在梁上沿x轴分布的等效载荷集度为：

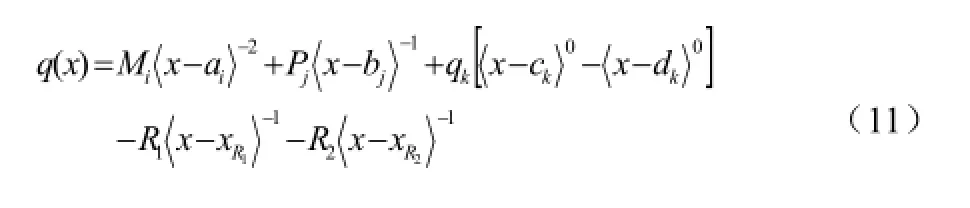
利用截面法，发现在图1所示的x、y坐标及载荷下（Pj、qk力的方向均为垂直于x轴），无论是在纵梁直断还是折弯段所受的弯矩均与x轴坐标相关，对（11）式利用（4）公式，进行积分两次有如下弯矩方程[4,7]：

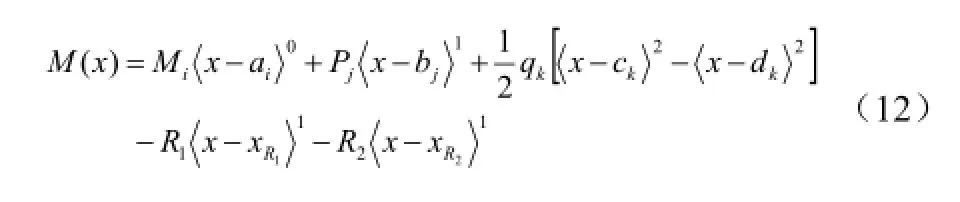
如果梁上作用有L个集中力偶、M个集中载荷、N个均布载荷，则有如下弯矩方程：

其中，支座反力R1、R2可以通过力的平衡方程求出。

计算节点CPU支持AVX-512指令集，大幅度提升了处理器的浮点运算能力，GPU节点采用最新的NVIDIA Tesla V100型号GPU，并采用NVLink方式连接，单卡GPU双精度浮点运算速度理论值可达7.8TFLOPS。计算网络采用omni-path架构，安装有intel、gcc等编译器，作业管理采用slurm调度系统，集群管理采用计算中心自主开发的集群监控管理套件。

纵梁中心线实为双折线，纵梁挠度计算需要沿纵梁中心线路径积分，若用截面法分段处理，进行受力分析，建立挠度方程，边界情况复杂，工作繁琐。为简化工作量，本文依据虚功原理，引入单位载荷法求解车架纵梁各点的挠度。

在纵梁上任意一点E点（xE,yE），施加垂直于纵梁轴线方向的单位力，依据单位载荷法[9]则有：

其中：

I(x)—车架纵梁惯性距变化函数。

单位载荷法计算时纵梁虚拟受力，存在如图3、图4两种情况所示。

图3 在AB或CD段施加单位载荷受力状态

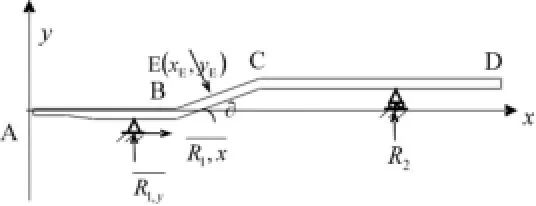
图4 在BC段施加单位载荷受力状态

利用奇异函数通用方程（13）及力的平衡方程，可以求出两种状态下的弯矩方程。

依据奇异函数可将上述两种情况整合，则有：

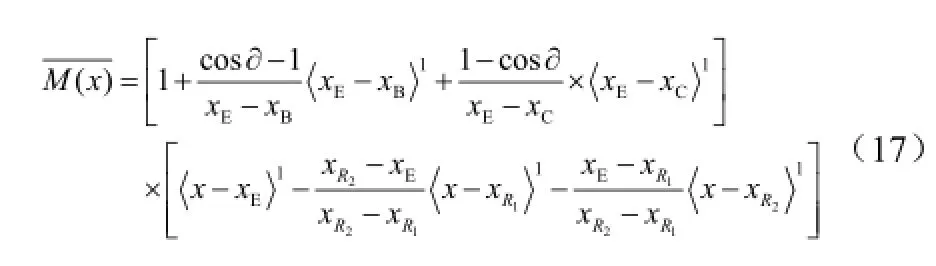
常见的汽车纵梁惯性距变化往往为以下两种惯性距变化的组合：

阶梯梁：其变化函数表达见（8）～（9）公式；

线性变惯距梁：其变化函数见（10）公式。这里简化起见令纵梁惯性距函数为I(x)，实际计算时分别带入（8）～（10），利用奇异函数的定义及性质进行计算，不单独展开。

依据微分原理，ds与dx存在以下微分关系：

将公式（14）进一步拓展，则有如下计算：

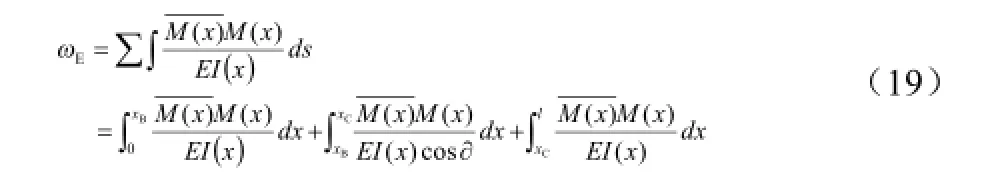
将（13）、（17）公式以及实际的I(x)函数组合公式带入公式（19）中，即可求出任意一点E点（xE,yE）的挠度ωE。

当∂=00时为特殊状态下的直梁，积分路径则为沿x轴方向积分，其计算公式简化为：

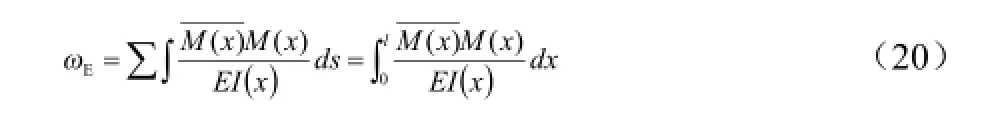
当∂=00时，积分路径则为沿x轴方向积分，也可依据材料力学中弯矩与挠度的微分关系，对q(x)进行积分，可得：

其中：C、D为常数。

将（13）、（17）公式以及实际的I(x)函数组合公式带入（21）公式中，再通过轻型卡车前后悬架与车架纵梁相互作用力简化成支撑纵梁支座后的边界条件。

以及奇异函数的积分公式（4）可形成一个奇异函数通用方程，求解车架纵梁上任意一点的挠度。

当∂=00、EI为常量时，上述公式（21）可进一步简化为：

其中，ω0、θ0可通过边界条件（22）式求出。

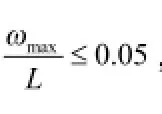
4、结束语

本文利用奇异函数，结合单位载荷法，针对轻型载货汽车常用的直纵梁、弯纵梁、变截面梁等车架纵梁，推导出通用的挠曲方程，克服了原来对变参数、变积分路径问题要进行分段求解的不足，并且求解过程规整，有利于编制程序，求解出最大挠度ωmax进行弯曲刚度校核，极大解决了人工计算的复杂性。

[1] 王燮山.奇异函数在力学中的应用[M].科学出版社,1993.

[2] 刘念超.奇异函数解几种超静定结构[J]．长沙交通学院学报. 1998.14(2)：20—25.

[3] 荆振华.奇异函数在材料力学中的应川[J].辽宁省交通高等专科学校学报,1997,5(1)：52—58.

[4] 俞德津.利用奇异函数法对专用汽车纵梁的强度分析[J].专用汽车.2003(5)，6—8.

[5] 曾纪鹏.用奇异函数建立变参数连续梁挠度统一方程的新方法[J].四川建筑,2010,31(1)：128～130.

[6] 徐彬.高层建筑结构分析的奇异甬数方法[D].华南理工大学,2000.

[7] 徐彬.奇异函数建立高层结构分析模型的方法及应用[J].昆明理大学学报,2000,25(6)：106～109.

[8] 王燮山.用奇异函数求解某些变形梁的变形[J].力学与实践,1984（4）：53～55.

[9] 李廉锟.结构力学[M].高等教育出版社，2004,97-99.

The bending stiffness analysis on the longitudinal beam of the light truck by using the singular function

Zuo Yingbo, Sun Jiangping, Cai Xin
( Anhui Jianghuai Automobile Co., Ltd, Anhui Hefei 230601）

By using the singular function and the unit load method,the deflection equation for the longitudinal beam of the light truck on the general stress state can be derived in this article.Then it can calculates the maximum deflection of the longitudinal beam by using the deflection equation for checking the bending stiffness.

Singular function; Longitudinal beam; Deflection curve equation; Unit load; Bending stiffness

U467.3

A

1671-7988 (2017)05-54-03

左印波（1986-），总布置工程师，就职于安徽江淮汽车集团股份有限公司，技术中心轻型商用车研究院，主要研究方向为整车总布置。

10.16638/j.cnki.1671-7988.2017.05.018