风帆助航船舶直线航迹跟踪的自适应非线性迭代滑模控制

沈智鹏， 张晓玲

(大连海事大学 信息科学技术学院，辽宁 大连 116026)

随着全球海上经济贸易不断发展和人们的环保意识不断增强，如何节省航行时间、节能减排和缩短航程逐渐成为人们研究的重点，风帆助航船舶因具有风力辅助推进的特点而受到广泛关注。文献[1]为风帆助航船舶建立四自由度的数学模型并进行仿真试验。结果表明，在引入风帆之后，船舶航速得到提升，但船舶运动的不确定性、时变性和非线性增强，并使船舶的偏航增加。因此，为保障船舶航行时的安全性和经济性，有必要对船舶直线航迹跟踪控制器进行研究。

近年来，随着船舶航迹控制不断发展，出现多种解决系统的不确定性问题的方法。文献[2]采用重新定义输出变量的思想，克服转艏角速度不能为零、无法保证新定义的输出变量的收敛性的局限，提出一种状态反馈控制律，但并未对系统的全局渐进稳定性进行充分性证明。为改进控制律，文献[3]～文献[5]在文献[2]的基础上重新定义输出变量，得到全局渐进稳定性的充分条件，获取更好的控制律，并给出参数设置的方法。文献[5]采用无源化和Backstepping级联的方法设计船舶直线航迹控制器。文献[6]针对气垫船设计一种结合微分单调性和高阶滑模控制的二阶航迹控制器，获得平滑的控制效果和更强的鲁棒性。文献[8]采用输出反馈的方法设计航迹跟踪控制器，并建立1∶70的微缩模型进行仿真试验。文献[9]～文献[11]采用滑模控制法设计船舶航迹跟踪控制器，并从理论的角度证明其有效性。

随着船舶运动控制不断发展，智能控制逐渐被应用到船舶运动控制领域中。文献[11] 在将直线航迹控制数学模型转化为确定的非线性系统之后提出Backstepping自适应模糊控制器，并证明其稳定性。文献[12]采用RBF神经网络的方法逼近船舶不确定项及非线性部分，建立一种基于Serret-Frenet框架的神经滑模船舶运动控制器。虽然上述方法对船舶运动控制有效，但处理方法较为复杂，难以应用到风帆助航船舶等时变非线性系统中。文献[13]采用复杂度较低的线性递归滑模方法获取控制量的递推算法，然而该方法需对模型控制增益进行线性化处理，不能直接应用到复杂的非线性船舶模型中。文献[14]采用递归线性滑模的方式获取控制量的递推算法，计算的复杂度相对较低，但需对模型控制增益进行线性化处理。文献[15]～文献[17]采用非线性滑模法对船舶、UUV和AUV进行运动控制，不仅能避免对模型进行线性化处理，还可避免对模型中的不确定量及外界扰动量进行估计，但该控制器滑模参数固定不变，无法确保控制器在任意时刻取得最优值，缺乏自适应能力。

考虑到船舶的横向漂移及船舶模型的不确定性，为确定舵角来控制船舶航向，间接达到航迹跟踪控制的目的，以风帆助航船舶的直线航迹跟踪控制为目标，结合文献[14]～文献[16]，提出并建立一种基于自适应启发评价[17-18]的模糊迭代滑模控制器。这种控制方法无需对模型的不确定项和外部干扰项进行估计，可避免对模型进行线性化处理，且滑模面构造相对简单。为获得相对良好的控制效果，增强控制器的自适应能力，采用文献[17]中的模糊逻辑推理方法调节控制器参数，并基于文献[18]中的评价函数对输出结果进行反馈评价，根据评价结果对模糊系统中的参数进行适当的调节。此外，以散货船“文竹海”号为目标，设计基于自适应启发评价的模糊迭代滑模控制器，根据李雅普诺夫稳定性理论分析证明其稳定性，在风、浪等干扰环境下进行船舶航迹直线跟踪控制仿真，并将仿真结果与迭代滑模控制器相对比。

1 风帆助航船舶运动数学模型

基于MMG分离模型思想[19]，结合文献[20]中的四自由度帆船模型，将风帆助航船舶运动惯性数学模型描述为

(1)

式(1)中：X和Y分别为船舶在X方向及Y方向上所受的力；N为艏摇力矩；L为横摇力矩；H，P，R，wind，wave，S分别为裸船体、螺旋桨、舵、风、波浪及风帆；u为纵荡速度；v为横荡速度；r为艏摇角速度；p为横摇角速度；x和y为船舶重心在固定坐标系下的位置；Ψ为航向角；uc为水流的速度；Ψc为水流的角度；m为船舶质量；mx和my分别为附体坐标系下x轴及y轴的附加水质量；Jxx为附体坐标系下x轴的附加转动惯量；Jzz为附体坐标系下z轴的附加转动惯量；Ixx为附体坐标系下x轴的转动惯量；Izz为附体坐标系下y轴的转动惯量。

在实际的船舶操纵过程中，仅使用舵来控制船舶的航迹。受船舶自身特性的限制，在船舶航行过程中，常规船舶的舵角通常<35°，最大转艏角速度通常为0.01～0.02 rad/s。

2 风帆助航船舶直线航迹跟踪控制器设计

对于欠驱动船舶而言，仅能通过舵来控制航向和航迹，需通过确定控制舵角达到直线航迹跟踪的目的。通过坐标系旋转和平移，将控制目标转化为确定的命令舵角，使船舶的直线航迹偏差ye→0，若不存在风、浪、流的干扰，则还有航向偏差φe→0(期望航向即给定的直线航迹方向)。

2.1 非线性迭代滑模控制器的设计

由于风帆助航船舶相比普通船舶更易受到外界风的干扰，因而其模型的非线性和不确定性有明显增加。为获得更好的控制效果，可采用非线性迭代滑动模态设计方法，将系统的控制目标转化为对零阶系统s4的控制问题，即

(2)

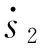
(3)

式(3)中：ks和ε∈R+。

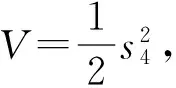
(4)

式(4)中：s4的展开式为

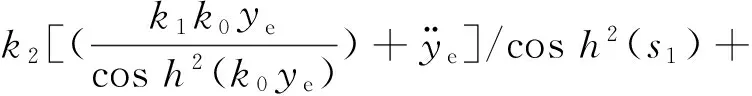
(5)

NR=h(x)cosδsinαR

(6)

式(6)中：αR为有效冲角，大小与舵角输入δ有关且符号与其相同；h(x)为一个恒正的函数。综上可知，NR对δ求导在δ∈(-35°,35°)上是恒大于零的。同理，可证明XR和YR在δ∈(-35°,35°)上是恒大于零的。

对式(5)两边关于δ求导，展开后可得

(7)

(8)

综合式(4)、式(7)和式(8)可知，必然存在一组数值k0～k4使得

(9)

由Lyapunov稳定性定理可知，在式(3)的作用下，系统是渐近稳定的。

2.2 控制器参数的模糊优化

为缓解控制量输出波动带来的机械损伤，延长舵机的使用寿命，减小输出抖振是十分必要的。由式(3)中参数的特性可知，系统控制性能与滑模面反馈控制参数ks有关。若能根据实际测量的抖振变量值在线调整结构参数，从而实现模糊规则和结构参数的动态调整，则能减小舵的抖振，达到延长设备使用寿命的目的。虽然所设计的迭代滑模控制器对船舶航迹控制有良好的效果，但由于控制器参数为恒值，无法随环境的变化而改变，因而无法完全满足控制需求。对此，基于上述优化设计思想，设计图1所示的控制器结构框图。

2.2.1控制参数模糊系统设计

由式(3)可知，系统的控制品质和鲁棒性受滑模反馈控制增益参数ks的影响。在配置参数时，控制增益过大易使控制量产生抖振，而控制增益过小又会使跟踪性能变差。因此，可利用模糊逻辑系统对反馈控制增益ks进行自适应优化调节。

(10)

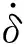
(11)

2.2.2控制参数优化

由于模糊逻辑推理本身对系统参数有良好的调节作用，因此在参数适合的情况下该控制器能有效抑制系统的抖振。然而，模糊逻辑推理系统的取值范围大多依靠设计者的个人经验界定，且需经过反复的试验验证，实现起来相对较为繁琐。因此，设计者通常使用的静态模糊规则和模糊隶属函数很难达到预想的设计效果。

为对参数进行评价和优化，借鉴文献[18]中的强化学习思想，通过定义一个启发评价函数对模糊系统输出误差进行评价，评价控制增益的优化效果，根据评价结果推导出模糊规则和结构参数自适应在线调整律，从而实现模糊规则和结构参数的动态调整，进一步优化控制增益参数，达到优化控制器参数的目的。

(12)

式(12)中：E为控制器输出误差；d为模糊输出的目标值，d∈R。显然，d的大小无法预先确定，但可通过引入评价参数γk间接得到与ks和d的关系，即

(13)

(14)

式(14)中：T为仿真时间；ρk(l)的表达式为

(15)

在系统输出产生抖振时，输出的变化趋势会不停地发生改变。式(15)中的ρk(l)当且仅当舵角改变变化趋势时记为1，否则记为0。因此，结合式(14)即可描述最近50个周期内系统输出的抖振变化情况。

综合上述算式可知，评价参数γk仅反映抖振的变化趋势，并不会对模糊系统产生影响，因此可用于衡量输出误差。在模糊系统的自适应调解中，设计者仅需得知抖振的变化趋势。

(16)

式(16)中：α为学习步长；zj为第j条规则在此时的隶属函数。由于模糊系统采用的高斯隶属函数是可微分的，因此式(16)中偏导数是恒存在的，在线调整率成立。

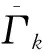
3 仿真研究

以载重量76 000 t远洋散货船“文竹海”号为研究对象，建立风帆助航船舶模型并设计控制器。船舶主要参数见表1。

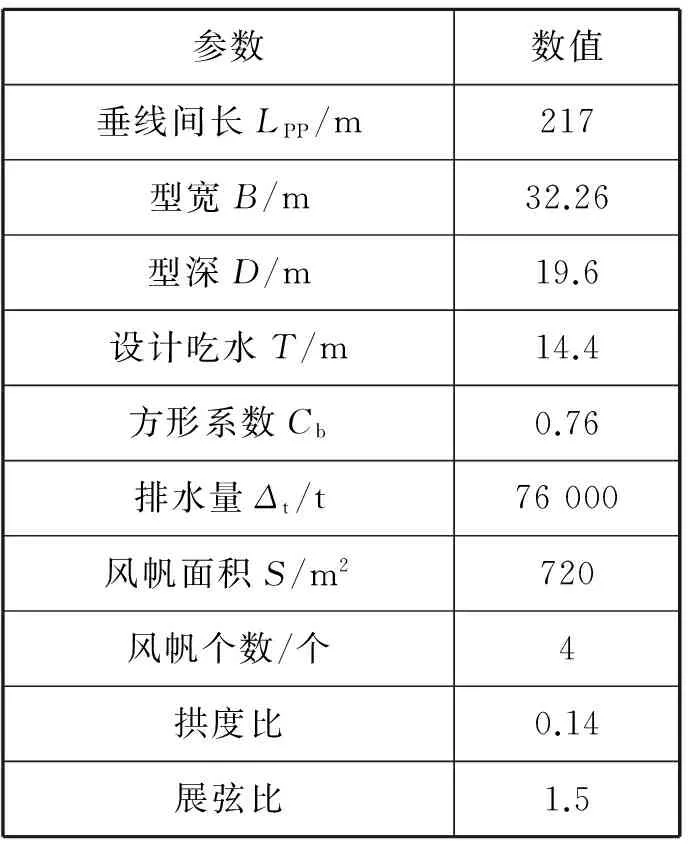
表1 船舶主要参数

假设流力和流向在船舶航行过程中为定值，风级为4～8级，风帆角始终处于最佳攻角状态(即风帆最大推力状态)。

图2～图7分别为风帆助航船舶在设定环境和设定工况下的运动航迹、舵角及控制器部分参数的变化曲线。由图2可知，在添加自适应启发评价系统之后，风帆助航船舶到达目标航迹的时间有一定的减少。由图3可知，受外力干扰，船舶航向无法保持为一个定值。在使用自启发评价控制之后，控制速度的增加使得航向变化相对较为剧烈。由图4可知，2种控制器的舵角均在10°左右，且舵角变化曲线相近。因此，自适应启发评价控制器在直线航迹跟踪运动中可使船舶快速、安全地到达目标航迹。由图5和图6可知，评价函数确实对模糊系统参数及控制器参数ks存在调节作用，算法有效，主要调节效果可由图7得知。由图7可知，相较于迭代滑模控制器，本文设计的控制器输出抖振相对较小，故该控制器有效。

4 结束语

本文基于自适应启发评价的模糊迭代滑模控制方法，以风帆助航船舶运动控制系统为对象，设计一种船舶直线航迹控制器。该控制方法利用双曲正切函数的有界性，结合迭代滑模的控制方法，将船舶运动的控制问题转化为零阶镇定控制问题。该方法不仅能避免对模型未知项及不确定干扰项进行估计，还可利用外界扰动提高控制速率。为使控制器参数随控制量有规律地改变，引入模糊逻辑推理系统对控制器参数进行自适应调节。为使模糊逻辑推理系统更为合理，引入评价函数，合理地对模糊逻辑推理系统的参数进行评价和调节。由仿真结果可知，该控制器对风、浪等外界干扰具有较强的鲁棒性，且不会对船舶跟踪时间产生影响。同时，由舵角及航迹、航向的变化趋势可知，在不规则风、浪的干扰下，可使船舶以相对合理的舵角在目标航线上航行。综上，本文设计的控制器可在保证风帆助航船舶直线航迹跟踪性能的同时，使输出的信号更加符合实际船舶操纵要求，具有一定的工程意义和参考价值。

参考文献

[1] 沈智鹏, 姜仲昊. 风帆助航船舶运动模型[J]. 交通运输工程学报, 2015, 15(5):57-64.

[2] 李铁山, 杨盐生, 郑云峰. 不完全驱动船舶航迹控制输入输出线性化设计[J]. 系统工程与电子技术, 2004, 26(7):945-948.

[3] 周岗, 姚琼荟, 陈永冰,等. 基于输入输出线性化的船舶全局直线航迹控制[J]. 控制理论与应用, 2007, 24(1):117-121.

[4] 周岗, 陈永冰, 陈阳,等. 一种船舶直线航迹控制算法及控制参数的设计[J]. 仪器仪表学报, 2013, 34(5): 1043-1048.

[5] JIANG Z P. Global Tracking Control of Underactuated Ships by Lyapunov’s Direct Method[J]. Automatica, 2002, 38(2):301-309.

[6] SIRA-RAMIREZ H. Dynamic Second-Order Sliding Mode Control of the Hovercraft Vessel[J]. IEEE Transactions on Control Systems Technology, 2002, 10(6):860-865.

[7] 周岗, 姚琼荟, 陈永冰,等. 不完全驱动船舶直线航迹控制稳定性研究[J]. 自动化学报, 2007, 33(4):378-384.

[8] WONDERGEM M, LEFEBER E, PETTERSEN K Y, et al. Output Feedback Tracking of Ships [J]. IEEE Transactions on Control Systems Technology, 2011, 19(2):442-448.

[9] YU R, ZHU Q, XIA G, et al. Sliding Mode Tracking Control of an Underactuated Surface Vessel[J]. IET Control Theory & Applications, 2012, 6(3):461-466.

[10] ASHRAFIUON H, MUSKE K R, MCNINCH L C, et al. Sliding-Mode Tracking Control of Surface Vessels [J]. IEEE Transactions on Industrial Electronics, 2008, 55(11):4004-4012.

[11] 孟威, 郭晨, 孙富春, 等. 欠驱动水面船舶的非线性滑模轨迹跟踪控制[J]. 哈尔滨工程大学学报, 2012, 33(5): 585-589.

[12] 潘永平, 黄道平, 孙宗海. 欠驱动船舶航迹Backstepping自适应模糊控制[J]. 控制理论与应用, 2011, 28(7):907-914.

[13] HUANG Z, EDWARDS R M, LEE K Y. Fuzzy-Adapted Recursive Sliding-Mode Controller Design for a Nuclear Power Plant Control[J]. IEEE Transactions on Nuclear Science, 2004, 51(1):256-266.

[14] 卜仁祥, 刘正江, 李铁山. 船舶航迹迭代非线性滑模增量反馈控制算法[J]. 交通运输工程学报, 2006, 6(4):75-79.

[15] 边信黔, 程相勤, 贾鹤鸣, 等. 基于迭代滑模增量反馈的欠驱动 AUV 地形跟踪控制[J]. 控制与决策, 2011, 26(2): 289-292.

[16] 贾鹤鸣, 张利军, 程相勤, 等. 基于非线性迭代滑模的欠驱动 UUV 三维航迹跟踪控制[J]. 自动化学报, 2012, 38(2): 308-314.

[17] ERBATUR K, KAYNAK O. Use of Adaptive Fuzzy Systems in Parameter Tuning of Sliding-Mode Controllers[J]. IEEE/ASME Transactions on Mechatronics, 2001, 6(4):474-482.

[18] SHEN Zhipeng, GUO Chen, ZHANG Ning. A General Fuzzified CMAC Based Reinforcement Learning Control for Ship Steering Using Recursive Least-Squares Algorithm [J]. Neurocomputing, 2010, 73(4):700-706.

[19] 贾欣乐,杨盐生. 船舶运动数学模型: 机理建模与辩识建模[M]. 大连：大连海事大学出版社, 1999:49-138,294-349.

[20] LIN X, JOUFFROY J. Modeling and Nonlinear Heading Control for Sailing Yachts[J]. Oceans,2011,39(2):1-6.